iPAS AI應用規劃師 考試重點

L23304 模型調整與優化
主題分類
1
過擬合/欠擬合診斷
2
超參數調整基礎
3
常用調整策略
4
正則化技術
5
交叉驗證應用
6
優化演算法概念
7
模型評估與選擇
8
實務考量與工具
#1
★★★★★
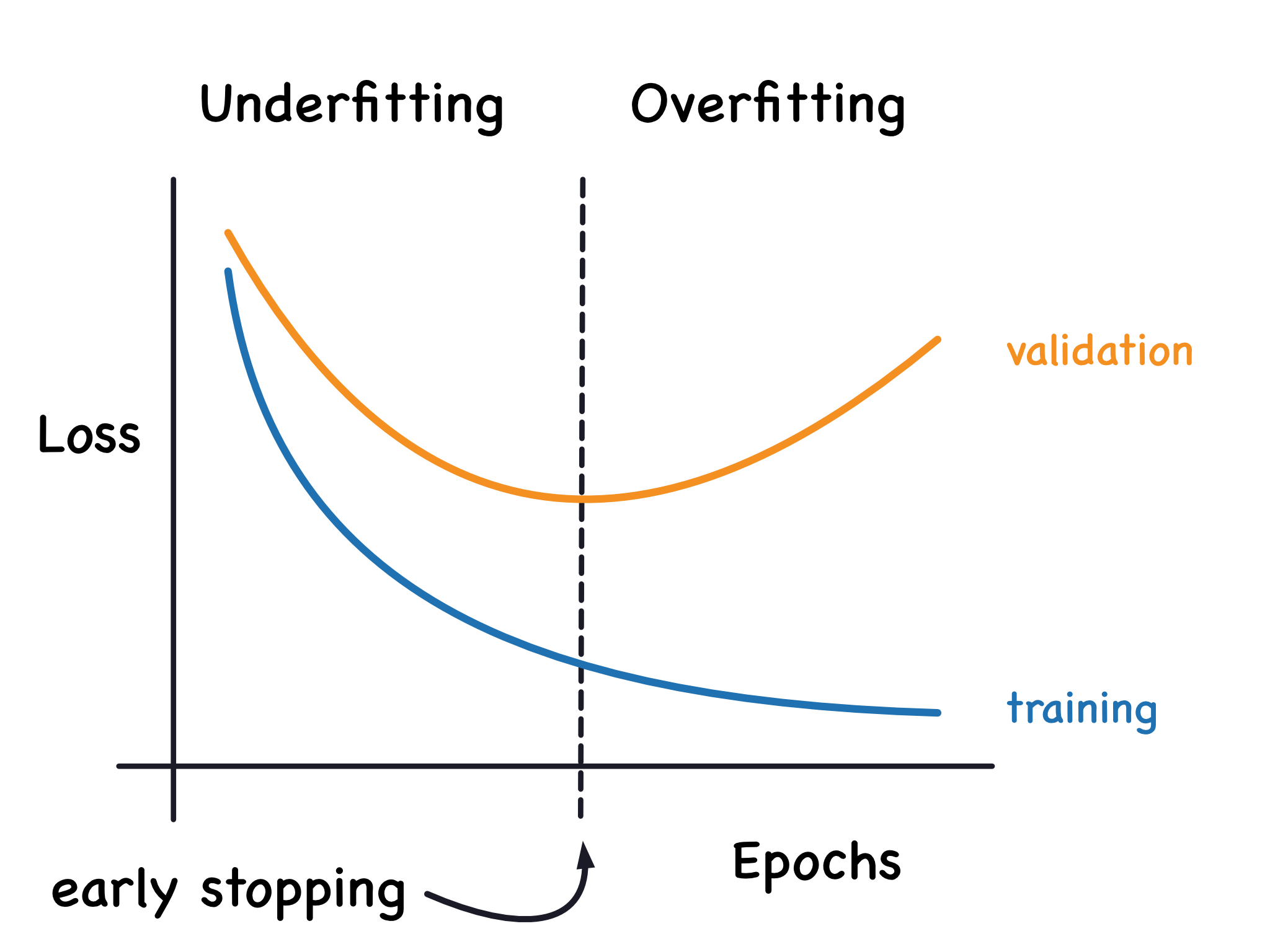
過擬合 (Overfitting) - 定義與特徵
核心概念
過擬合 指的是機器學習模型在訓練數據上表現極好，但在未見過的測試數據或新數據上表現很差的現象。模型過度學習了訓練數據中的噪聲和細節，導致其泛化能力 (Generalization Ability) 下降。特徵是訓練誤差低，但驗證/測試誤差高。(參考樣題 Q13)
#2
★★★★
欠擬合 (Underfitting) - 定義與特徵
核心概念
欠擬合 指的是模型過於簡單，無法捕捉數據中的基本模式和趨勢，導致在訓練數據和測試數據上表現都不佳。模型未能充分學習數據的複雜性。特徵是訓練誤差和驗證/測試誤差都很高。
#3
★★★★
診斷過擬合/ 欠擬合 - 學習曲線 (Learning Curves)
診斷方法
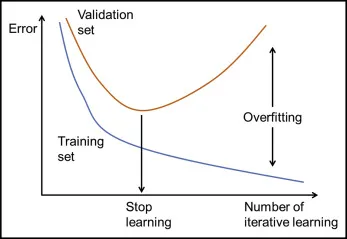
學習曲線 繪製了模型在訓練集和驗證集上的性能（如誤差或準確率）隨訓練樣本數量或訓練迭代次數變化的趨勢。
  • 過擬合：訓練曲線持續下降/上升，而驗證曲線在某點後開始停滯或惡化，兩者之間差距增大。
  • 欠擬合：訓練曲線和驗證曲線都收斂到較差的性能水平，且兩者差距不大。
觀察學習曲線有助於判斷模型狀態。
#4
★★★★★
解決過擬合的方法
常用策略
常見的解決過擬合的方法包括：
  • 增加訓練數據量。
  • 降低模型複雜度（例如，減少神經網路層數/單元數、降低多項式階數）。
  • 使用正則化 (Regularization) 技術（如 L1, L2）。(參考樣題 Q3)
  • 使用 Dropout（主要用於神經網路）。
  • 提早停止 (Early Stopping)。
  • 進行特徵選擇 (Feature Selection)。
  • 使用交叉驗證 (Cross-Validation) 進行評估和調優。(參考樣題 Q9)
#5
★★★★
解決欠擬合的方法
常用策略
常見的解決欠擬合的方法包括：
  • 增加模型複雜度（例如，增加神經網路層數/單元數、使用更高階的多項式特徵）。
  • 添加更多相關特徵 (Feature Engineering)。
  • 減少正則化強度。
  • 延長訓練時間（如果模型尚未收斂）。
  • 嘗試不同的模型架構或演算法。
#6
★★★★★
超參數 (Hyperparameter) vs. 模型參數 (Model Parameter)
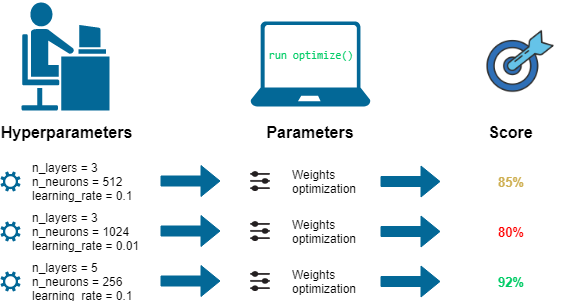
核心區別
  • 模型參數：模型內部的變數，其值是從訓練數據中學習得到的（例如，線性回歸的係數、神經網路的權重）。
  • 超參數：模型外部的配置變數，其值在學習過程開始之前設定，用於控制學習過程本身（例如，學習率、正則化強度、神經網路的層數、K-Means 中的 K 值）。
模型調整與優化主要針對超參數進行調整。
#7
★★★★
常見的超參數範例
舉例說明
不同模型的超參數不同，常見例子：
  • 神經網路：學習率 (Learning Rate)、隱藏層數量、每層單元數、激活函數、批次大小 (Batch Size)、訓練輪數 (Epochs)。
  • 支持向量機 (SVM)：核函數 (Kernel)、懲罰參數 C、核係數 gamma。
  • 決策樹/隨機森林：樹的最大深度、節點分裂的最小樣本數、森林中的樹木數量。
  • 正則化：正則化強度參數（如 L1 的 alpha, L2 的 lambda）。
#8
★★★★★
超參數調整 (Hyperparameter Tuning / Optimization) 的目標
核心目標
目標是找到一組最佳的超參數組合，使得模型在未見過的數據上（通常透過驗證集評估）達到最佳性能（根據選擇的評估指標，如準確率、F1 分數、均方根誤差等）。這有助於提高模型的泛化能力。
#9
★★★★
調整策略：手動調整 (Manual Search)
方法說明
基於經驗、直覺或試誤法 (Trial and Error)，手動選擇和調整超參數。
  • 優點：可以利用領域知識和經驗。
  • 缺點：耗時、效率低、難以系統性探索、結果可能非最優、依賴專家經驗。(參考樣題 Q5 提到此方法趨勢下降)
#10
★★★★★
調整策略：網格搜尋 (Grid Search)
方法說明
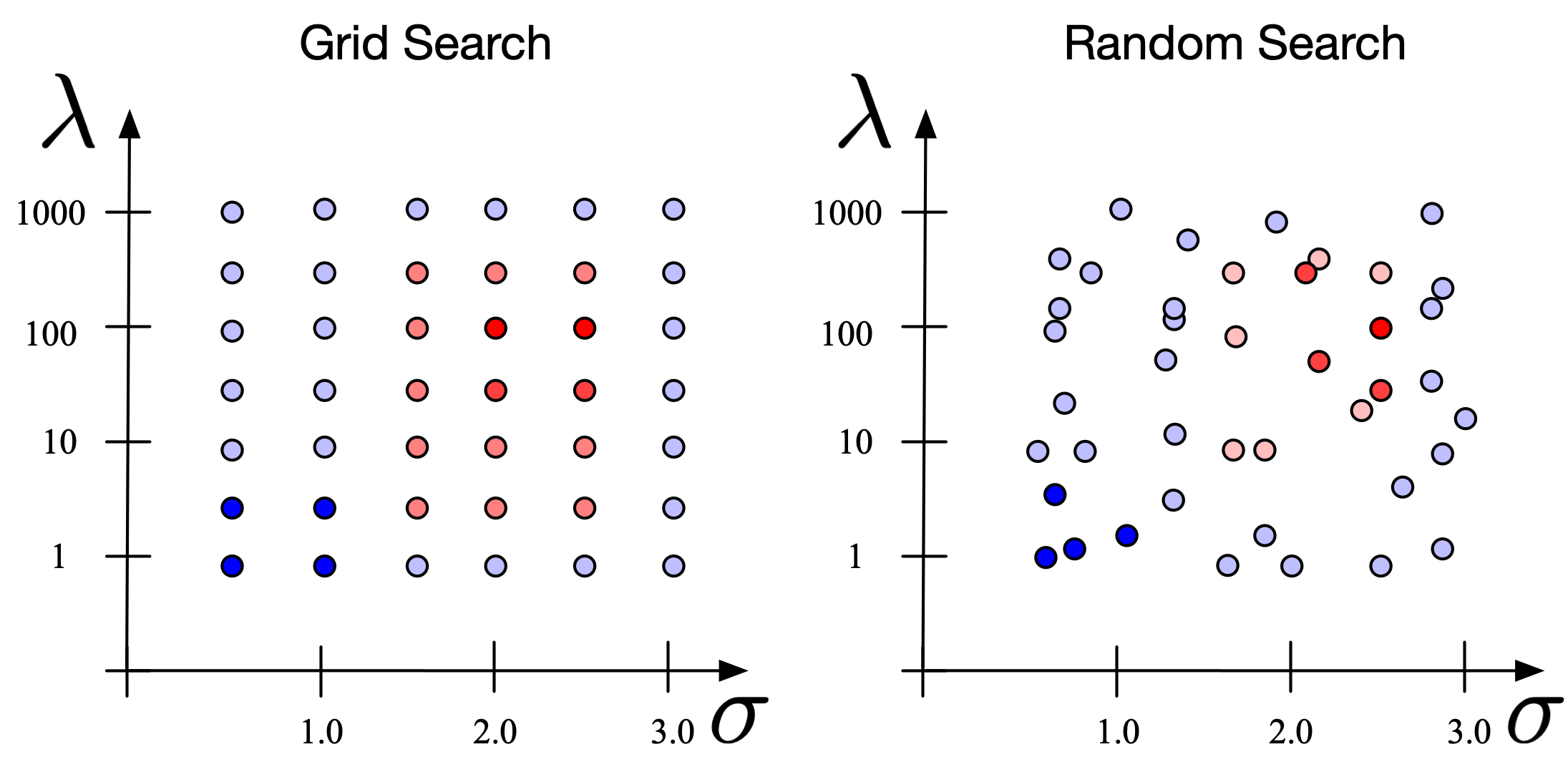
系統性地嘗試預先定義好的超參數範圍內的所有可能組合。
  • 優點：簡單、易於實現、保證找到指定網格內的最優組合。
  • 缺點：計算成本高，尤其當超參數數量多或範圍大時，會發生維度災難 (Curse of Dimensionality)。可能錯過網格點之間的最佳值。
#11
★★★★★
調整策略：隨機搜尋 (Random Search)
方法說明
在預先定義好的超參數範圍內隨機抽樣組合進行嘗試，通常會設定嘗試的次數。
  • 優點：比網格搜尋更有效率，特別是當只有少數超參數對模型性能影響較大時，更有可能找到接近最優的組合。
  • 缺點：結果具有隨機性，不保證找到全局最優解。
#12
★★★★
調整策略：貝氏優化 (Bayesian Optimization)
方法說明
一種基於機率模型（通常是高斯過程）的優化方法。它會根據先前的評估結果來建立目標函數的代理模型，並使用獲取函數 (Acquisition Function) 來智能地選擇下一個最有潛力的超參數組合進行評估。
  • 優點：通常比網格搜尋和隨機搜尋需要更少的評估次數就能找到好的解，特別適用於評估成本高的情況。
  • 缺點：實現相對複雜，對於高維度超參數空間可能效果下降。
#13
★★★
調整策略：基於梯度的方法 (Gradient-based Optimization)
方法說明
對於某些可微分的超參數（例如神經網路中的某些參數），可以嘗試使用基於梯度的方法進行優化。這通常需要對優化過程有更深入的理解和修改。
#14
★★★
調整策略：演化演算法 (Evolutionary Algorithms)
方法說明
模擬生物演化過程（如遺傳演算法），維護一個超參數組合的「族群」，透過選擇、交叉和變異等操作來迭代地產生更好的解。適用於複雜的非凸優化問題。
#15
★★★★★
正則化 (Regularization) - 目的與原理
核心概念
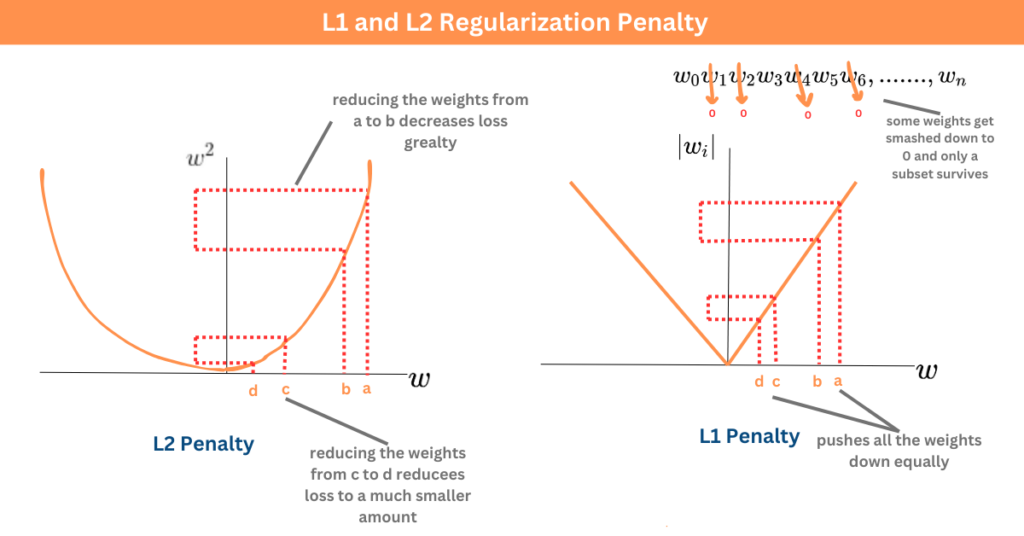
正則化 是一種用於防止模型過擬合的技術。其原理是在模型的損失函數 (Loss Function) 中加入一個懲罰項 (Penalty Term)，該懲罰項與模型參數的大小有關。這會限制模型參數的複雜度，使得模型不會過度擬合訓練數據。(參考樣題 Q3)
#16
★★★★★
L1 正則化 (Lasso Regression)
技術說明
懲罰項是模型參數絕對值之和（L1 範數）。
特點：傾向於產生稀疏解 (Sparse Solution)，即將某些不重要的特徵對應的參數縮減為零。因此，L1 正則化也可用於特徵選擇。
懲罰項形式： α * Σ|wᵢ| (α 或 λ 是正則化強度超參數)
#17
★★★★★
L2 正則化 (Ridge Regression)
技術說明
懲罰項是模型參數平方和之和（L2 範數的平方）。
特點：傾向於使所有參數都縮小，但通常不會變為零。對於處理共線性 (Collinearity) 問題（特徵之間高度相關）有幫助。在深度學習中也稱為權重衰減 (Weight Decay)。
懲罰項形式： α * Σ(wᵢ²) (α 或 λ 是正則化強度超參數)
#18
★★★
彈性網路 (Elastic Net)
技術說明
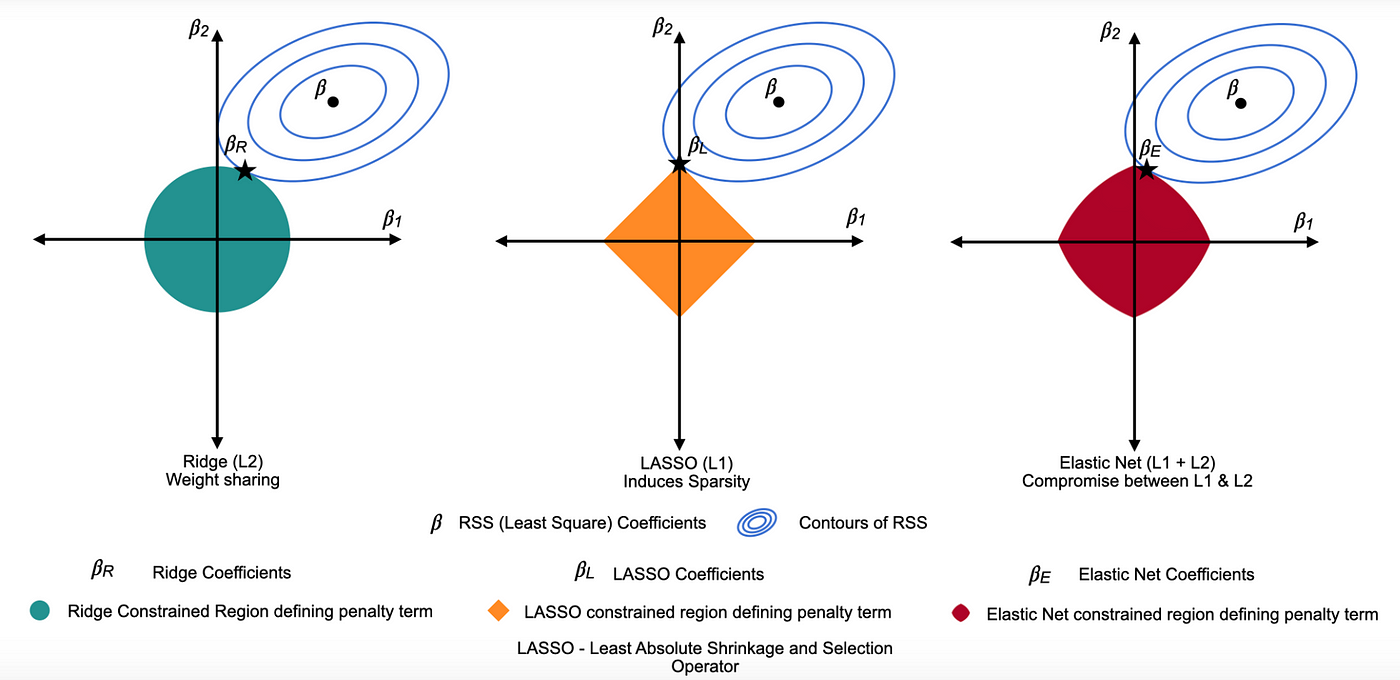
結合了 L1 和 L2 正則化的懲罰項。試圖兼具 L1 的稀疏性和 L2 的穩定性，尤其在特徵數量多於樣本數量或特徵之間存在高度相關性時可能表現更好。
懲罰項形式： α * [ ρ * Σ|wᵢ| + (1-ρ)/2 * Σ(wᵢ²) ] (α 控制總體強度，ρ 控制 L1 和 L2 的比例)
#19
★★★★
Dropout
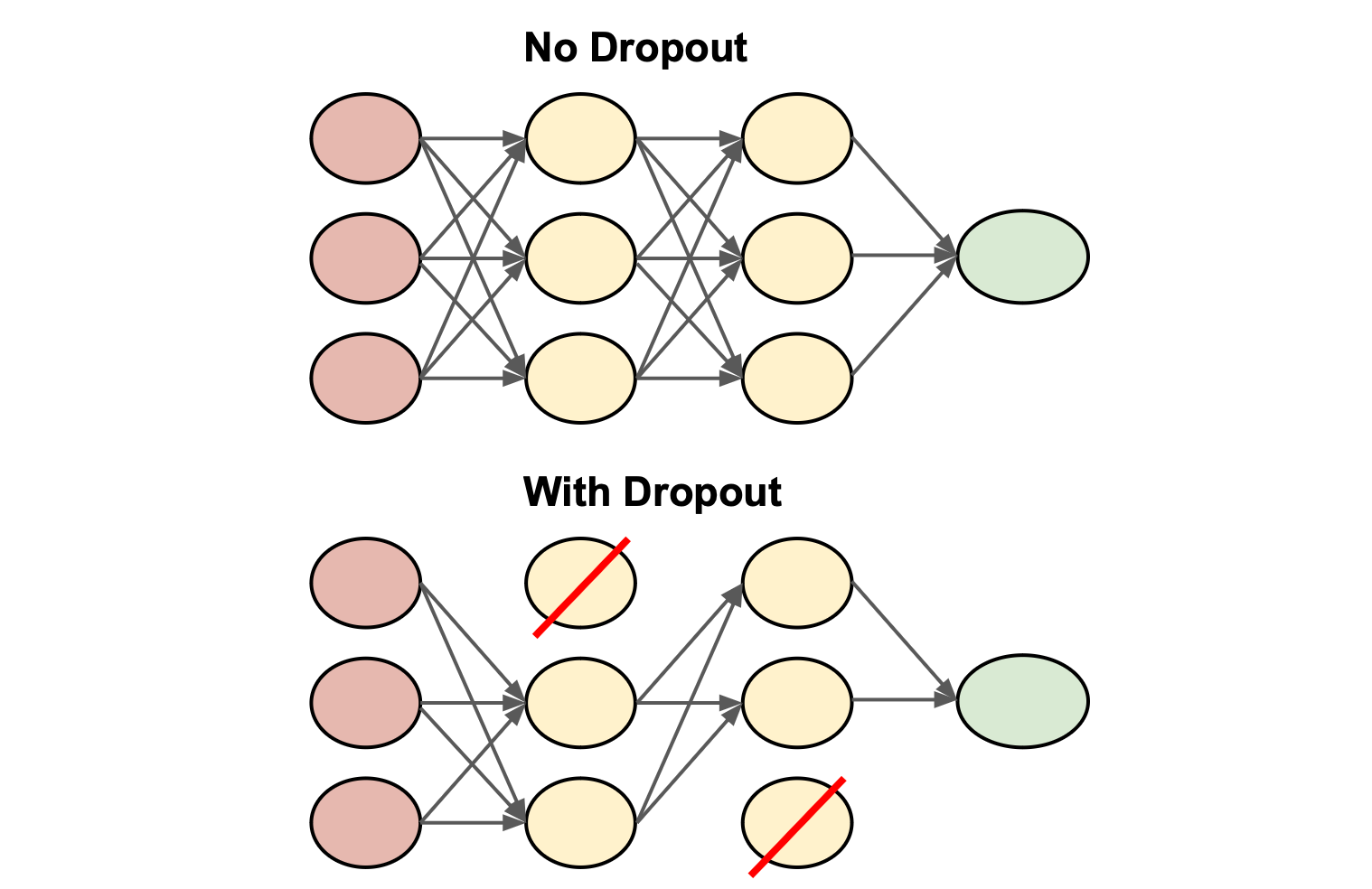
技術說明 (主要用於神經網路)
在神經網路訓練過程中，每次迭代隨機地「丟棄」（暫時移除）一部分神經元及其連接。這強迫網路學習更穩健的特徵，減少神經元之間的共適應 (Co-adaptation)，從而降低過擬合風險。Dropout 比率是一個超參數。
#20
★★★★
提早停止 (Early Stopping)
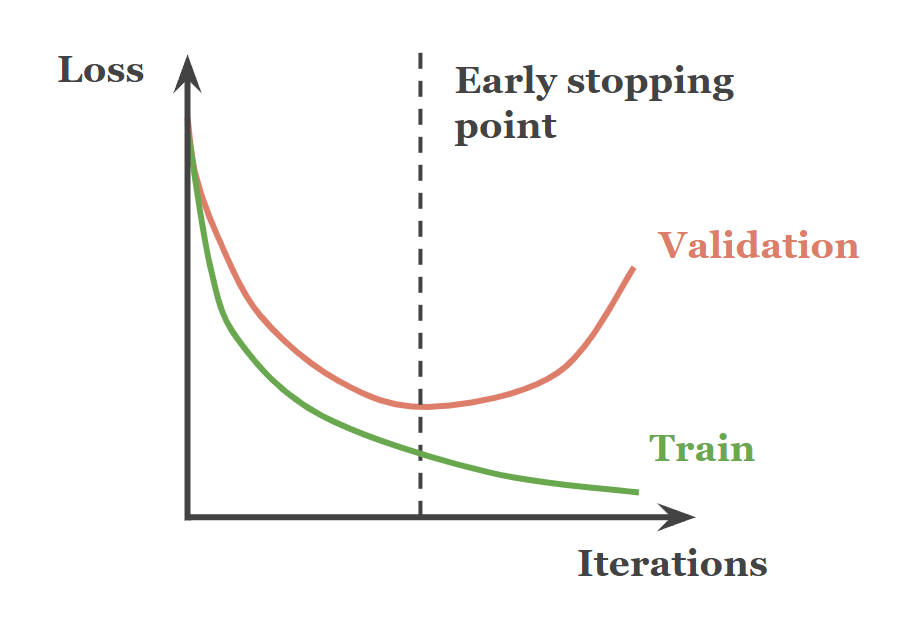
技術說明
在模型訓練過程中，監控模型在驗證集上的性能。當驗證集上的性能不再提升或開始下降時，就停止訓練，並保存性能最佳時的模型參數。這是一種簡單有效的防止過擬合的方法。
#21
★★★★★
交叉驗證 (Cross-Validation, CV) - 目的
核心目的
交叉驗證 的主要目的是更可靠地評估模型的泛化能力，並減少模型評估結果對特定數據劃分方式的依賴。它有助於：
  • 獲得對模型在未見數據上表現的更穩定、更無偏的估計。
  • 輔助超參數調整，選擇泛化能力最好的超參數組合。
  • 降低過擬合風險，避免模型僅在特定驗證集上表現良好。(參考樣題 Q9)
#22
★★★★★
K-摺交叉驗證 (K-Fold Cross-Validation)
方法說明
最常用的交叉驗證方法：
  1. 將原始訓練數據隨機劃分為 K 個大小相似的互斥子集（稱為「摺」，Fold）。
  2. 進行 K 次迭代：每次迭代選擇其中一摺作為驗證集，其餘 K-1 摺作為訓練集。
  3. 在 K-1 摺上訓練模型，並在選定的驗證摺上評估性能。
  4. 將 K 次迭代的性能指標（如誤差、準確率）平均，作為模型最終的性能評估結果。
常見的 K 值為 5 或 10。
#23
★★★
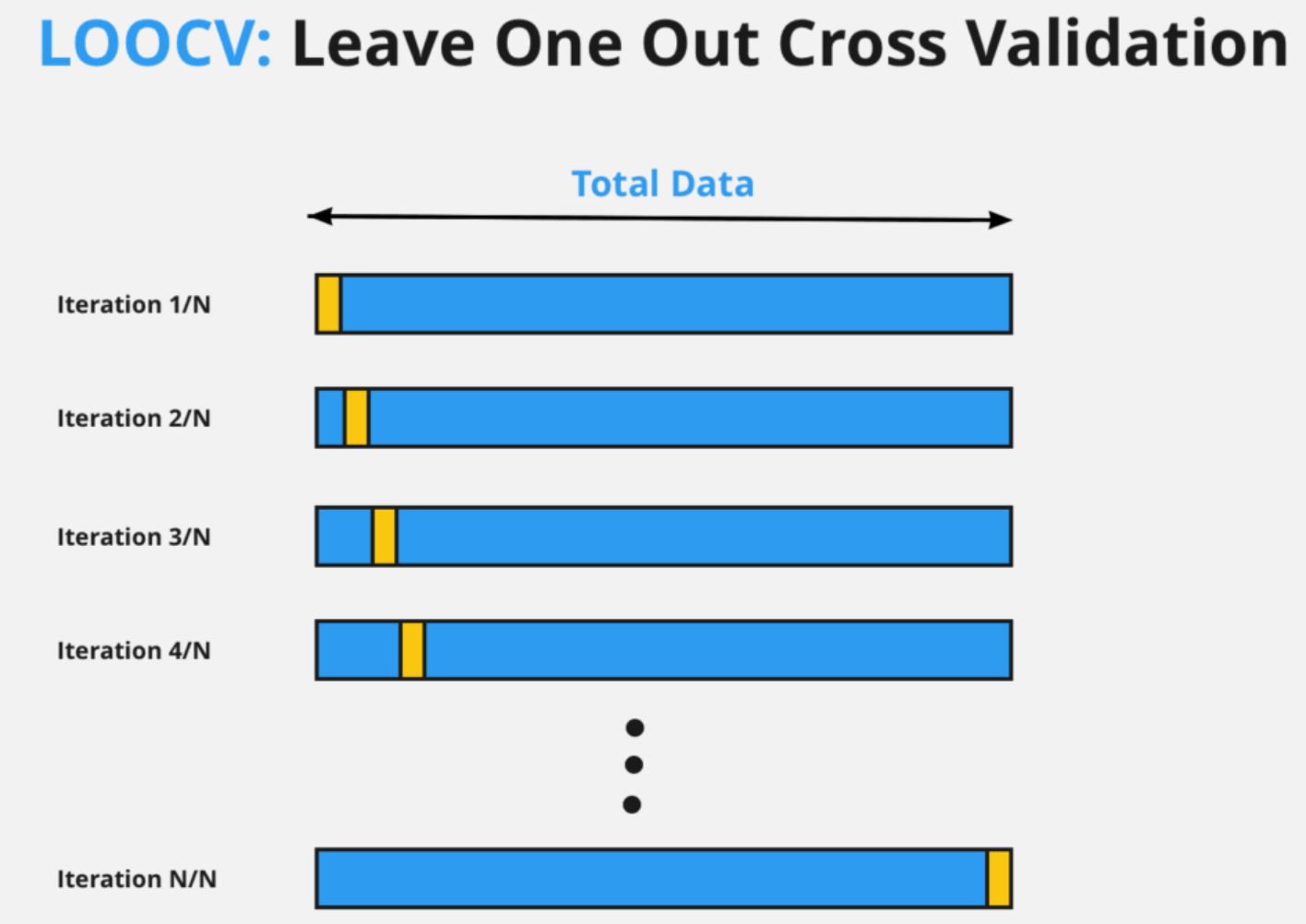
留一法交叉驗證 (LOOCV, Leave-One-Out Cross-Validation)
方法說明
K-摺交叉驗證 的特例，其中 K 等於樣本總數 N。每次迭代只留下一個樣本作為驗證集，其餘 N-1 個樣本用於訓練。
  • 優點：評估結果通常偏差較小，充分利用了數據。
  • 缺點：計算成本非常高，需要訓練 N 個模型。評估結果的變異數可能較大。
#24
★★★★
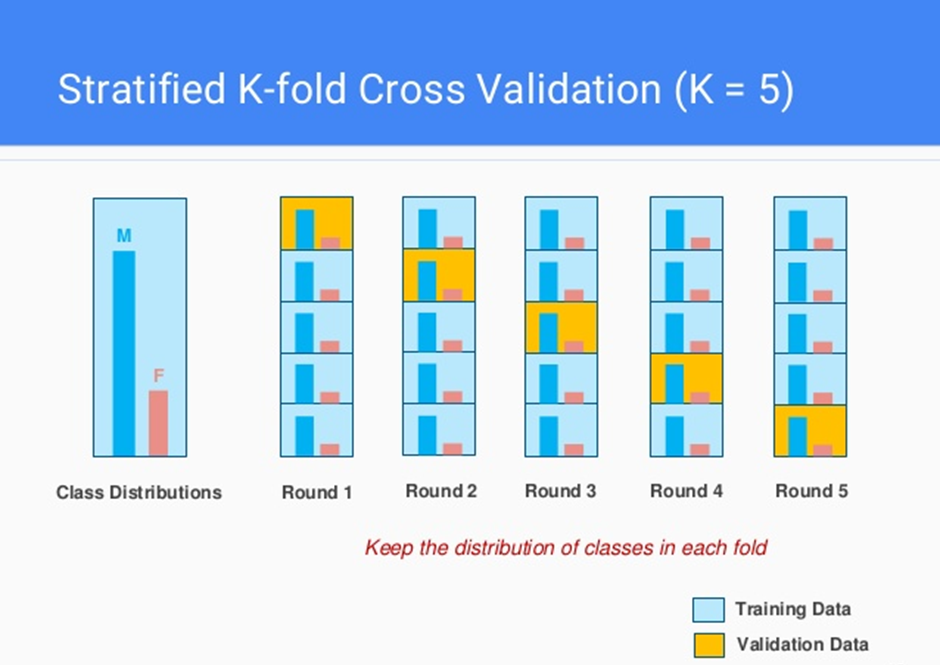
分層 K-摺交叉驗證 (Stratified K-Fold Cross-Validation)
方法說明
在進行 K-摺劃分時，確保每個摺中的類別比例（對於分類問題）與原始數據集中的類別比例大致相同。
特別適用於類別不平衡 (Imbalanced Classes) 的數據集，可以避免因隨機劃分導致某些摺中缺少少數類別樣本，從而得到更可靠的評估結果。
#25
★★★
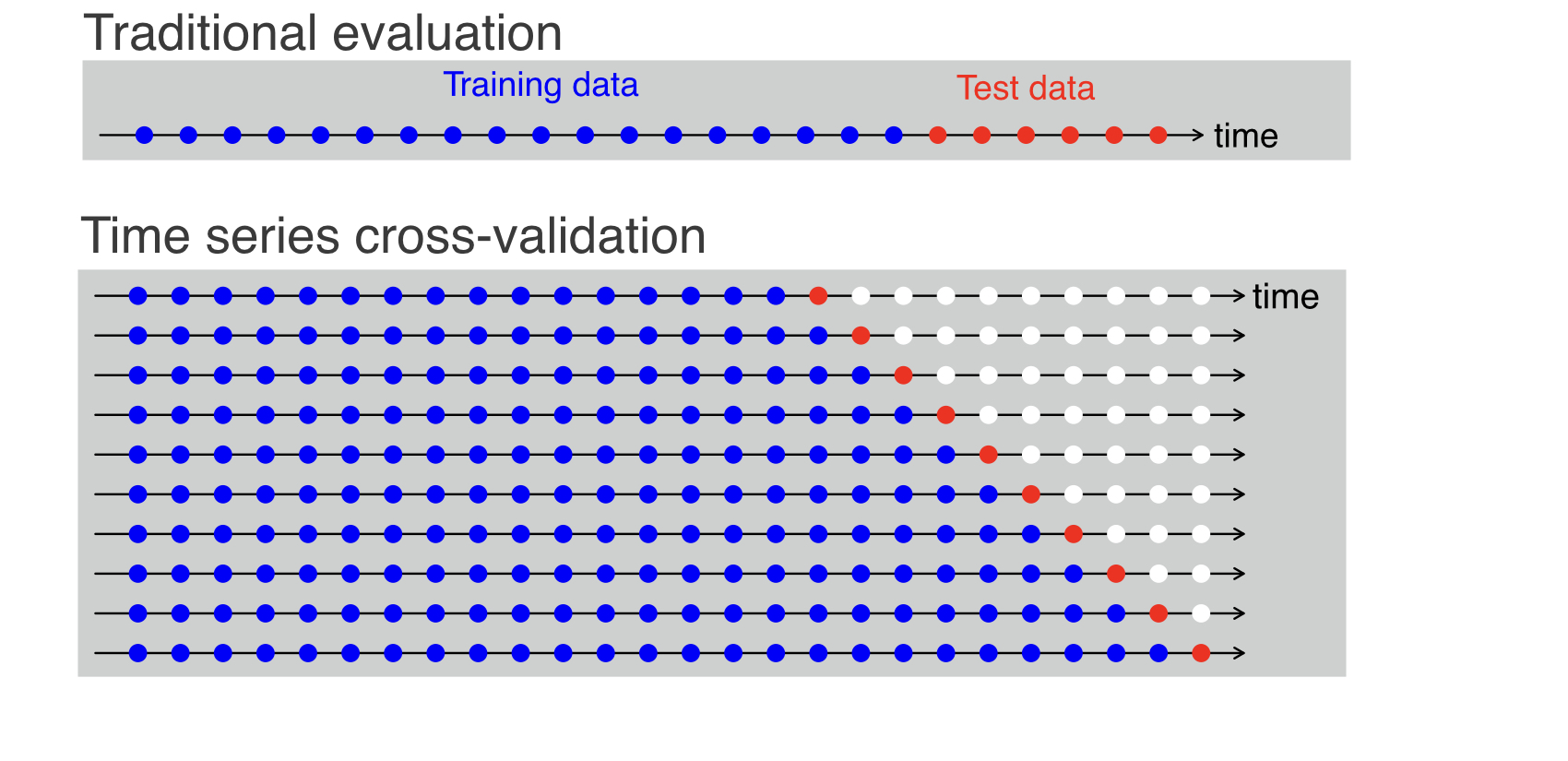
時間序列交叉驗證 (Time Series Cross-Validation)
方法說明
對於具有時間順序的數據（例如股價預測、氣象預報），不能使用標準的 K-摺交叉驗證（因為會打亂時間順序，導致用未來數據預測過去）。
常用的方法是滾動預測 (Rolling Forecast Origin) 或類似的向前驗證 (Forward Chaining) 策略：使用過去的數據訓練，預測緊鄰的未來數據點，然後將該數據點納入訓練集，繼續預測下一個點。
#26
★★★★
交叉驗證 在 超參數調整 中的應用
應用流程
將超參數調整策略（如網格搜尋、隨機搜尋）與交叉驗證結合使用：
  1. 對於每一組候選的超參數組合：
  2. 使用 K-摺交叉驗證 在原始訓練集上評估該組合的性能（得到 K 個性能指標，取平均）。
  3. 根據交叉驗證的平均性能，選擇表現最好的超參數組合。
  4. 最後，使用選定的最佳超參數，在整個原始訓練集上重新訓練最終模型。
這樣選出的超參數具有更好的泛化能力。
#27
★★★
優化演算法 (Optimization Algorithms) - 基本概念
核心目標
在機器學習中，優化演算法 用於調整模型參數（而非超參數），以最小化（或最大化）損失函數（或目標函數）。模型調整與優化雖然主要指超參數調整，但理解背後的參數優化過程有助於整體把握。
#28
★★★★
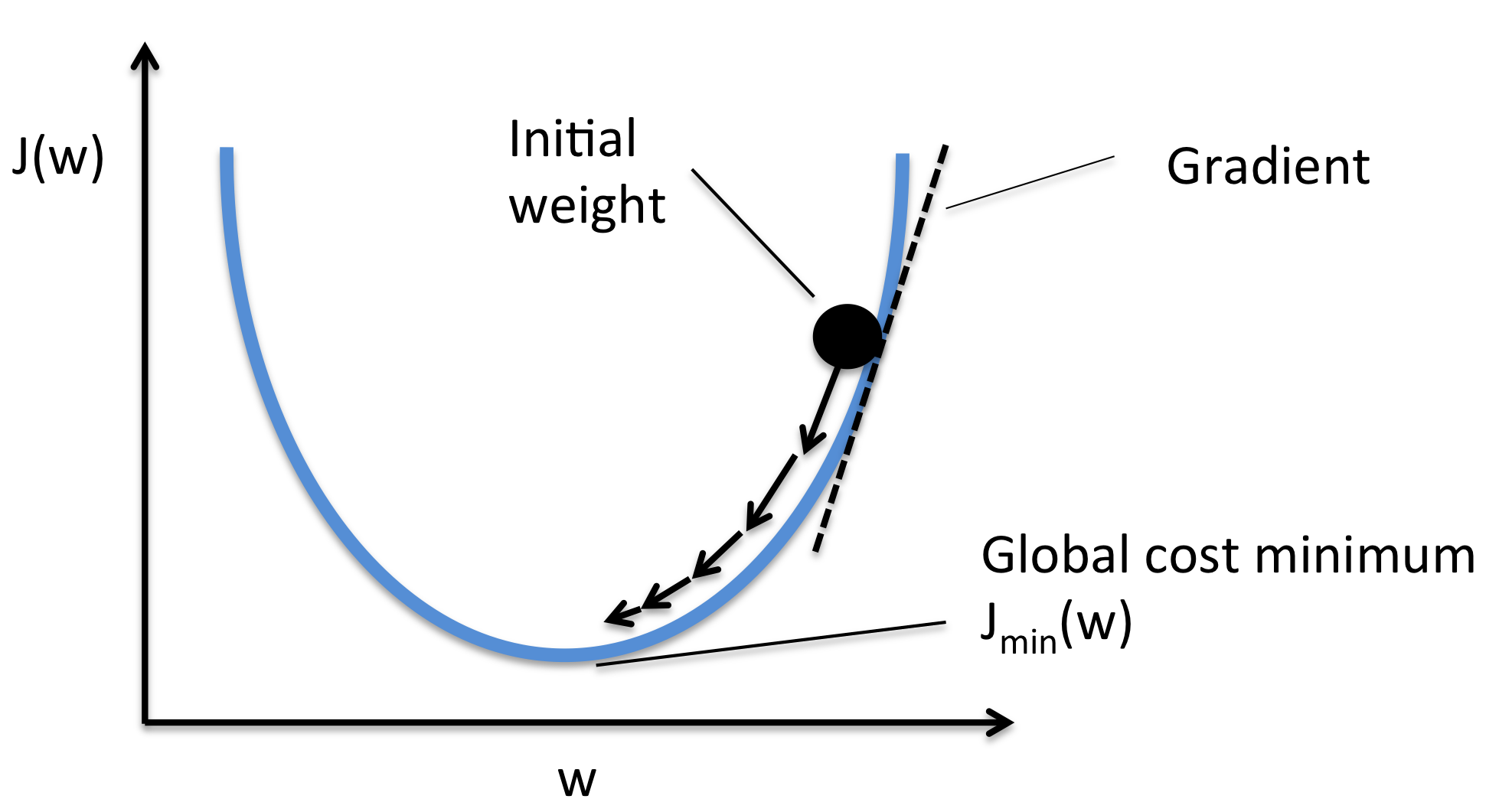
梯度下降法 (Gradient Descent)
核心演算法
最常用的優化演算法之一。其基本思想是：計算損失函數對模型參數的梯度（導數），然後沿著梯度的負方向（下降最快的方向）更新參數，步長由學習率 (Learning Rate) 控制。
Wnew = Wold - η * ∇Loss(Wold) (η 是學習率)
#29
★★★
隨機梯度下降法 (SGD, Stochastic Gradient Descent)
演算法變體
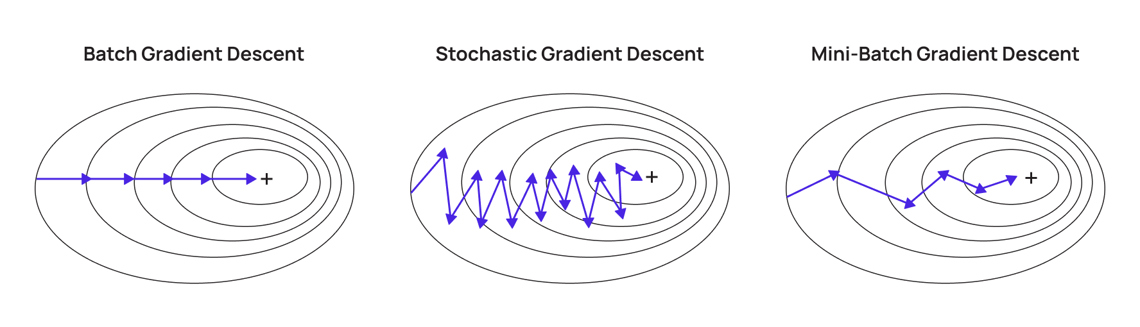
與標準梯度下降（計算整個訓練集的梯度）不同，SGD 每次迭代僅使用一個訓練樣本來計算梯度並更新參數。
  • 優點：計算速度快，適用於大規模數據集，更新頻繁有助於跳出局部最優點。
  • 缺點：梯度估計噪聲大，收斂過程可能震盪。
#30
★★★
小批量梯度下降法 (Mini-batch Gradient Descent)
演算法變體
介於標準梯度下降和 SGD 之間，每次迭代使用一小批 (Mini-batch) 訓練樣本來計算梯度並更新參數。
  • 優點：結合了兩者的優點，計算效率較高，收斂過程相對 SGD 更穩定，且能利用硬體並行計算。
  • 是目前最常用的梯度下降變體。
批次大小 (Batch Size) 是一個重要的超參數。
#31
★★★
帶有動量的優化器 (Optimizers with Momentum)
改進方法
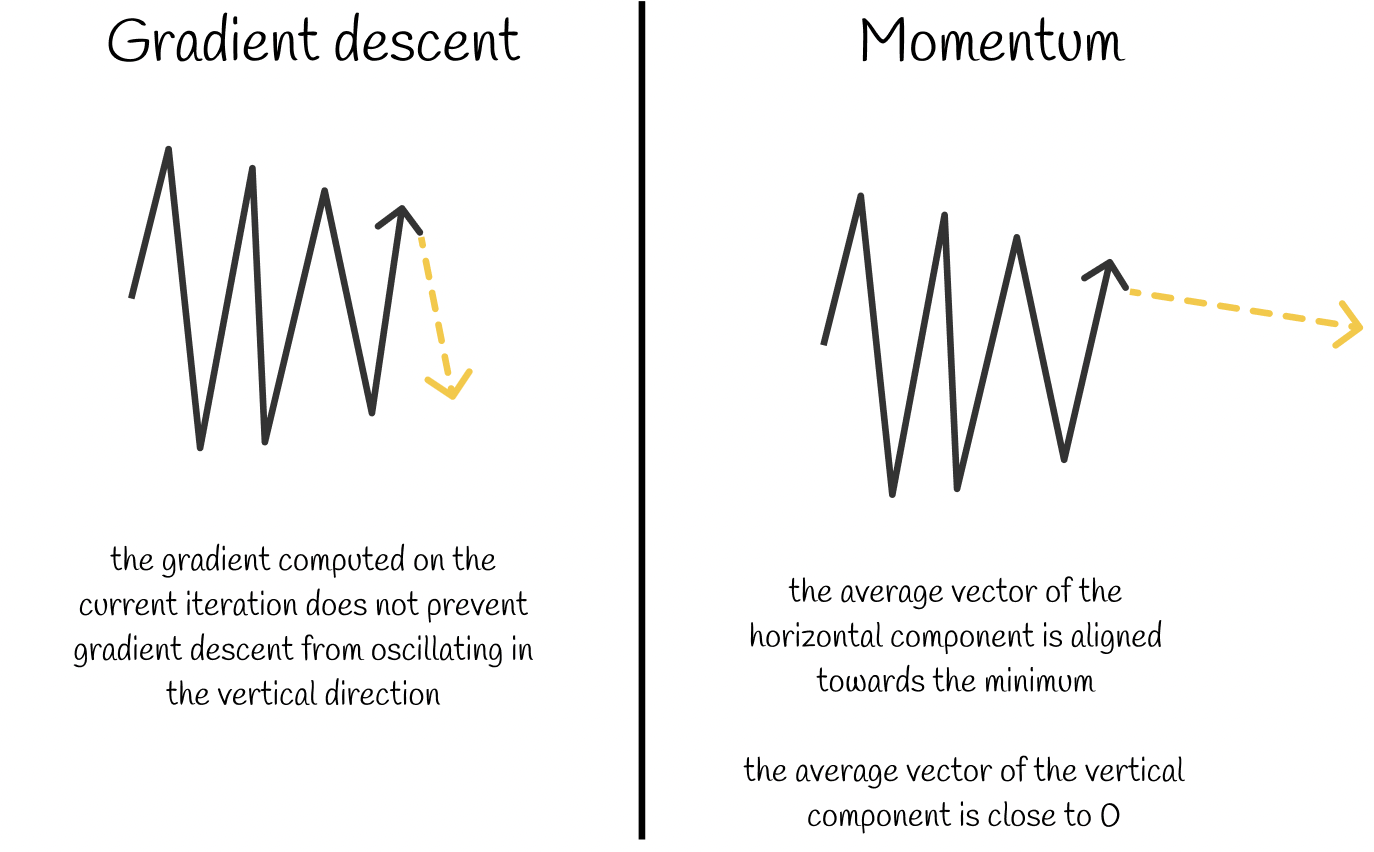
為了解決 SGD 的震盪問題並加速收斂，引入了動量 (Momentum) 的概念。它累積了過去梯度的指數加權平均，使得參數更新方向更平滑，並有助於衝過平坦區域或局部最小值。
#32
★★★
自適應學習率優化器 (Adaptive Learning Rate Optimizers)
改進方法
這類優化器（如 Adagrad, RMSprop, Adam）能夠為每個參數自動調整學習率。通常，對於更新頻繁的參數使用較小的學習率，對於更新不頻繁的參數使用較大的學習率。
Adam (Adaptive Moment Estimation) 是目前非常流行和常用的自適應優化器，結合了動量和 RMSprop 的思想。
#33
★★★★
學習率 (Learning Rate) 的重要性與調整
核心超參數
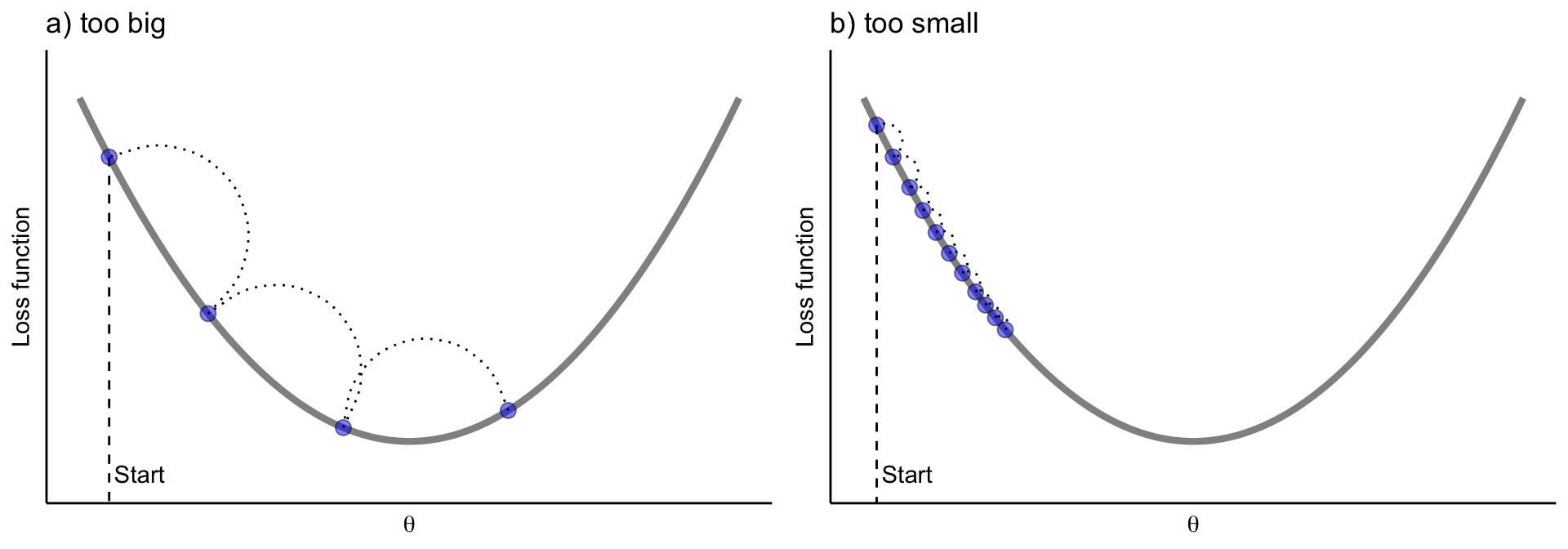
學習率 是最重要的超參數之一，它控制了參數更新的步長。
  • 學習率過大：可能導致優化過程在最小值附近震盪甚至發散，無法收斂。
  • 學習率過小：可能導致收斂速度過慢，或者陷入局部最小值。
通常需要仔細調整，或使用學習率衰減 (Learning Rate Decay/Scheduling) 策略（例如，訓練過程中逐漸降低學習率）。
#34
★★★★★
模型評估指標 (Model Evaluation Metrics) - 分類問題
常用指標
用於評估分類模型性能的常用指標：
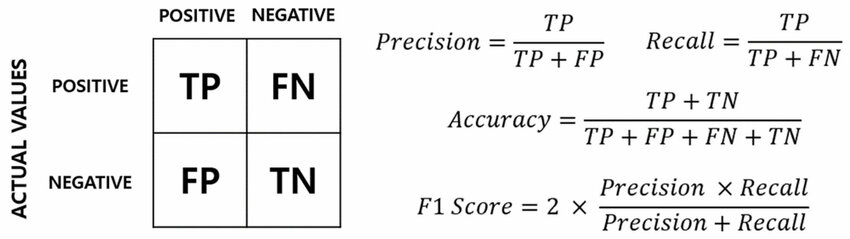
  • 準確率 (Accuracy): 整體預測正確的比例（在類別不平衡時可能具誤導性）。
  • 精確率 (Precision): 預測為正類的樣本中，實際為正類的比例。(= TP / (TP + FP))
  • 召回率 (Recall) / 敏感度 (Sensitivity) / 真陽性率 (TPR): 實際為正類的樣本中，被正確預測為正類的比例。(= TP / (TP + FN))
  • F1 分數 (F1 Score): 精確率和召回率的調和平均數，綜合考量兩者。
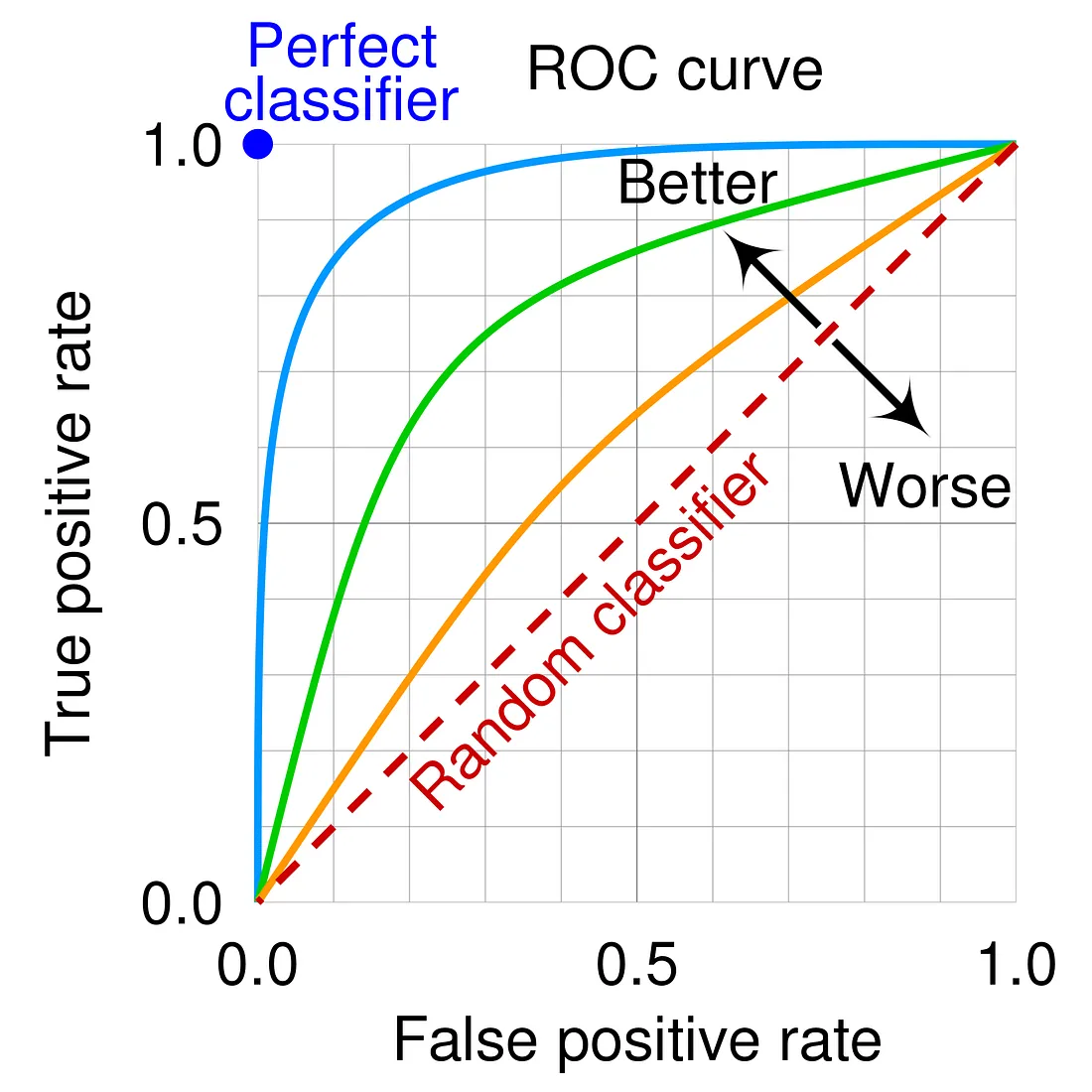
  • AUC (Area Under the ROC Curve): ROC 曲線下的面積，衡量模型區分正負類能力的整體指標。
  • 混淆矩陣 (Confusion Matrix): 展示 TP, FP, TN, FN 的表格。
(參考 L23303, 樣題 Q7, Q14)




#35
★★★★★
模型評估指標 (Model Evaluation Metrics) - 迴歸問題
常用指標
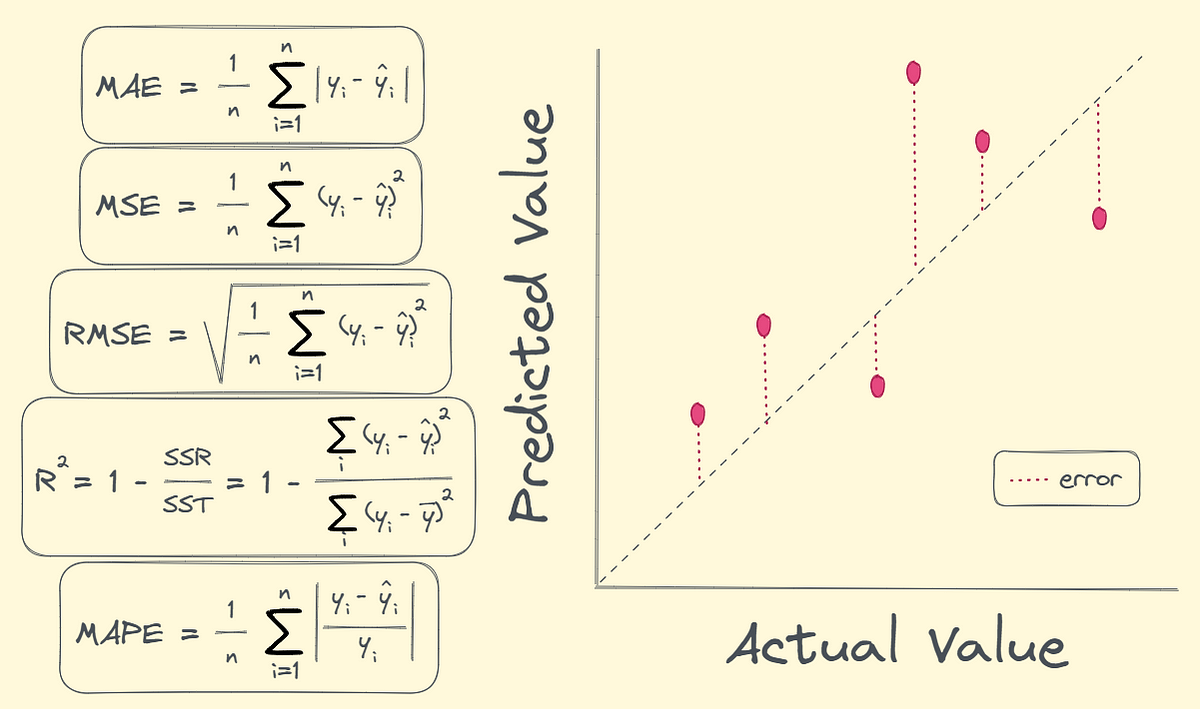
用於評估迴歸模型性能的常用指標：
  • 平均絕對誤差 (MAE, Mean Absolute Error): 預測值與真實值之間絕對誤差的平均值。
  • 均方誤差 (MSE, Mean Squared Error): 預測值與真實值之間誤差平方的平均值。
  • 均方根誤差 (RMSE, Root Mean Squared Error): MSE 的平方根，量綱與目標變數相同。
  • 決定係數 (R-squared, R²): 解釋了模型能夠解釋目標變數變異性的比例，值越接近 1 越好。(參考樣題 Q14)
  • 調整後 R² (Adjusted R-squared): 考慮了特徵數量的 R²，用於比較不同特徵數的模型。
(參考 L23303, 樣題 Q14)
#36
★★★★
根據業務目標選擇評估指標
選擇考量
沒有單一的最佳評估指標。選擇哪個（或哪些）指標來優化模型，應該基於具體的業務問題和目標。例如：
  • 在疾病檢測中，可能更關心召回率（ minimising 假陰性，避免漏診）。
  • 在垃圾郵件過濾中，可能更關心精確率（ minimising 假陽性，避免誤判正常郵件）。
  • 在預測房價中，RMSE 或 MAE 可能是主要指標。
需要理解不同指標的側重點。
#37
★★★★
訓練集、驗證集、測試集 的劃分與用途
數據劃分
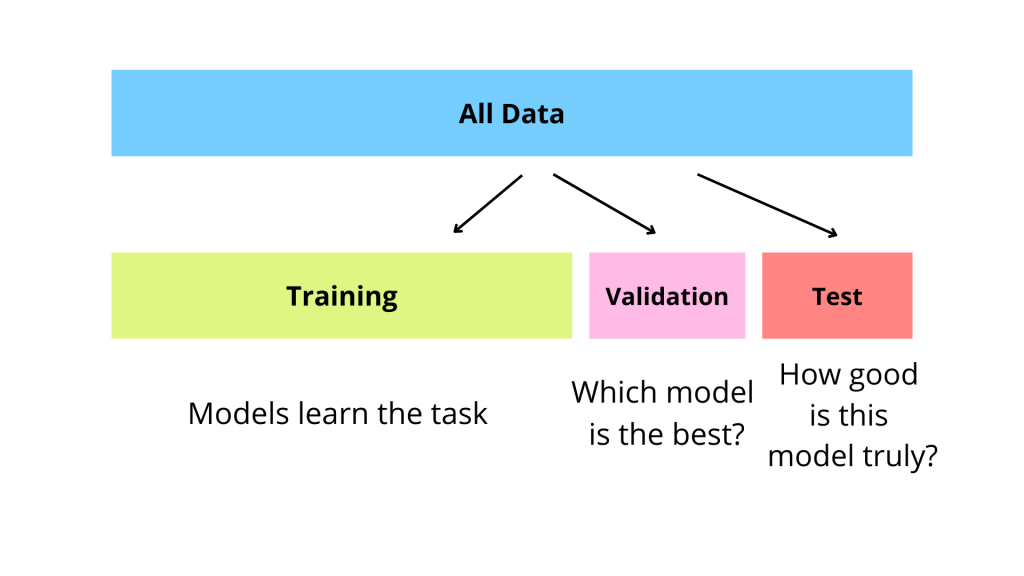
為了可靠地評估和調整模型，通常將數據劃分為：
  • 訓練集 (Training Set): 用於訓練模型，讓模型學習數據中的模式。
  • 驗證集 (Validation Set): 用於調整模型的超參數和進行模型選擇。模型在訓練過程中會根據驗證集的性能進行調整（例如，提早停止）。
  • 測試集 (Test Set): 獨立的數據集，僅在模型訓練和超參數調整完成後使用，用於最終評估模型的泛化能力。測試集不應參與任何訓練或調整過程。
(在交叉驗證中，原始訓練集會被進一步劃分為訓練摺和驗證摺)
#38
★★★★
偏誤-變異數權衡 (Bias-Variance Trade-off)
核心概念
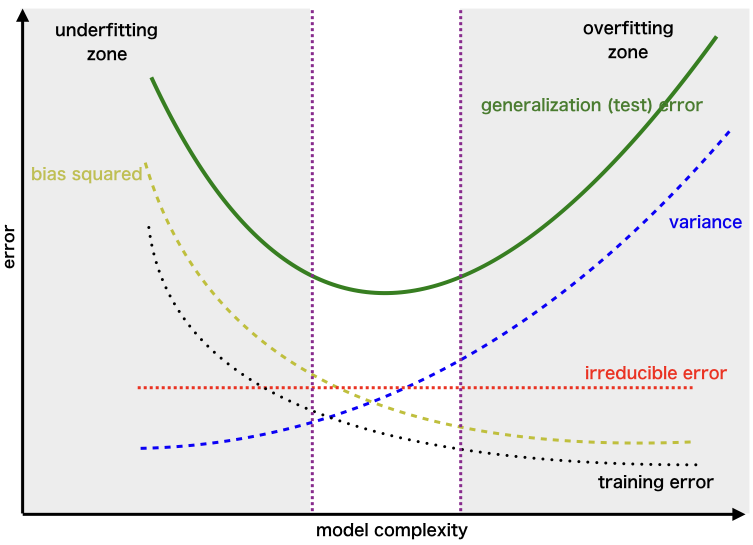
模型預測誤差通常可以分解為偏誤 (Bias)、變異數 (Variance) 和不可避免的噪聲。
  • 偏誤：模型假設與真實模式之間的差異（高偏誤導致欠擬合）。
  • 變異數：模型對訓練數據變化的敏感度（高變異數導致過擬合）。
通常，降低偏誤會增加變異數，反之亦然。模型調整的目標是在兩者之間找到一個平衡點，以最小化總體預期誤差。增加模型複雜度通常會降低偏誤但增加變異數；正則化通常會增加偏誤但降低變異數。
#39
★★★★
超參數調整的計算成本考量
實務考量
超參數調整（特別是網格搜尋和結合交叉驗證時）可能需要訓練和評估大量模型，計算成本非常高昂，尤其對於複雜模型和大規模數據集。在實務中，需要在調整的徹底性和可用的計算資源/時間之間進行權衡。隨機搜尋和貝氏優化等方法旨在提高效率。
#40
★★★
自動化機器學習 (AutoML) 與超參數優化
相關技術
AutoML 旨在自動化機器學習流程的各個環節，包括模型選擇和超參數優化 (HPO)。許多 AutoML 工具內部使用了先進的超參數調整策略（如貝氏優化、演化演算法）。雖然 AutoML 可以簡化流程，但理解背後的調整原理仍然重要。(參考樣題 Q5 提到 AutoML 的趨勢)
#41
★★★★
常用的超參數調整工具/函式庫
工具舉例
許多機器學習函式庫提供了內建或可整合的超參數調整工具：
  • Scikit-learn (Python): 提供 GridSearchCV 和 RandomizedSearchCV。
  • Hyperopt (Python): 實現了貝氏優化等策略。
  • Optuna (Python): 一個專注於超參數優化的框架，支持多種策略。
  • Keras Tuner (Python): 用於 Keras/TensorFlow 模型的超參數調整。
  • 雲端平台工具：如 Google Cloud AI Platform Vizier, AWS SageMaker Automatic Model Tuning, Azure Machine Learning Hyperparameter Tuning。
#42
★★★
實驗追蹤與管理 (Experiment Tracking)
實務考量
在進行超參數調整時，會運行大量實驗。使用實驗追蹤工具（如 MLflow, Weights & Biases, TensorBoard）來記錄每次實驗的超參數、代碼版本、數據集、評估指標和生成的模型非常重要。這有助於結果的可重現性、比較和管理。
#43
★★★
數據量對過擬合/欠擬合的影響
影響關係
  • 數據量過少：模型更容易過擬合，因為它可以輕易記住少量數據的細節。
  • 數據量增加：通常有助於減輕過擬合，因為模型需要學習更具泛化性的模式才能適應更多樣的數據。對於欠擬合的模型，增加數據量可能幫助不大，關鍵在於模型本身太簡單。
#44
★★★
超參數空間的定義
定義要素
在進行超參數調整前，需要定義每個待調整超參數的搜尋範圍或分佈。這包括確定超參數的類型（連續、離散）、範圍（最小值、最大值）以及可能的取值方式（線性、對數）。合理的超參數空間定義對調整效率和結果至關重要。
#45
★★
數據增強 (Data Augmentation) 作為正則化
概念
數據增強（例如，對圖像進行旋轉、裁剪、變色）可以人工增加訓練數據的多樣性，強迫模型學習更穩健、對變換不變的特徵。從效果上看，它類似於一種正則化，有助於提高模型的泛化能力和防止過擬合。
#46
★★
嵌套交叉驗證 (Nested Cross-Validation)
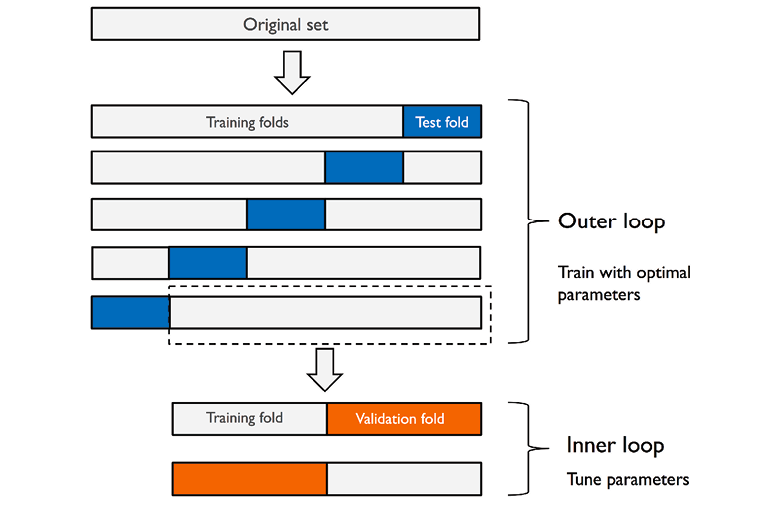
進階方法
當同時需要進行超參數調整和模型性能評估時，為避免資訊洩漏導致過於樂觀的評估結果，可以使用嵌套交叉驗證。它包含外層循環（用於評估最終模型性能）和內層循環（用於在每次外層循環的訓練集上進行超參數調整）。計算成本更高。
#47
★★★
模型選擇 (Model Selection)
概念
在嘗試了不同的模型架構、演算法或超參數組合後，需要根據驗證集或交叉驗證的評估結果，選擇最終部署的模型。選擇的標準應基於預先定義的、與業務目標一致的評估指標。模型調整是模型選擇過程中的重要環節。(參考 L23302)
#48
★★
統計顯著性檢定 (Statistical Significance Testing)
評估輔助
在比較不同模型或不同超參數組合的性能時，除了比較平均指標外，可以使用統計檢定（如 t-檢定、配對 t-檢定）來判斷觀察到的性能差異是否具有統計學上的顯著性，而不僅僅是隨機波動。
#49
★★
超參數與模型可解釋性的關係
影響關係
某些超參數的選擇會影響模型的可解釋性 (Interpretability)。例如，較淺的決策樹比深度複雜的隨機森林更容易解釋；L1 正則化產生的稀疏模型也可能有助於理解哪些特徵最重要。在調整時，除了性能，也可能需要考慮可解釋性的需求。
#50
★★
模型重新訓練與持續優化
實務考量
模型部署後，由於數據分佈可能隨時間變化（數據漂移, Data Drift / 概念漂移, Concept Drift），模型的性能可能會下降。因此需要定期監控模型性能，並根據需要使用新數據重新訓練模型，甚至重新進行超參數調整，以維持或提升模型效果。
#51
★★
模型複雜度 (Model Complexity)
概念
指模型擬合數據的能力。複雜度過高易導致過擬合，複雜度過低易導致欠擬合。模型調整常涉及控制或選擇適當的模型複雜度。
#52
★
超參數的敏感性分析
分析方法
評估模型性能對特定超參數變化的敏感程度。有助於識別哪些超參數對模型影響最大，需要更仔細地調整。
#53
★
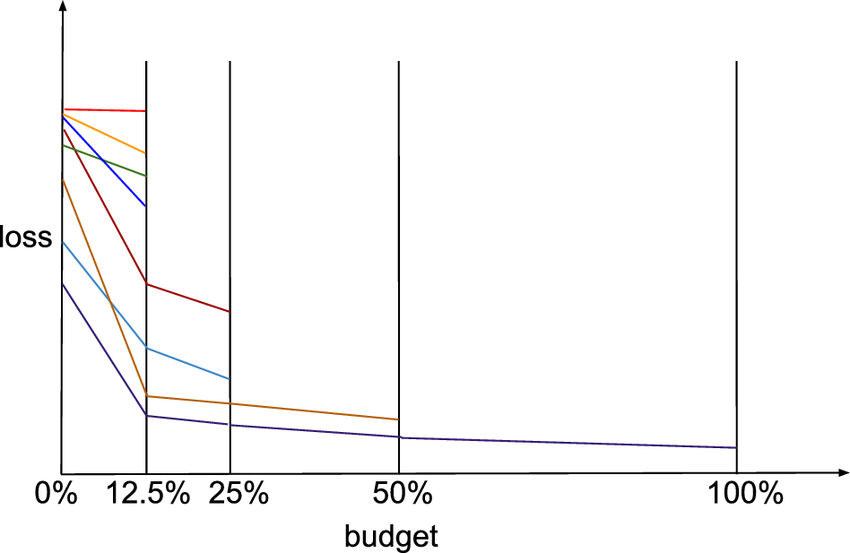
連續減半 (Successive Halving)
調整策略
一種資源分配策略，用於加速超參數搜索。它將固定資源分配給大量候選配置，並在早期階段淘汰表現不佳的配置，將更多資源集中在有希望的配置上。
#54
★
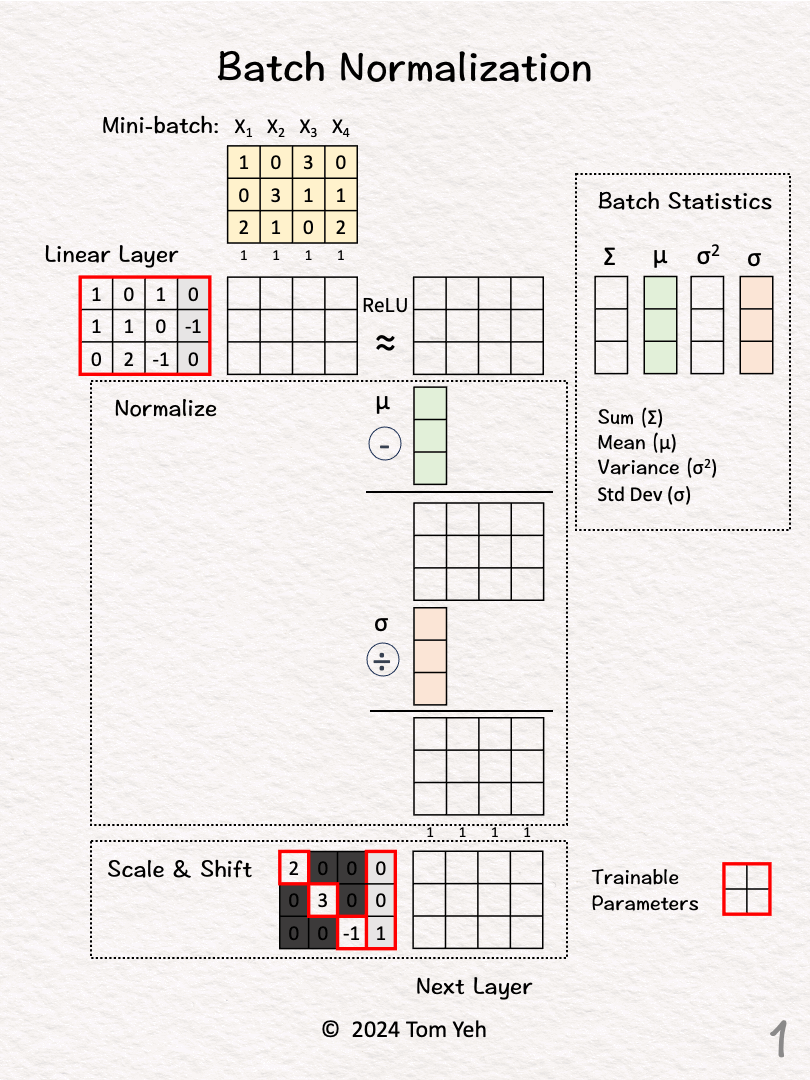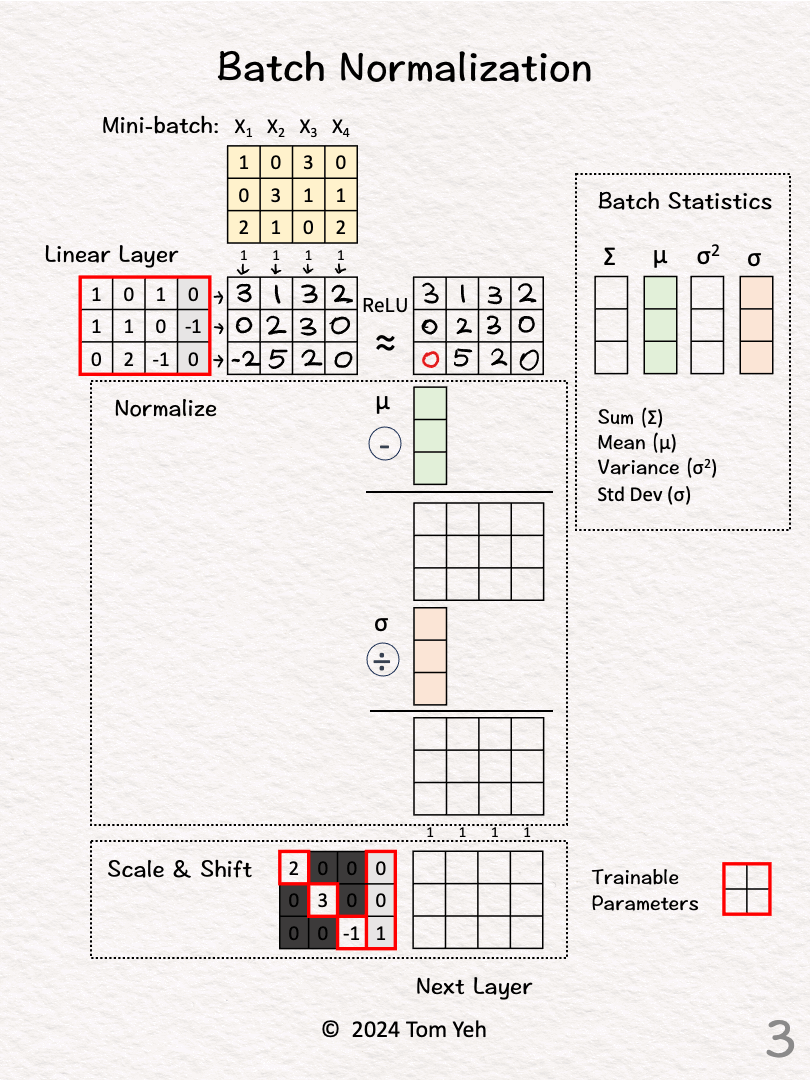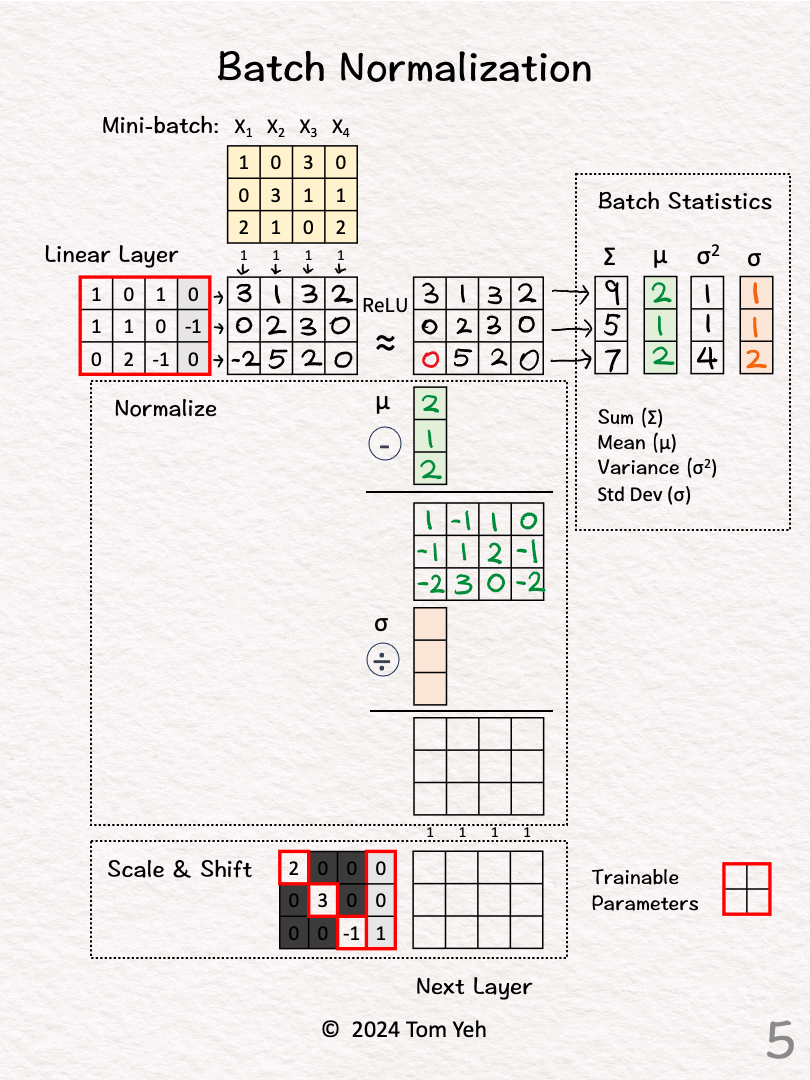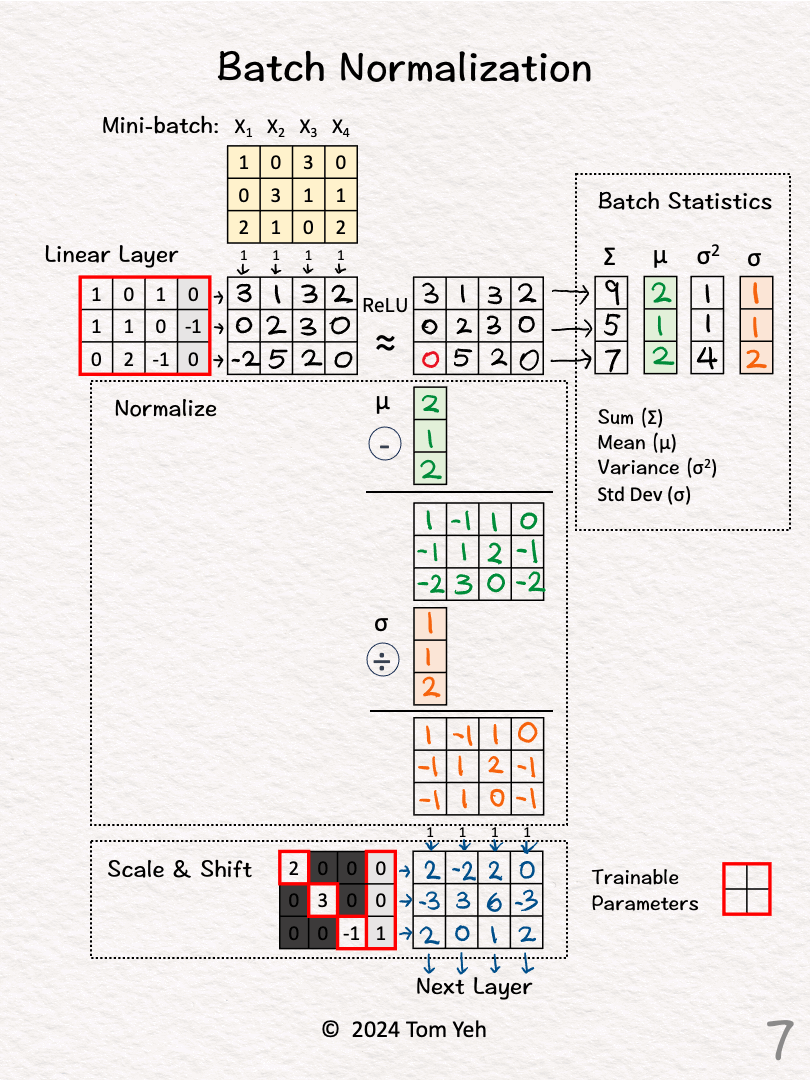
批次正規化 (Batch Normalization)
技術說明 (神經網路)
對神經網路每一層的輸入進行標準化處理。有助於穩定訓練過程，加速收斂，並具有一定的正則化效果。
#55
★
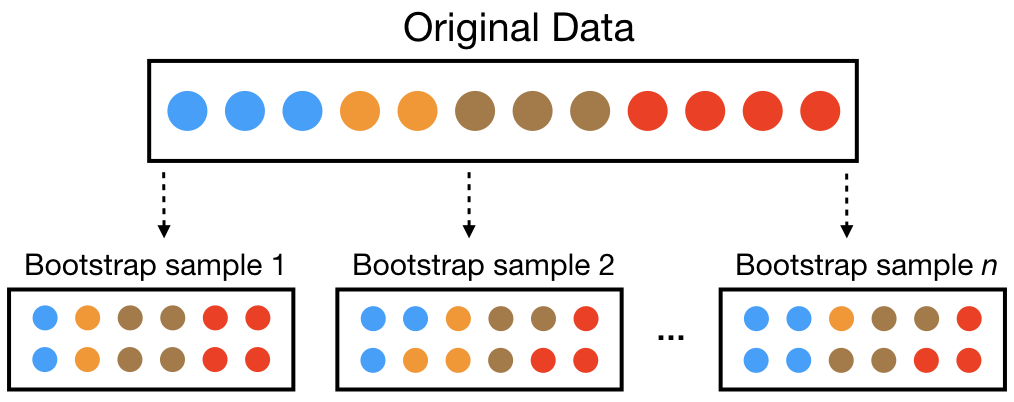
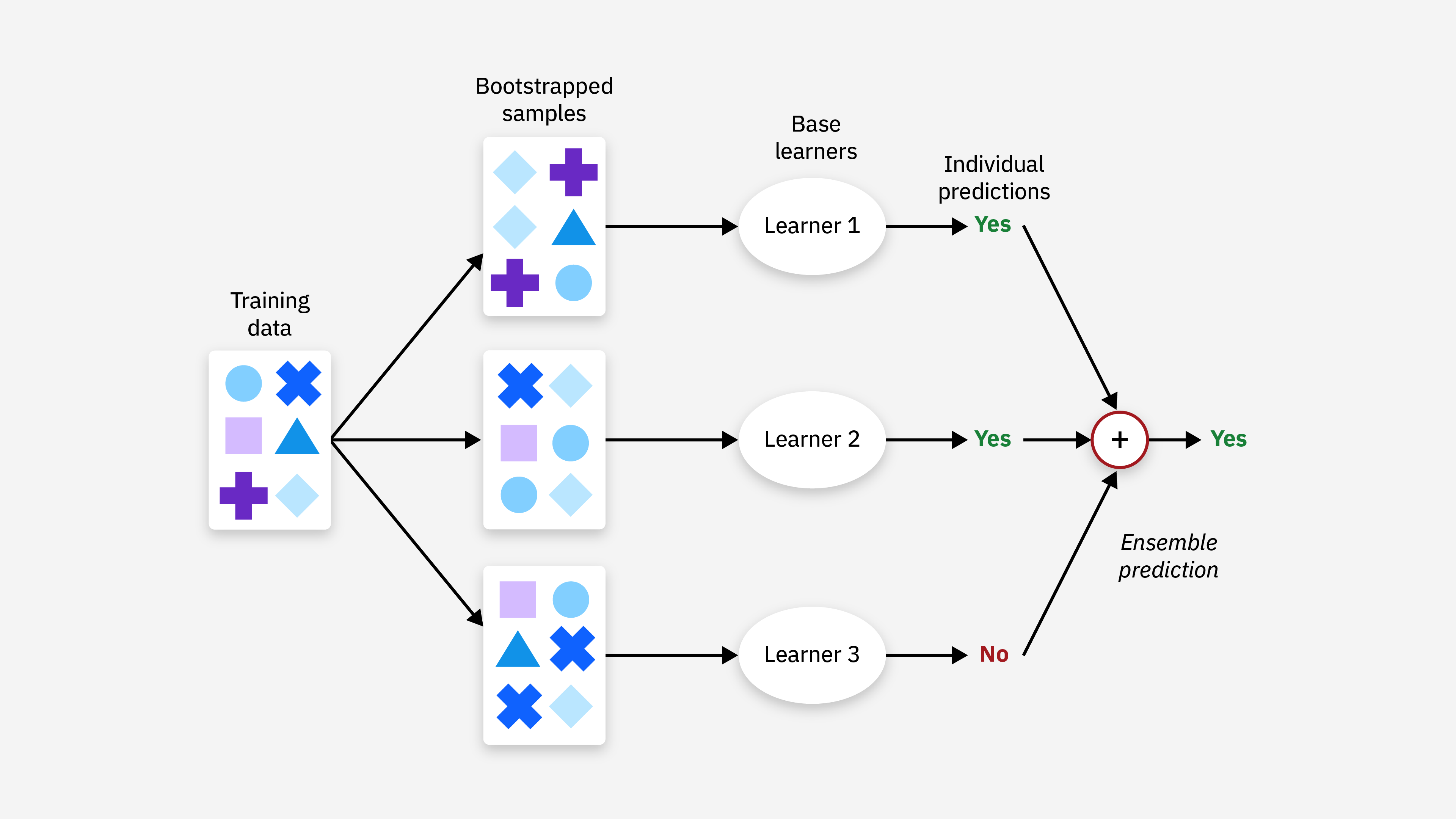
自助法 (Bootstrap) 抽樣
抽樣技術
一種有放回的抽樣方法，可用於估計統計量的變異數或建立信賴區間。在機器學習中，可用於評估模型穩定性或作為集成方法（如 Bagging）的基礎。與交叉驗證目的相似但方法不同。
#56
★
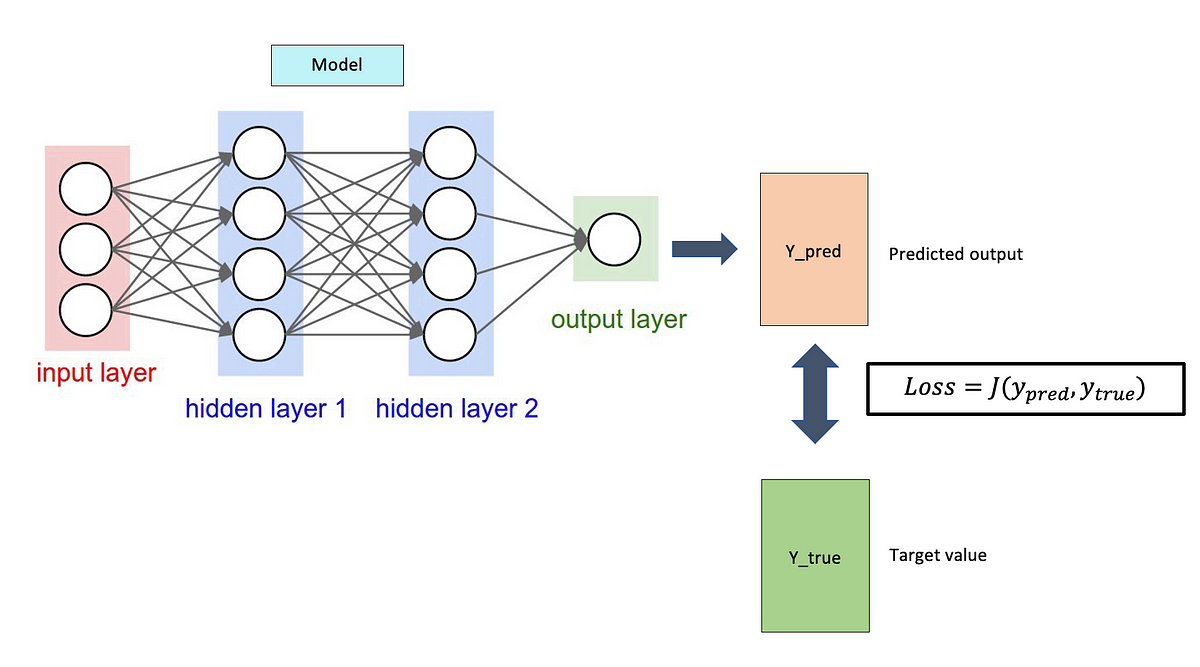
損失函數 (Loss Function) 的選擇
概念
損失函數衡量模型預測與真實值之間的差異。優化演算法的目標是最小化損失函數。選擇合適的損失函數（如用於分類的交叉熵損失，用於迴歸的 MSE）對模型訓練至關重要，有時也需要根據特定目標進行調整。
#57
★
集成方法 (Ensemble Methods)
概念
結合多個模型的預測以獲得比單一模型更好性能的方法（如 Bagging, Boosting, Stacking）。雖然本身是建模技術，但集成方法通常能提高模型的穩定性和泛化能力，減少過擬合風險，可視為一種廣義的優化策略。
#58
★
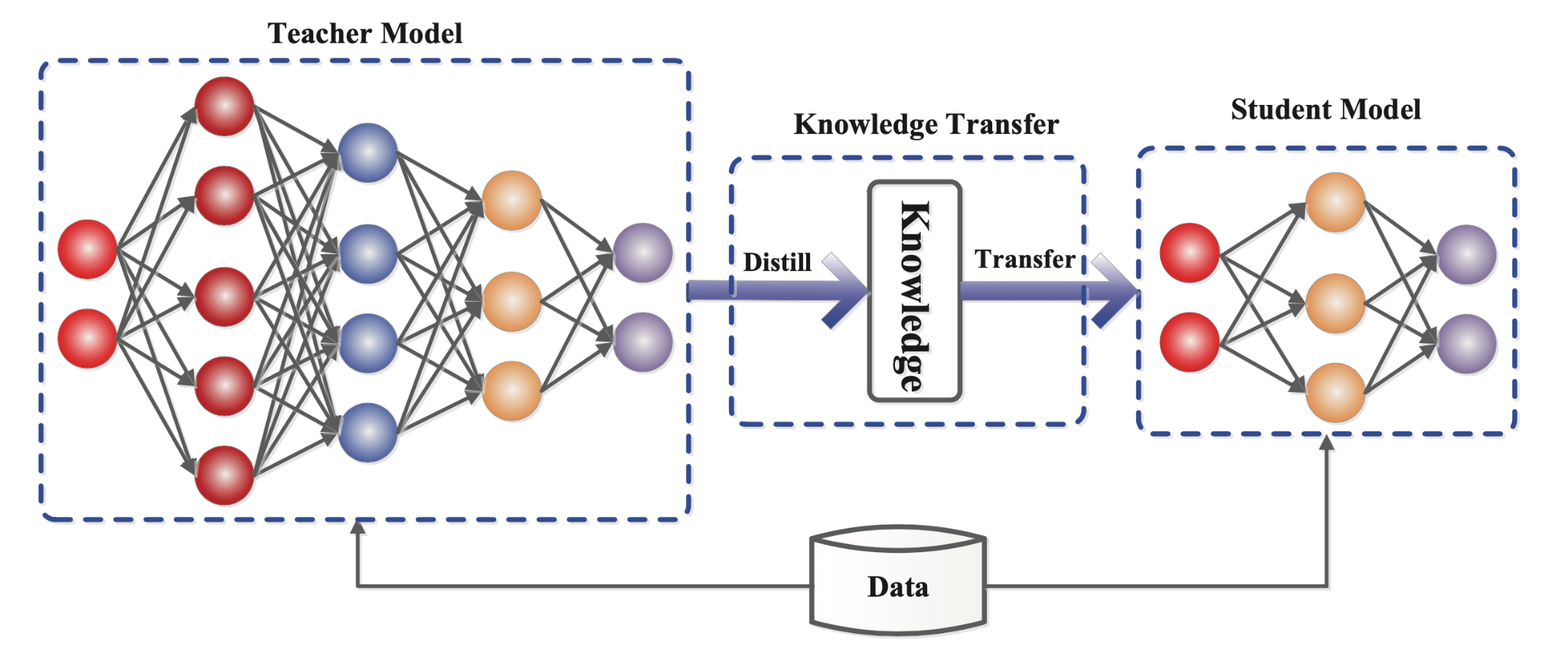
模型壓縮 (Model Compression)
優化目標
旨在減小模型的大小和降低推論時的計算成本，同時盡量保持模型性能。方法包括權重剪枝 (Pruning)、量化 (Quantization)、知識蒸餾 (Knowledge Distillation) 等。是模型部署前的常見優化步驟。
#59
★
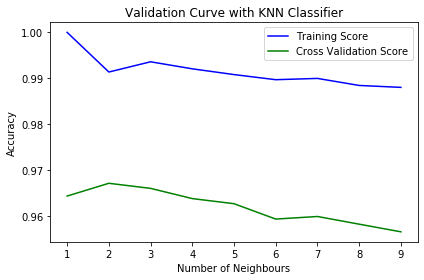
驗證曲線 (Validation Curves)
診斷工具
繪製模型性能隨單個超參數變化（例如正則化強度、樹的深度）的曲線，同時顯示訓練集和驗證集的性能。有助於理解特定超參數對過擬合/欠擬合的影響，並選擇合適的取值範圍。
#60
★
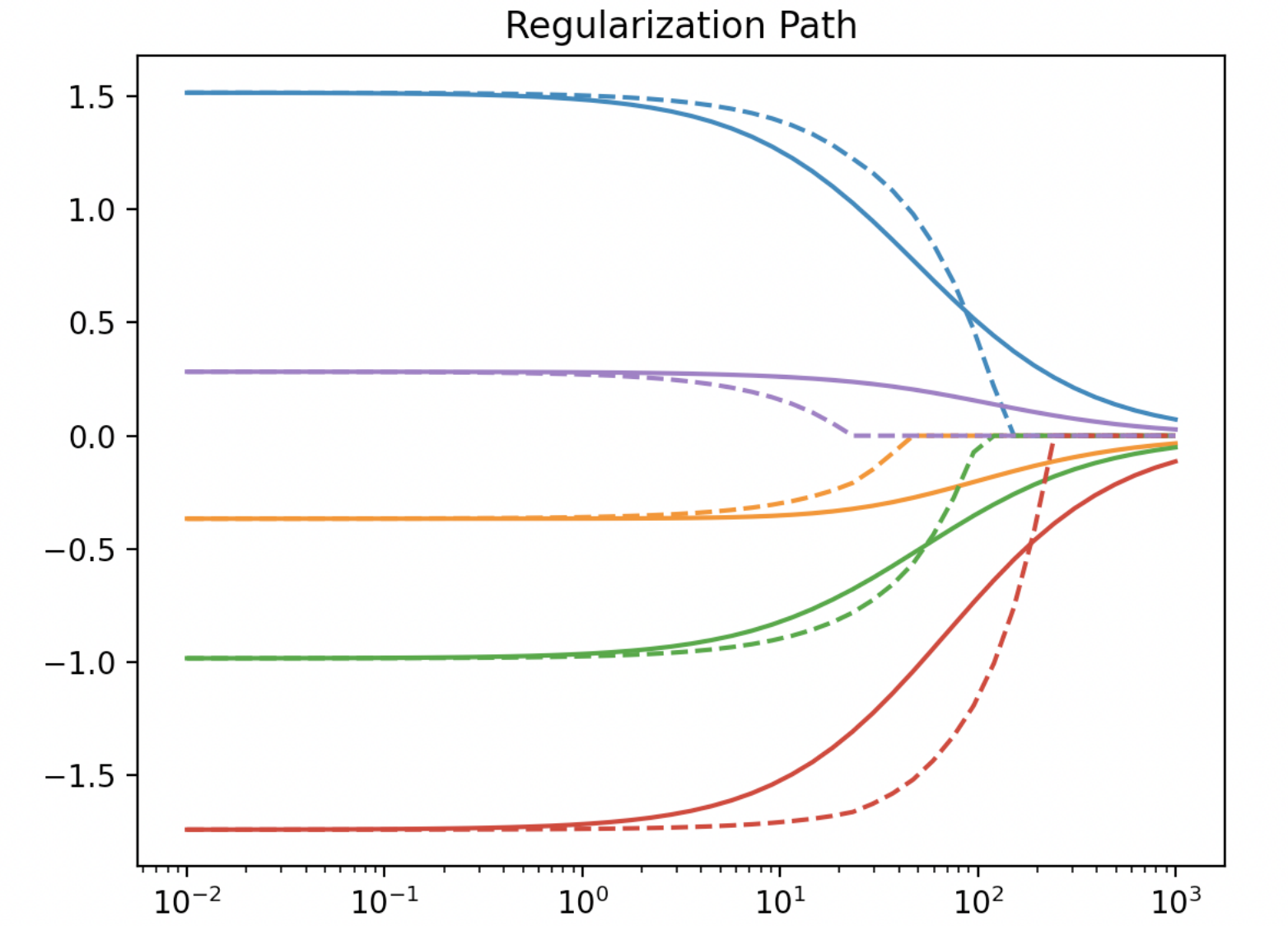
正則化路徑 (Regularization Path)
概念
繪製模型參數（係數）隨正則化強度超參數（如 L1 的 alpha）變化的軌跡。有助於理解不同特徵在不同正則化強度下的重要性變化，特別是用於 Lasso 的特徵選擇過程。
沒有找到符合條件的重點。
↑