iPAS AI應用規劃師 考試重點

L23303 模型訓練、評估與驗證
主題分類
1
數據集劃分 (Train/Val/Test)
2
模型訓練基礎
3
分類模型評估指標
4
迴歸模型評估指標
5
模型驗證技術
6
過擬合與欠擬合診斷
7
評估指標選擇考量
8
模型比較與選擇
#1
★★★★★
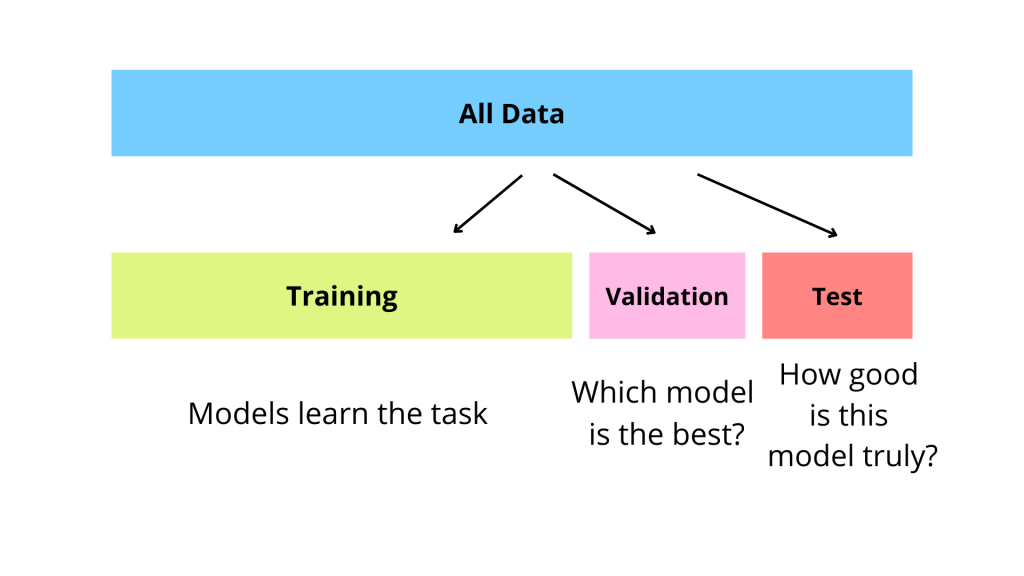
訓練集 (Training Set) - 用途
核心概念
訓練集 是用於訓練機器學習模型的數據子集。模型透過分析訓練集中的數據來學習模式、規律和關係，並調整其內部參數（權重和偏置）。訓練集的品質和代表性直接影響模型的學習效果。
#2
★★★★★
驗證集 (Validation Set) - 用途
核心概念
驗證集 是用於在模型訓練過程中評估不同超參數組合或模型架構性能的數據子集。它不直接參與模型參數的學習，而是用來指導超參數調整（例如，選擇最佳學習率）和模型選擇（例如，比較不同演算法）。驗證集有助於監控和防止過擬合。
#3
★★★★★
測試集 (Test Set) - 用途
核心概念
測試集 是一份獨立的、從未在訓練或驗證階段使用過的數據子集。它用於在模型訓練和調整完成後，對最終選定的模型進行一次性的、無偏的性能評估，以估計模型在真實世界未見數據上的泛化能力 (Generalization Ability)。測試集的性能是衡量模型最終效果的關鍵指標。
#4
★★★★
數據集劃分的重要性與原則
重要原則
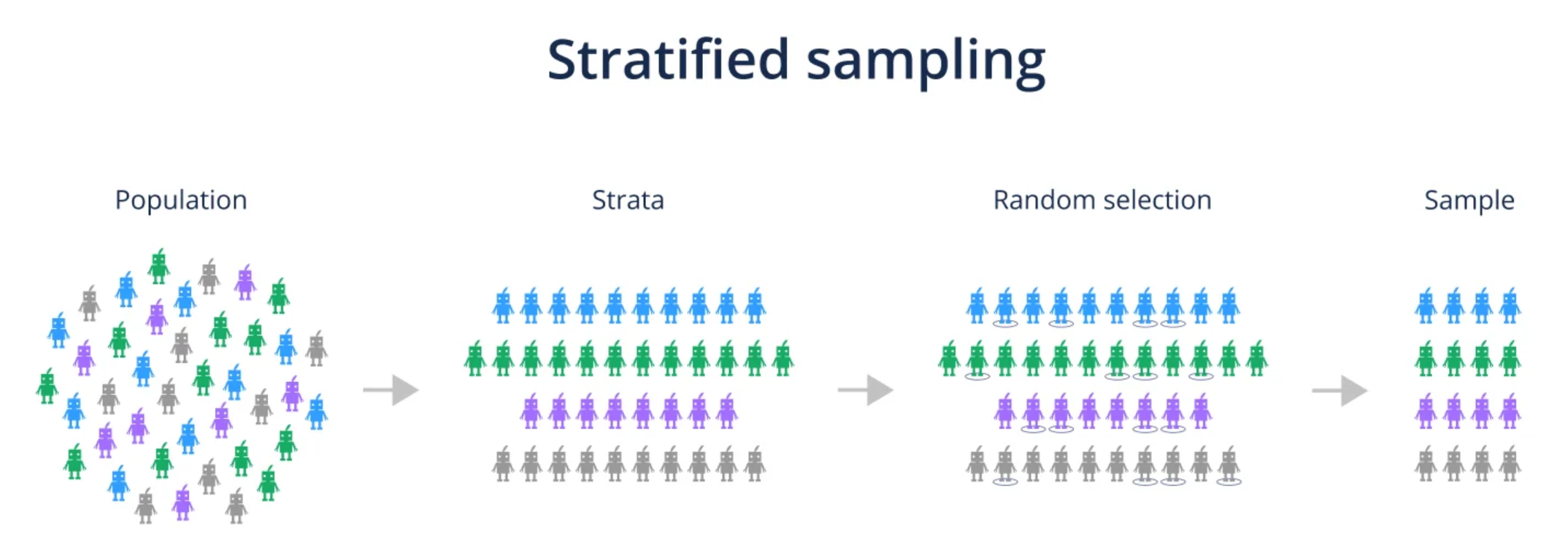
  • 獨立性：驗證集和測試集應與訓練集獨立，以提供對模型泛化能力的無偏估計。測試集尤其重要，絕不能用於訓練或調優。
  • 代表性：三個子集都應能代表原始數據的分佈特性。對於分類問題，常使用分層抽樣 (Stratified Sampling) 來確保各類別比例一致。
  • 劃分比例：沒有固定比例，常見的劃分方式如 60/20/20、70/15/15 或 80/10/10 (訓練/驗證/測試)。數據量大時，驗證集和測試集比例可稍小。
#5
★★★★
模型訓練流程概述
基本步驟
模型訓練通常涉及以下步驟：
  1. 選擇模型架構與演算法。
  2. 定義損失函數 (Loss Function) 來衡量預測與真實值之間的差異。
  3. 選擇優化演算法 (Optimizer) (如 SGD, Adam) 來最小化損失函數。
  4. 設定超參數（如學習率、批次大小）。
  5. 使用訓練集數據，透過優化演算法迭代更新模型參數。
  6. 在訓練過程中或結束後，使用驗證集評估模型性能並進行調整。
#6
★★★★
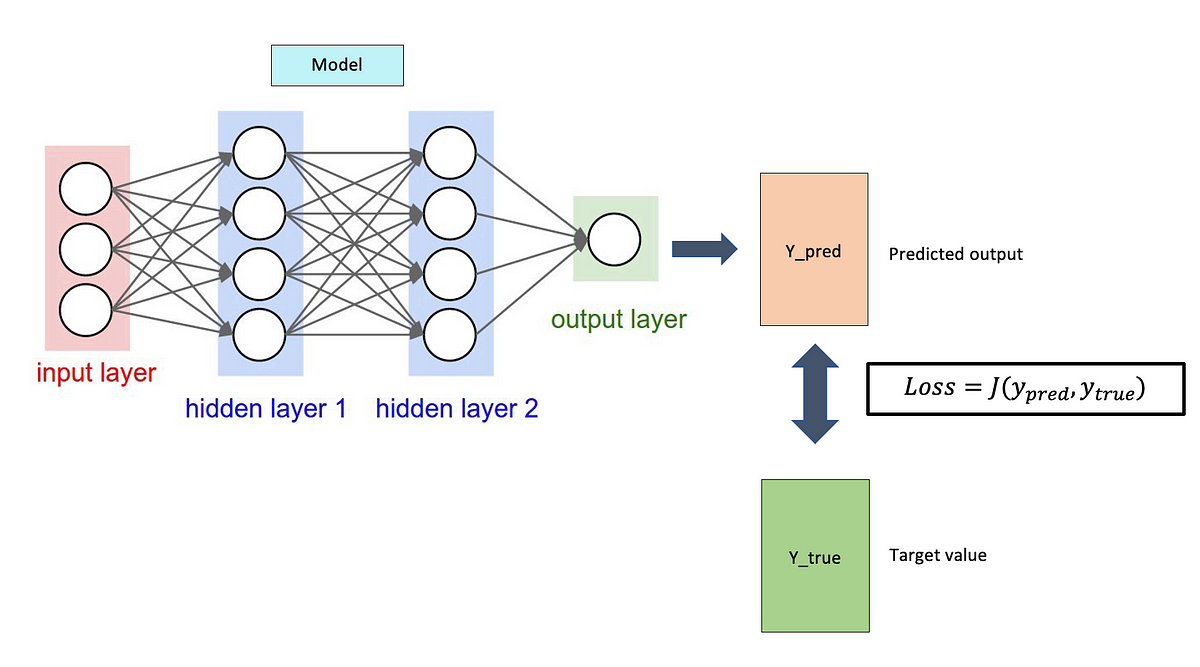
損失函數 (Loss Function) / 成本函數 (Cost Function)
核心概念
損失函數 用於量化單個樣本的預測錯誤程度，而成本函數通常指整個訓練集上損失函數的平均值。模型訓練的目標是找到一組模型參數，使得成本函數最小化。損失函數的選擇取決於問題類型（分類、迴歸）。
#7
★★★
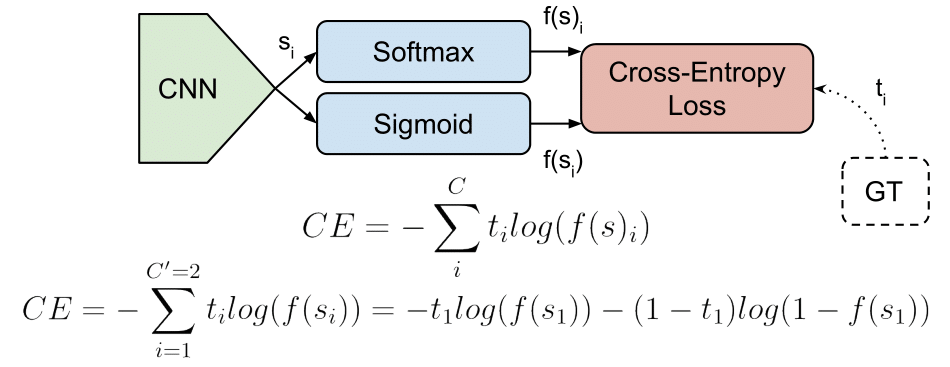
常見的損失函數 - 分類
舉例說明
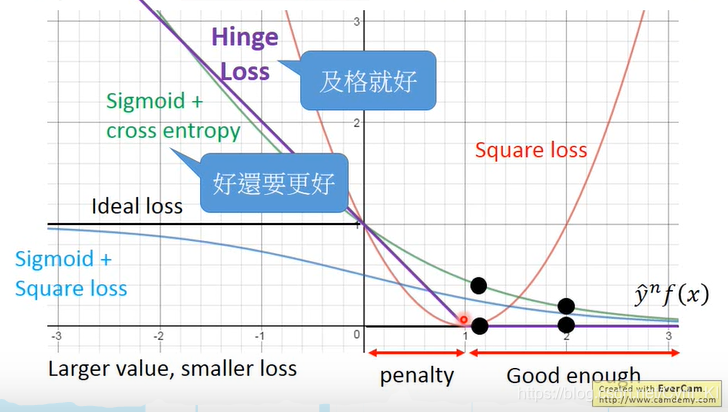
  • 交叉熵損失 (Cross-Entropy Loss): 最常用於分類問題，特別是輸出為機率時 (配合 Softmax 或 Sigmoid)。
  • Hinge損失 (Hinge Loss): 主要用於支持向量機 (SVM)。
#8
★★★
常見的損失函數 - 迴歸
舉例說明
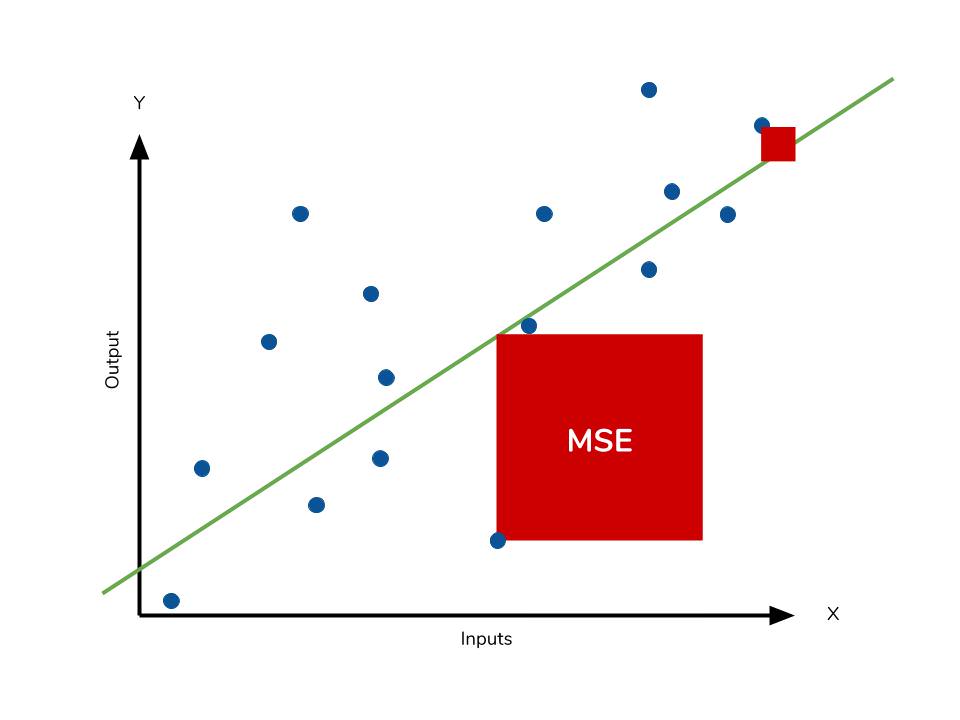
  • 均方誤差 (MSE, Mean Squared Error): 最常用的迴歸損失函數，計算預測值與真實值之差的平方的平均值。
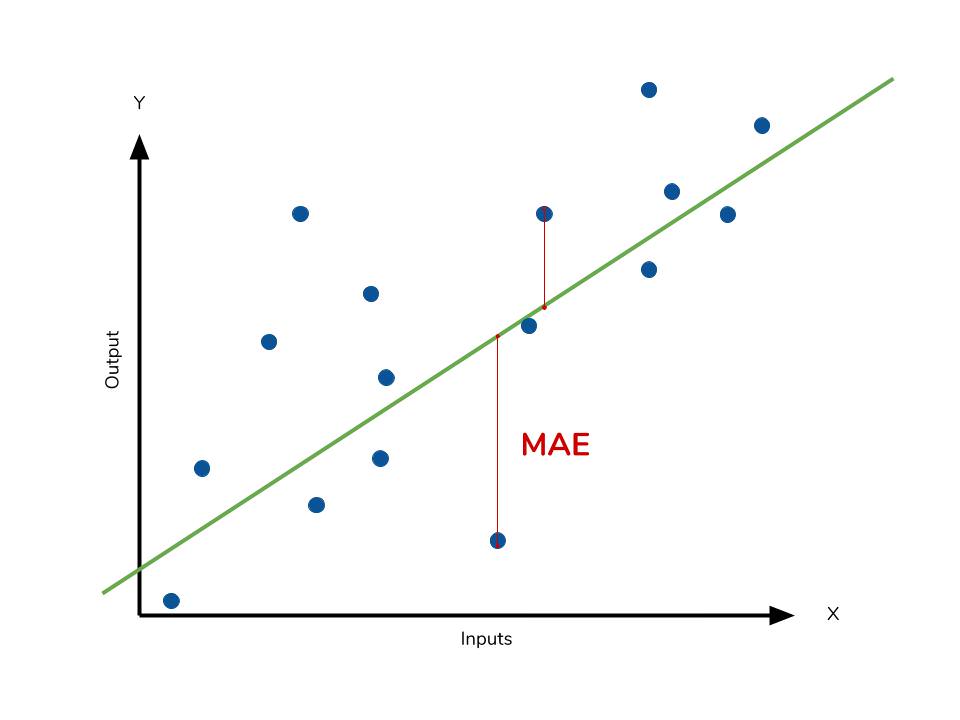
  • 平均絕對誤差 (MAE, Mean Absolute Error): 計算預測值與真實值之差的絕對值的平均值，對離群值較不敏感。
#9
★★★★
優化演算法 (Optimization Algorithms) 的作用
核心作用
優化演算法 (如 梯度下降法 及其變體) 負責根據損失函數計算出的梯度訊息，迭代地更新模型的參數，以逐步降低損失函數的值，使模型越來越接近最優解。
#10
★★★
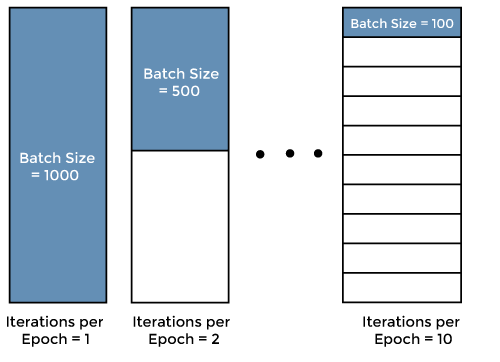
批次大小 (Batch Size) 與 訓練輪數 (Epochs)
訓練超參數
  • 批次大小：在小批量梯度下降中，每次參數更新所使用的樣本數量。影響梯度估計的穩定性和計算效率。
  • 訓練輪數：整個訓練集數據被模型完整地學習一遍的次數。訓練輪數過少可能導致欠擬合，過多可能導致過擬合（常配合提早停止使用）。
#11
★★★★★
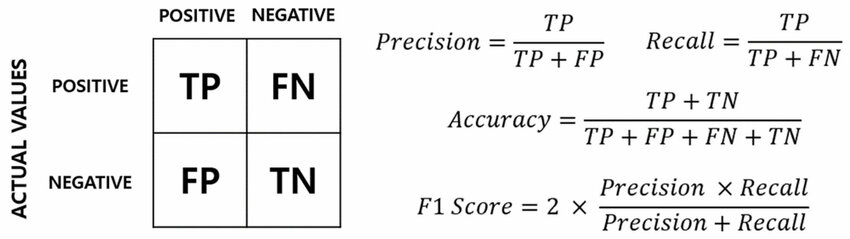
混淆矩陣 (Confusion Matrix)
核心工具 (分類)
混淆矩陣 是一個表格，用於視覺化分類模型的性能。它總結了模型預測結果與實際類別之間的關係，包含四個基本指標：
  • 真陽性 (TP, True Positive): 實際為正，預測也為正。
  • 假陽性 (FP, False Positive) / 型一錯誤 (Type I Error): 實際為負，預測為正。
  • 真陰性 (TN, True Negative): 實際為負，預測也為負。
  • 假陰性 (FN, False Negative) / 型二錯誤 (Type II Error): 實際為正，預測為負。
許多分類指標都基於混淆矩陣計算。
#12
★★★★★
準確率 (Accuracy)
評估指標 (分類)
準確率 是指模型預測正確的樣本數佔總樣本數的比例。
Accuracy = (TP + TN) / (Total Samples)
雖然直觀，但在類別不平衡 (Imbalanced Classes) 的情況下，準確率可能具有誤導性。例如，如果 99% 的樣本屬於負類，一個總是預測負類的模型準確率也能達到 99%。
#13
★★★★★
精確率 (Precision)
評估指標 (分類)
精確率 指的是在所有被模型預測為正類的樣本中，實際為正類的比例。
Precision = TP / (TP + FP)
高精確率意味著模型預測為正的樣本中很少有誤判（低假陽性率）。關注點是「預測為正的結果有多準確」。
#14
★★★★★
召回率 (Recall) / 敏感度 (Sensitivity) / 真陽性率 (TPR)
評估指標 (分類)
召回率 指的是在所有實際為正類的樣本中，被模型成功預測為正類的比例。
Recall = TP / (TP + FN)
高召回率意味著模型能夠找出大部分的正類樣本（低假陰性率）。關注點是「所有正樣本中，模型找出了多少」。
#15
★★★★★
F1 分數 (F1 Score)
評估指標 (分類, 參考樣題 Q14 選項)
F1 分數 是精確率和召回率的調和平均數 (Harmonic Mean)。
F1 = 2 * (Precision * Recall) / (Precision + Recall)
它試圖平衡精確率和召回率，當兩者都較高時，F1 分數也會較高。特別適用於類別不平衡或同時關注假陽性和假陰性的情況。
#16
★★★★
特異度 (Specificity) / 真陰性率 (TNR)
評估指標 (分類)
特異度 指的是在所有實際為負類的樣本中，被模型成功預測為負類的比例。
Specificity = TN / (TN + FP)
高特異度意味著模型能夠準確地識別出負類樣本（低假陽性率）。它與假陽性率 (FPR) 的關係是：Specificity = 1 - FPR。
#17
★★★★
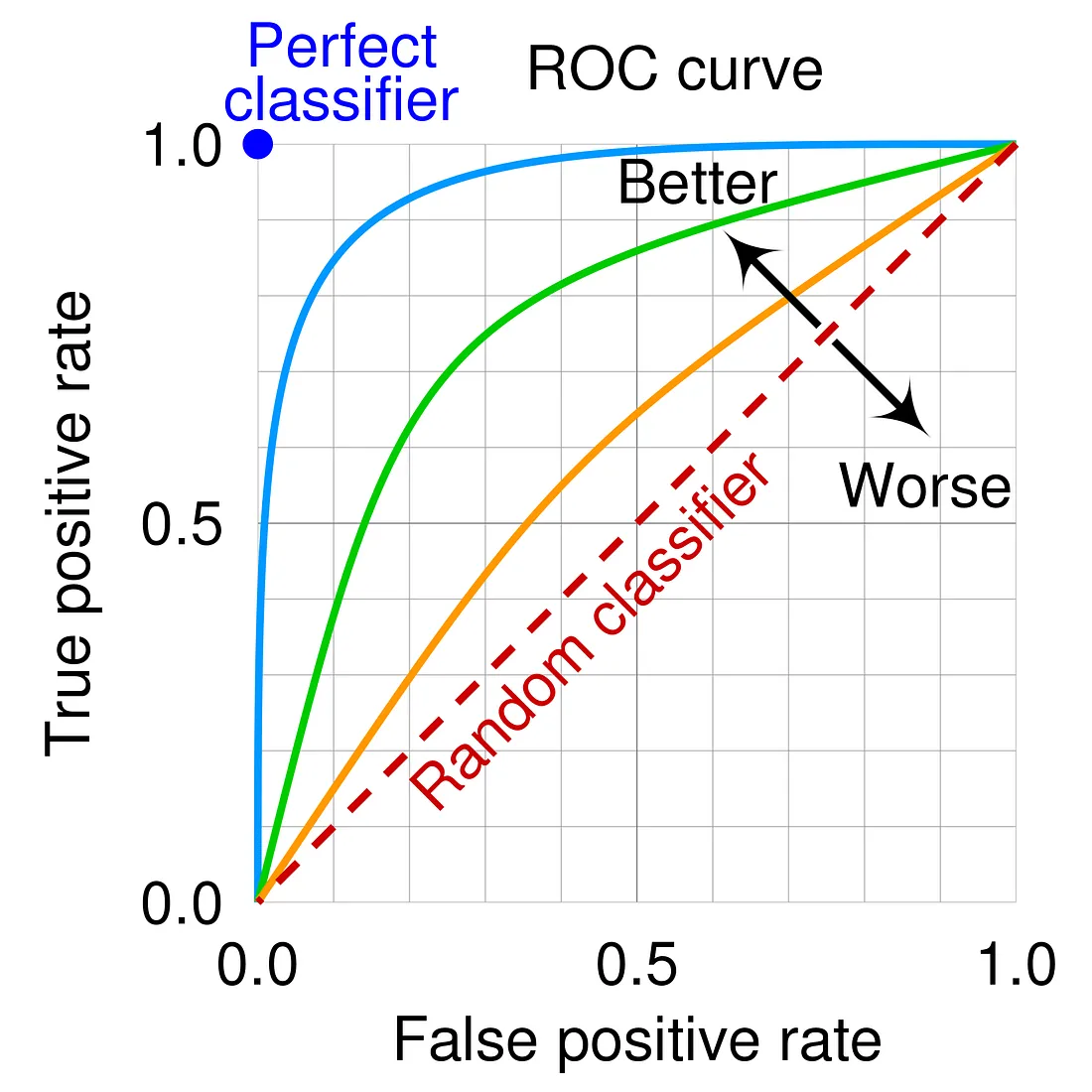
ROC 曲線 (Receiver Operating Characteristic Curve)
評估工具 (分類, 參考樣題 Q7)
ROC 曲線 是一個圖形化工具，用於展示分類模型在不同分類閾值下的性能。
  • 橫軸：假陽性率 (FPR = 1 - Specificity)
  • 縱軸：真陽性率 (TPR = Recall = Sensitivity)
曲線越靠近左上角（TPR 高，FPR 低），表示模型性能越好。它可以幫助比較不同模型的區分能力，並選擇合適的閾值。 樣題 Q7 指出 ROC 曲線繪製了 TPR 與 FPR 的關係。
#18
★★★★
AUC (Area Under the ROC Curve)
評估指標 (分類, 參考樣題 Q7, Q14 選項)
AUC 指的是 ROC 曲線下的面積。其值介於 0 到 1 之間。
  • AUC = 1：完美的分類器。
  • AUC = 0.5：模型沒有區分能力（相當於隨機猜測）。
  • AUC > 0.5：模型具有一定的區分能力，值越大越好。
AUC 是一個衡量模型整體區分正負類能力的指標，不受特定閾值選擇的影響，對類別不平衡問題也相對穩健。 樣題 Q7 提到 AUC 不一定等於 1。
#19
★★★
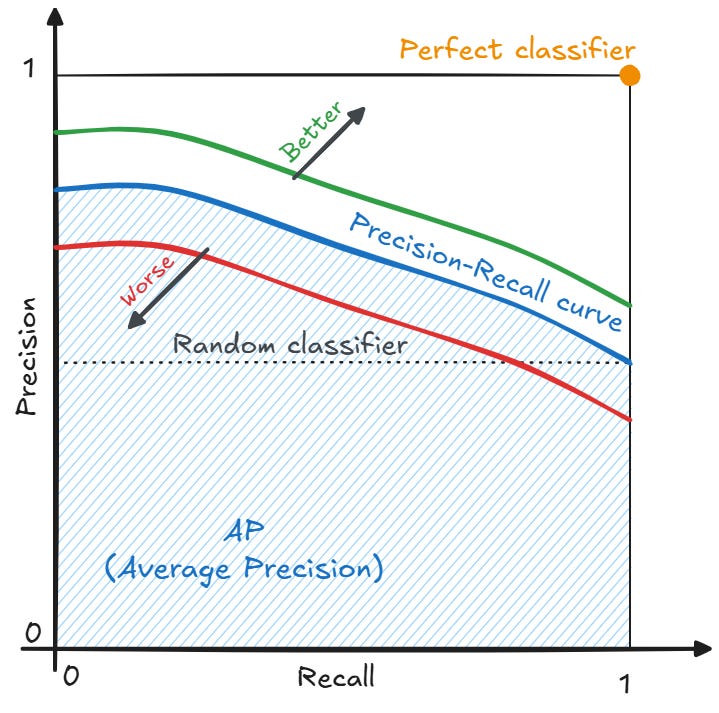
PR 曲線 (Precision-Recall Curve)
評估工具 (分類)
PR 曲線 繪製了在不同分類閾值下，精確率 (Precision) 與召回率 (Recall) 之間的關係。
  • 橫軸：召回率 (Recall)
  • 縱軸：精確率 (Precision)
曲線越靠近右上角（Precision 高，Recall 高），表示模型性能越好。在類別極度不平衡的情況下，PR 曲線通常比 ROC 曲線更能反映模型在少數類上的性能。
#20
★★★★★
均方誤差 (MSE, Mean Squared Error)
評估指標 (迴歸)
MSE 計算的是預測值與真實值之差的平方的平均值。
MSE = (1/n) * Σ(yᵢ - ŷᵢ)²
由於誤差被平方，MSE 對較大的誤差（離群值）非常敏感。值越小表示模型性能越好。
#21
★★★★
均方根誤差 (RMSE, Root Mean Squared Error)
評估指標 (迴歸)
RMSE 是 MSE 的平方根。
RMSE = √MSE
它的優點是量綱與目標變數相同，更易於解釋。與 MSE 一樣，對較大誤差敏感。值越小表示模型性能越好。
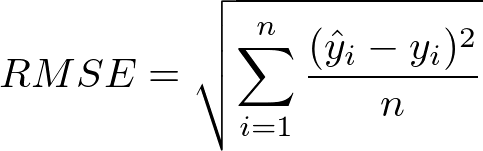
#22
★★★★
平均絕對誤差 (MAE, Mean Absolute Error)
評估指標 (迴歸)
MAE 計算的是預測值與真實值之差的絕對值的平均值。
MAE = (1/n) * Σ|yᵢ - ŷᵢ|
與 MSE/RMSE 相比，MAE 對離群值較不敏感。值越小表示模型性能越好。
>
#23
★★★★★
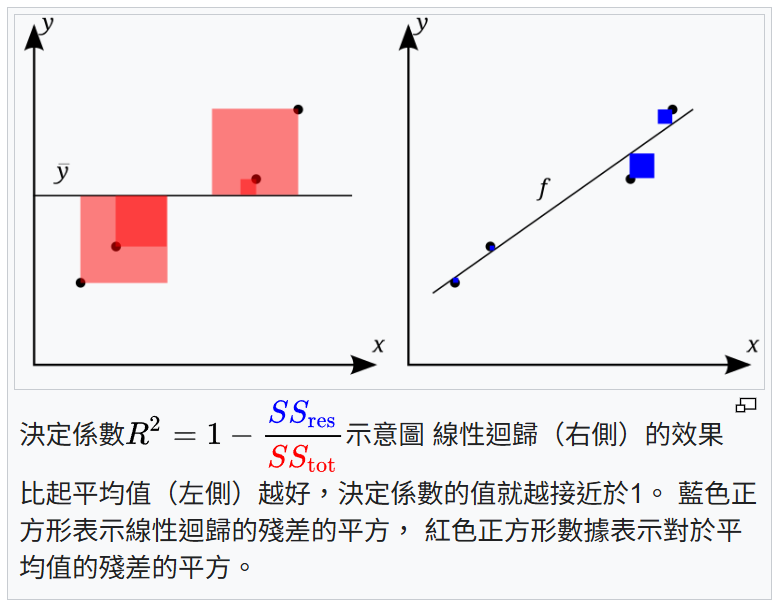
決定係數 (R-squared, R²)
評估指標 (迴歸, 參考樣題 Q14)
R² 衡量的是模型能夠解釋目標變數變異性的比例。其值通常介於 0 到 1 之間（也可能為負）。
R² = 1 - (SSres / SStot) = 1 - (Σ(yᵢ - ŷᵢ)² / Σ(yᵢ - y)²)
(SSres: 殘差平方和, SStot: 總平方和, y: 真實值的平均值)
R² 越接近 1，表示模型對數據的擬合程度越好。但 R² 會隨特徵增加而增加（即使特徵無用），因此有調整後 R²。樣題 Q14 確認 R² 為迴歸模型性能指標。
#24
★★
調整後 R² (Adjusted R-squared)
評估指標 (迴歸)
調整後 R² 在 R² 的基礎上，考慮了模型中自變數（特徵）的數量。當加入無助於解釋目標變數的特徵時，Adjusted R² 通常會下降或增加不多。它對於比較包含不同數量特徵的模型更有用。
#25
★★★★
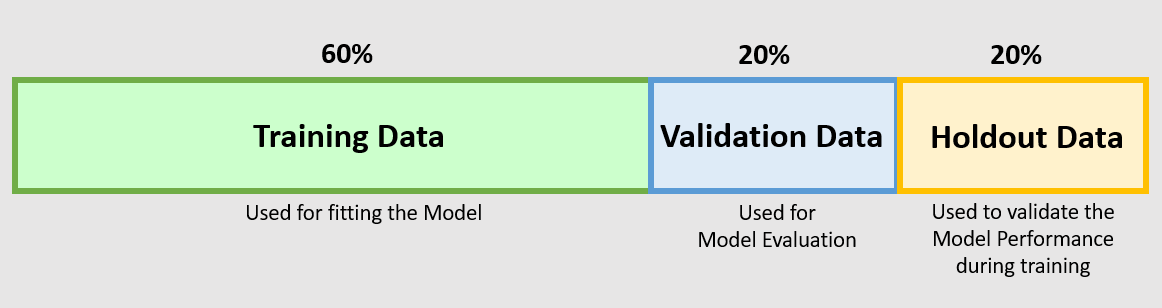
模型驗證方法：Hold-out 驗證
方法說明
最簡單的驗證方法：將數據一次性地劃分為訓練集和驗證集（可能還有測試集）。在訓練集上訓練模型，在驗證集上評估和調整超參數。
  • 優點：簡單、計算成本低。
  • 缺點：評估結果高度依賴於數據劃分的隨機性，特別是在數據量較小時，可能不穩定或有偏差。
#26
★★★★★
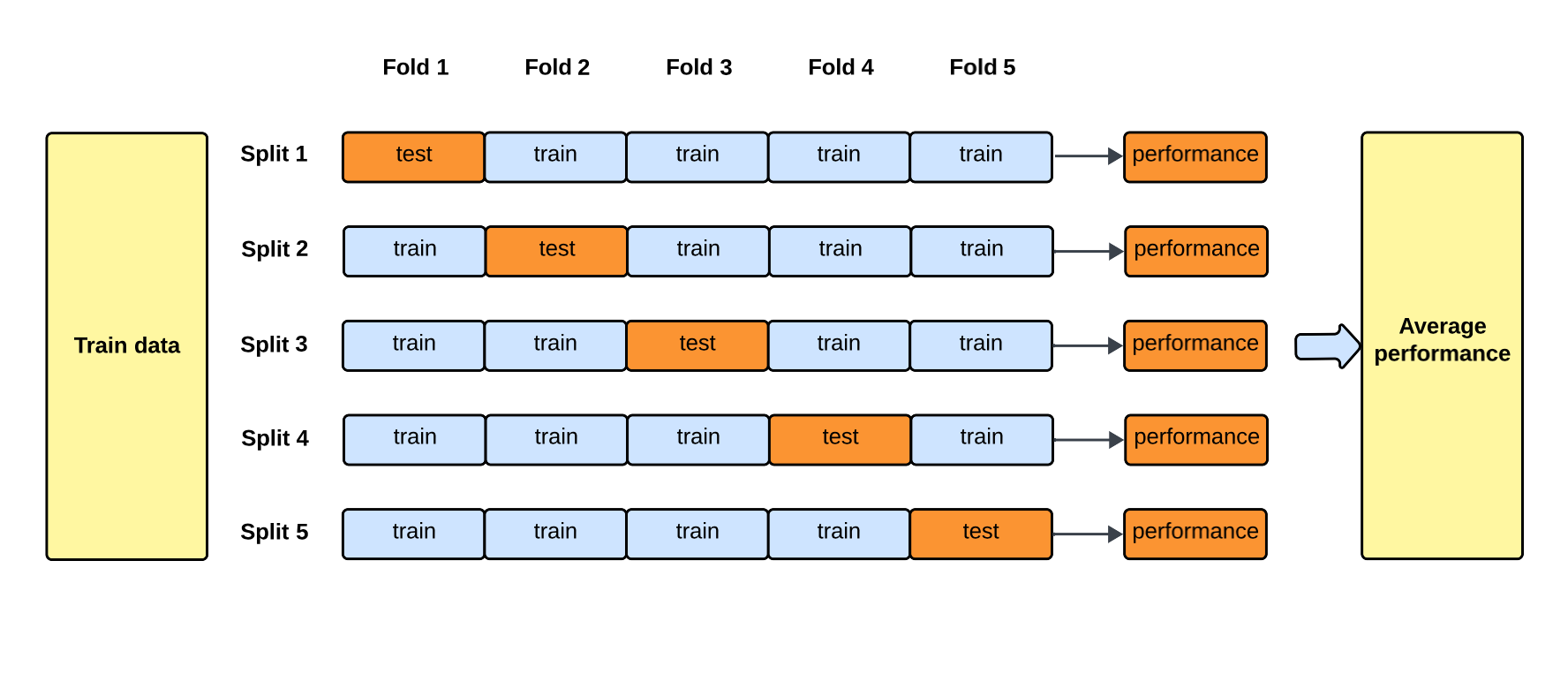
模型驗證方法：交叉驗證 (Cross-Validation, CV)
方法說明 (參考樣題 Q9)
交叉驗證 透過多次劃分數據集，並在不同的劃分上訓練和評估模型，來獲得更可靠的性能估計。最常見的是 K-摺交叉驗證。
  • 優點：評估結果更穩定、偏差更小，能更有效地利用數據，有助於降低過擬合風險（樣題 Q9 確認此點）。
  • 缺點：計算成本比 Hold-out 高，需要訓練 K 個模型。
#27
★★★★
K-摺交叉驗證 (K-Fold Cross-Validation) 的步驟
詳細步驟
  1. 將訓練數據隨機均分為 K 摺。
  2. 進行 K 次迭代：
    • 選定第 i 摺作為驗證集。
    • 其餘 K-1 摺作為訓練集。
    • 在訓練集上訓練模型。
    • 在驗證集上評估模型性能 (Metricᵢ)。
  3. 計算 K 次評估結果的平均值 (Σ Metricᵢ / K) 作為最終性能估計。
常用的 K 為 5 或 10。
#28
★★★
其他交叉驗證變體
變體介紹
除了標準 K-摺，還有：
  • 分層 K-摺 (Stratified K-Fold): 確保每摺類別比例一致，適用於不平衡數據。
  • 留一法 (LOOCV): K=N，計算成本高。
  • 時間序列交叉驗證: 用於時間相關數據，保持時間順序。
需根據數據特性選擇合適的方法。
#29
★★★★★
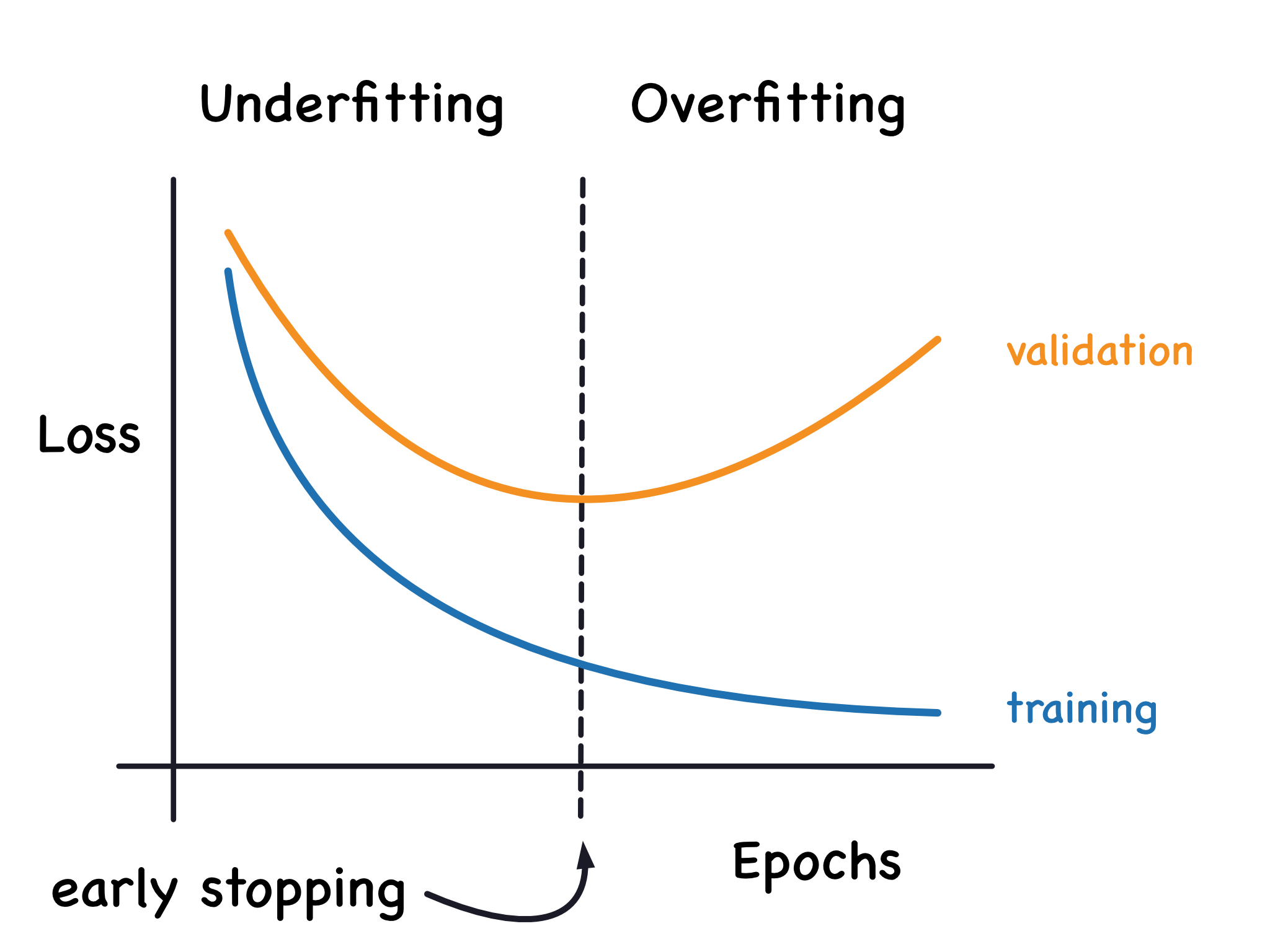
過擬合 (Overfitting) 的診斷 (參考樣題 Q13)
診斷特徵
主要特徵是模型在訓練集上表現很好（訓練誤差低），但在驗證集或測試集上表現差（驗證/測試誤差高）。訓練誤差和測試誤差之間存在顯著差距。樣題 Q13 描述了此情況：訓練誤差低，測試誤差高。
#30
★★★★
欠擬合 (Underfitting) 的診斷
診斷特徵
主要特徵是模型在訓練集和驗證集/測試集上表現都不佳（訓練誤差和驗證/測試誤差都很高）。模型未能捕捉數據的基本模式。
#31
★★★★
使用學習曲線 (Learning Curves) 診斷
診斷方法
繪製訓練誤差和驗證誤差隨訓練樣本量或迭代次數的變化曲線：
  • 過擬合：訓練誤差低，驗證誤差高，兩者差距大。
  • 欠擬合：訓練誤差和驗證誤差都很高，且比較接近。
  • 理想狀態：訓練誤差和驗證誤差都較低，且比較接近。
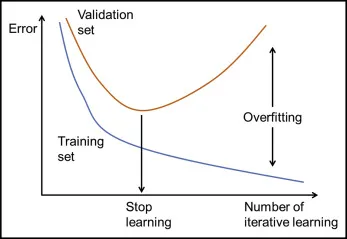
#32
★★★
偏誤-變異數權衡 (Bias-Variance Trade-off) 與擬合狀態
關係
  • 高偏誤 (High Bias) 通常對應欠擬合。
  • 高變異數 (High Variance) 通常對應過擬合。
模型評估與調整的目標是在偏誤和變異數之間找到最佳平衡點。
#33
★★★★★
評估指標選擇：考慮業務目標
核心考量
最重要的考量因素是模型的最終應用場景和業務目標。不同的錯誤類型（假陽性 vs. 假陰性）可能帶來不同的業務成本或風險。應選擇最能反映實際業務需求的指標來指導模型評估和優化。例如，在金融詐欺檢測中，漏掉一個詐欺案例（假陰性）的成本可能遠高於將正常交易誤判為詐欺（假陽性）。
#34
★★★★★
評估指標選擇：考慮類別不平衡 (Class Imbalance)
核心考量
當數據集中不同類別的樣本數量差異很大時（例如，罕見疾病檢測、異常偵測），準確率 (Accuracy) 會變得不可靠。在這種情況下，應優先考慮其他指標：
  • 精確率 (Precision)
  • 召回率 (Recall)
  • F1 分數 (F1 Score)
  • AUC
  • PR 曲線
這些指標更能反映模型在少數類別上的表現。
#35
★★★★
精確率 vs. 召回率 的權衡
權衡關係
精確率和召回率之間通常存在反向關係。提高一個指標往往會導致另一個指標下降（尤其是在調整分類閾值時）。
  • 提高閾值：模型更「嚴格」地預測正類，精確率提高，但可能漏掉更多正類，召回率下降。
  • 降低閾值：模型更「寬鬆」地預測正類，召回率提高，但可能將更多負類誤判為正類，精確率下降。
需要根據業務需求找到合適的平衡點，或使用 F1 分數等綜合指標。
#36
★★★
多分類問題的評估指標
擴展應用
對於三個或更多類別的分類問題，二分類指標可以擴展使用：
  • 宏平均 (Macro Average): 分別計算每個類別的指標（如 Precision, Recall, F1），然後取算術平均值。平等對待每個類別。
  • 微平均 (Micro Average): 匯總所有類別的 TP, FP, TN, FN，然後計算總體指標。受樣本數多的類別影響較大。
  • 加權平均 (Weighted Average): 類似宏平均，但根據每個類別的樣本數進行加權平均。
#37
★★★★
模型比較與基準 (Baseline)
比較方法
在評估一個新模型時，應將其性能與一個或多個基準模型進行比較。基準模型可以是：
  • 簡單規則或啟發式方法。
  • 傳統的、非機器學習的方法。
  • 簡單的機器學習模型（如邏輯回歸、決策樹）。
  • 當前正在使用的模型。
這有助於判斷新模型的實際改進程度和價值。
#38
★★★
模型選擇的考量因素
多維度考量
除了主要的評估指標外，模型選擇還應考慮：
  • 模型複雜度：是否過於複雜難以維護？
  • 訓練時間和推論速度：是否滿足實際應用需求？
  • 可解釋性 (Interpretability)：模型決策過程是否需要被理解？
  • 穩健性 (Robustness)：模型對輸入數據變化的敏感度？
  • 資源需求：訓練和部署所需的計算資源？
需要在這些因素之間進行權衡。(參考 L23302)
#39
★★★
A/B 測試 (A/B Testing)
線上評估
在模型通過離線評估後，常使用 A/B 測試 進行線上評估。將用戶隨機分配到不同組（A 組使用舊模型/無模型，B 組使用新模型），比較兩組在實際業務指標（如點擊率、轉換率、用戶滿意度）上的表現，以驗證新模型在真實環境中的效果。
#40
★★
數據洩漏 (Data Leakage)
常見問題
指在模型訓練過程中無意中使用了來自驗證集或測試集的資訊，或者使用了在預測時點不可用的未來資訊。這會導致模型性能被過於樂觀地估計。在數據劃分和特徵工程階段需要特別小心避免數據洩漏。
#41
★★
模型初始化 (Model Initialization)
訓練考量
神經網路等模型的初始權重設定會影響訓練的收斂速度和最終性能。需要選擇合適的初始化策略（如 Xavier/Glorot 初始化、He 初始化）。
#42
★★
分類閾值選擇 (Threshold Selection)
分類後處理
許多分類模型輸出的是屬於某個類別的機率。需要選擇一個閾值將機率轉換為最終的類別預測（例如，機率 > 0.5 則預測為正類）。閾值的選擇會影響 Precision 和 Recall，應根據業務需求和 ROC/PR 曲線來決定。
#43
★
平均絕對百分比誤差 (MAPE, Mean Absolute Percentage Error)
評估指標 (迴歸)
計算絕對誤差佔真實值的百分比的平均值。優點是無量綱，易於比較不同尺度數據的預測效果。缺點是當真實值接近零時可能不穩定。
#44
★★
交叉驗證中 K 值的選擇
考量因素
K 值越大，訓練集越大，評估結果的偏差越小，但計算成本越高，且變異數可能增大（因為每次迭代的訓練集相似度高）。K=5 或 K=10 是常用的經驗法則，在偏差和計算成本間取得平衡。
#45
★★
模型容量 (Model Capacity)
概念
指模型擬合各種函數的能力。容量過低易導致欠擬合，容量過高易導致過擬合。模型架構、參數數量等都會影響模型容量。
#46
★★
離群值 (Outliers) 對評估指標的影響
影響分析
某些評估指標對離群值比較敏感。例如，在迴歸中，MSE 和 RMSE 受離群值影響較大，而 MAE 較不敏感。在選擇指標時需考慮數據中是否存在離群值及其影響。
#47
★★
模型可部署性 (Deployability)
考量因素
除了性能，還需考慮模型是否容易部署到目標環境（如伺服器、行動裝置）。這涉及模型大小、推論速度、依賴函式庫、與現有系統的整合等。
#48
★
重複隨機子抽樣驗證 (Repeated Random Sub-sampling Validation)
驗證方法
多次隨機地將數據劃分為訓練集和驗證集，計算多次評估結果的平均值。類似於 Hold-out，但透過多次重複來降低單次劃分的隨機性影響。
#49
★
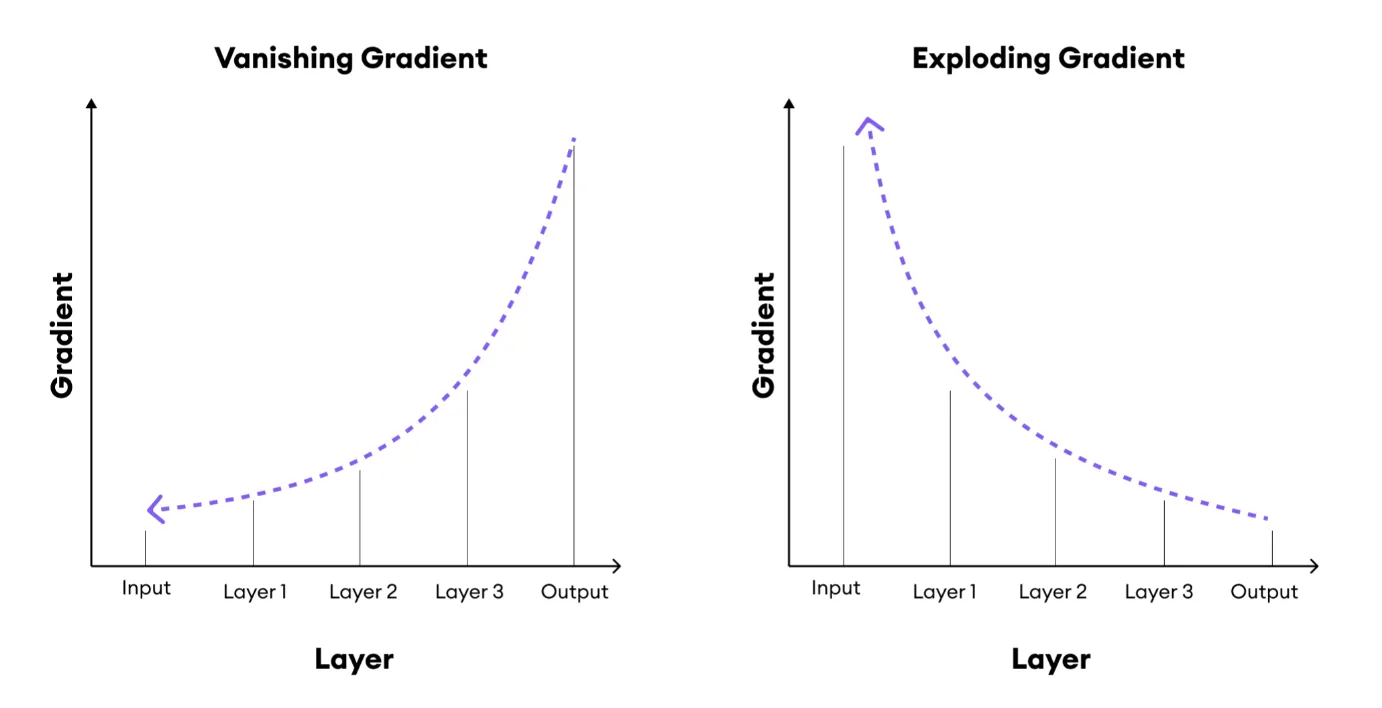
梯度消失 (Vanishing Gradient) 與梯度爆炸 (Exploding Gradient)
訓練問題
深度神經網路訓練中可能出現的問題。梯度消失指梯度在反向傳播中變得非常小，導致淺層網路參數更新緩慢；梯度爆炸指梯度變得非常大，導致訓練不穩定。需要透過合適的激活函數 (如 ReLU)、權重初始化、梯度裁剪等方法解決。
#50
★
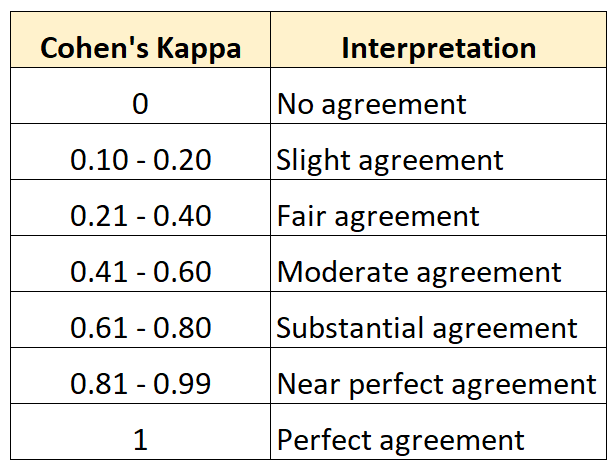
Kappa 係數 (Cohen's Kappa)
評估指標 (分類)
衡量分類一致性的指標，考慮了隨機一致性的可能性。用於評估模型預測與實際類別的一致程度，或不同評分者之間的一致性。
#51
★
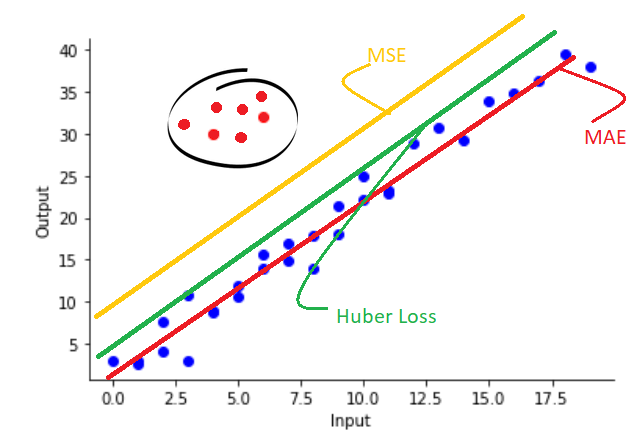
Huber 損失 (Huber Loss)
損失函數 (迴歸)
一種結合了 MSE 和 MAE 特點的損失函數。對於較小的誤差，表現類似 MSE（平方）；對於較大的誤差，表現類似 MAE（線性）。對離群值的敏感度介於兩者之間。
#52
★
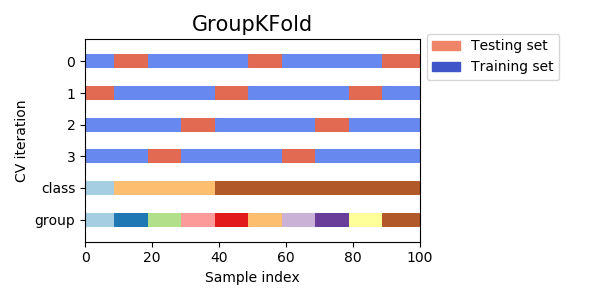
組 K-摺交叉驗證 (Group K-Fold)
交叉驗證變體
確保來自同一組（例如，同一使用者、同一病人）的所有樣本同時出現在訓練集或驗證集中，而不會分散在兩者之間。用於處理數據中存在組結構，避免資訊洩漏。
#53
★
噪聲 (Noise) 對擬合的影響
影響分析
訓練數據中的隨機噪聲是導致模型過擬合的原因之一。模型可能會學習噪聲而非潛在的真實模式。
#54
★
多指標優化 (Multi-metric Optimization)
優化考量
在某些情況下，可能需要同時優化多個評估指標（例如，同時考慮精確率和召回率，或同時考慮性能和公平性）。這通常需要定義一個綜合指標或使用多目標優化技術。
#55
★
模型可監控性 (Monitorability)
考量因素
模型是否易於監控其在部署後的性能、輸入數據分佈變化、潛在偏差等。選擇易於監控的模型或設計相應的監控機制對於維護模型效果至關重要。
#56
★
確保數據劃分的隨機性
實踐細節
在劃分訓練/驗證/測試集或進行交叉驗證時，通常需要先將數據隨機打亂，以避免因數據原始順序（例如，按時間排序）導致劃分偏差。但對於時間序列數據則需特殊處理。
#57
★★
對數損失 (Log Loss)
評估指標 (分類)
與交叉熵損失密切相關，衡量的是模型預測機率的準確性。對於預測錯誤且置信度高的情況會給予較大的懲罰。值越小越好。
#58
★
交叉驗證的計算複雜度
成本考量
K-摺交叉驗證需要訓練 K 個模型，其總計算成本約為在整個數據集上訓練單個模型的 K 倍。因此在選擇 K 值和應用交叉驗證時需考慮計算資源限制。
#59
★
提升圖 (Lift Chart) 與 增益圖 (Gain Chart)
評估工具 (分類)
用於評估模型相對於隨機選擇或無模型的性能提升程度。常用於目標行銷等場景，衡量模型在識別潛在客戶方面的有效性。
#60
★
模型版本控制 (Model Versioning)
實踐考量
如同程式碼需要版本控制一樣，對訓練好的模型及其相關的元數據（如訓練數據、超參數、性能指標）進行版本控制，有助於追蹤、比較不同版本的模型，以及在需要時回滾到先前版本。
沒有找到符合條件的重點。
↑