iPAS AI應用規劃師 考試重點
L23103 數值優化技術與方法
主題分類
1
優化基本概念與目標
2
損失函數的角色
3
梯度下降法原理
4
梯度下降法變體 (SGD, Mini-batch)
5
學習率與收斂性
6
進階優化器 (Momentum, Adam 等)
7
優化挑戰與正則化
8
凸優化與非凸優化簡介
#1
★★★★★
數值優化 (Numerical Optimization) 在機器學習中的角色
核心概念
在機器學習中,數值優化是指尋找一組模型參數(如神經網路的權重、線性迴歸的係數),使得某個預先定義的目標函數達到最小值(或最大值)的過程。這個目標函數通常是衡量模型預測錯誤程度的損失函數 (Loss Function) 或成本函數 (Cost Function)。
#2
★★★★
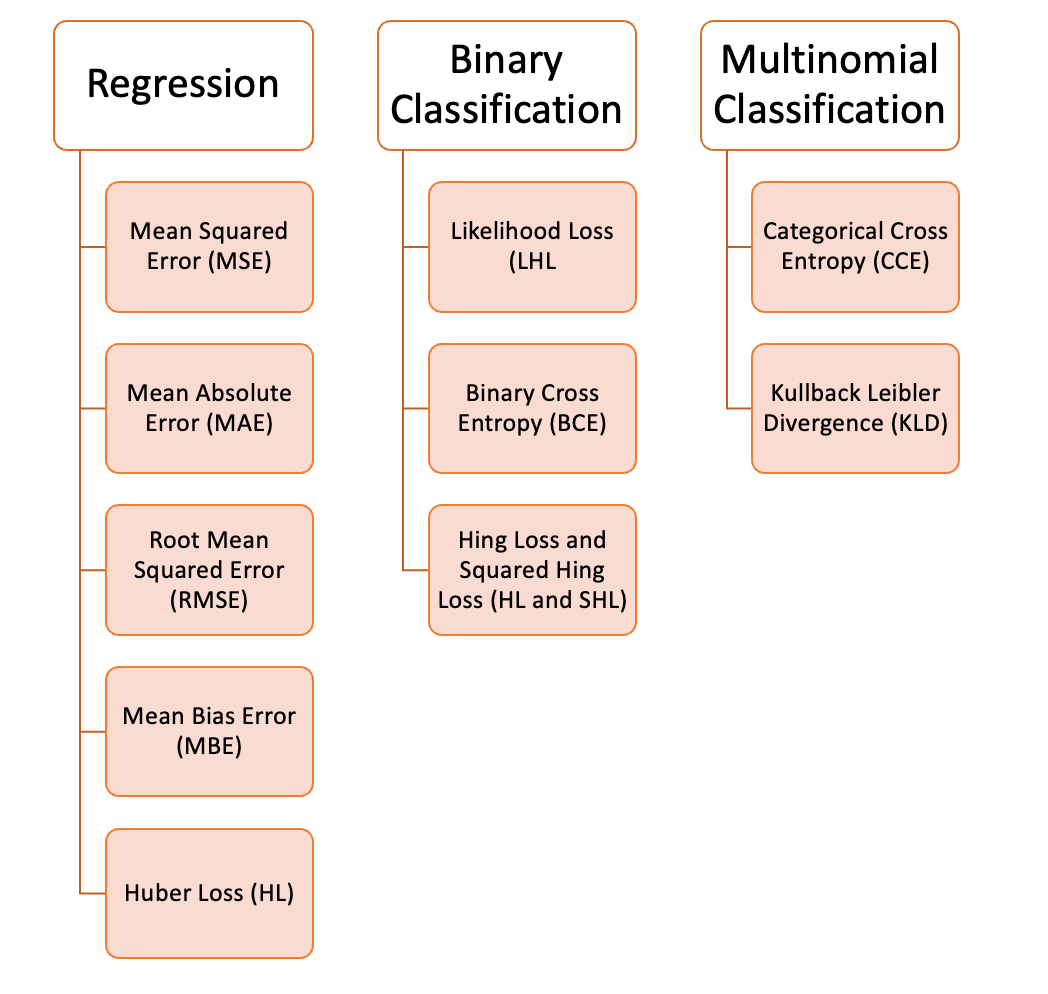
目標函數 (Objective Function) / 準則 (Criterion)
核心術語
目標函數是我們希望最小化或最大化的函數。在典型的機器學習訓練中,目標函數通常是損失函數或成本函數,代表了模型的預測誤差。
#3
★★★
最小化 vs. 最大化
優化方向
大多數機器學習優化問題被表述為最小化問題(例如,最小化預測誤差)。最大化問題(例如,最大化似然函數)可以透過對目標函數取負號轉換為最小化問題。因此,優化演算法通常關注如何找到最小值點。
#4
★★★★
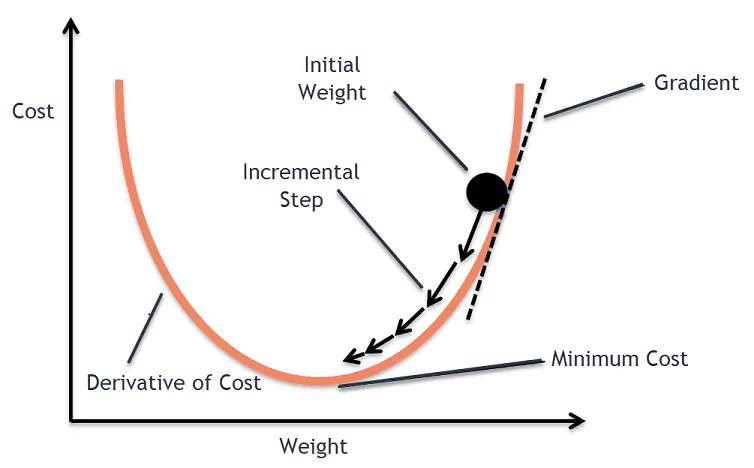
迭代優化 (Iterative Optimization)
核心思想
許多數值優化方法,特別是在機器學習中,採用迭代的方式。從一個初始參數值開始,逐步更新參數,每次更新都試圖使目標函數值更接近最優值(通常是更小),直到滿足某個停止條件(如達到最大迭代次數、目標函數值變化很小)。梯度下降法就是一種典型的迭代優化方法。

#5
★★★★★
損失函數 (Loss Function) 在優化中的角色
核心作用
損失函數是數值優化的目標。它量化了模型當前參數下的預測結果與真實數據之間的差異。優化演算法的任務就是調整模型參數,以找到使損失函數值最小的那組參數。
#6
★★★★
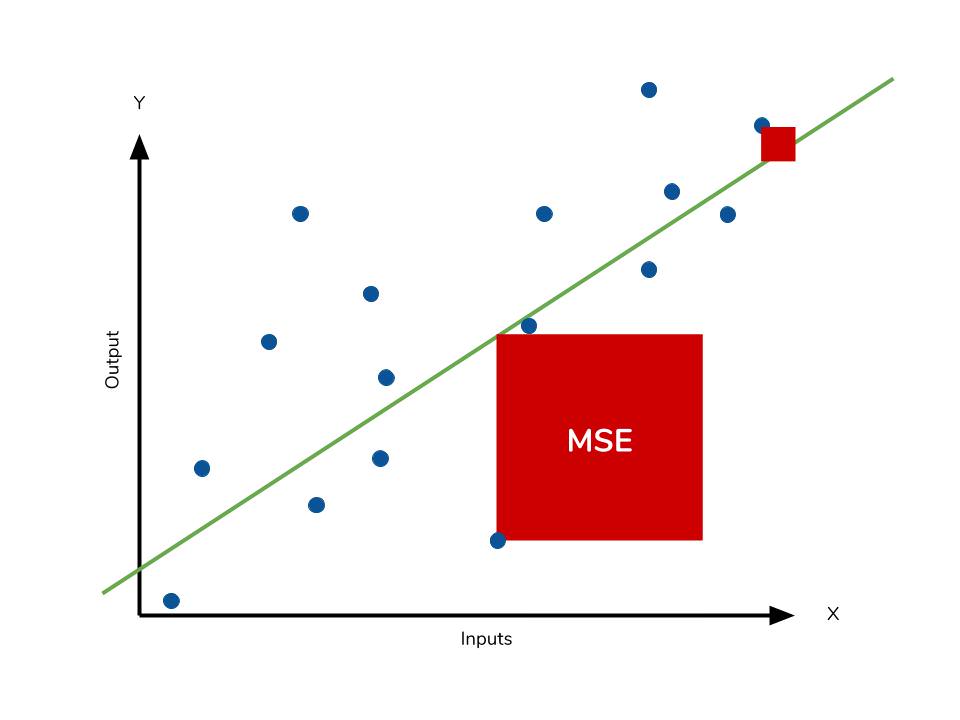
常見損失函數:均方誤差 (MSE, Mean Squared Error)
迴歸常用
常用於迴歸問題。計算預測值與真實值之差的平方的平均值。優化目標是最小化 MSE。對較大誤差懲罰較重。
#7
★★★★
常見損失函數:交叉熵損失 (Cross-Entropy Loss)
分類常用
常用於分類問題,特別是當模型輸出為機率時。它衡量模型預測的機率分佈與真實標籤的機率分佈之間的差異。優化目標是最小化交叉熵損失。

#8
★★★
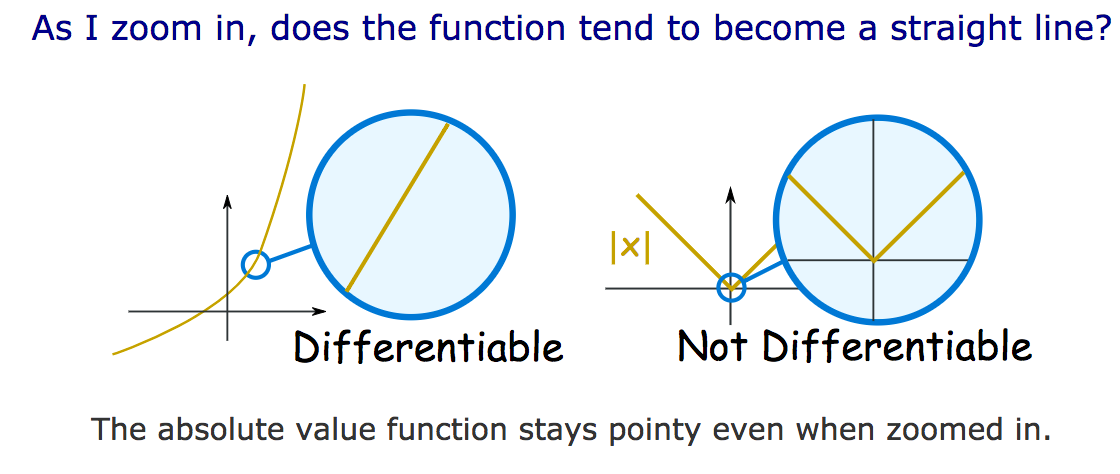
損失函數的可微分性 (Differentiability)
重要性質
對於基於梯度的優化方法(如梯度下降法),損失函數必須是可微分的(或至少是次可微的),這樣才能計算出梯度來指導參數更新的方向。大多數常用的損失函數(如 MSE、交叉熵)都滿足這個條件。
#9
★★★★★
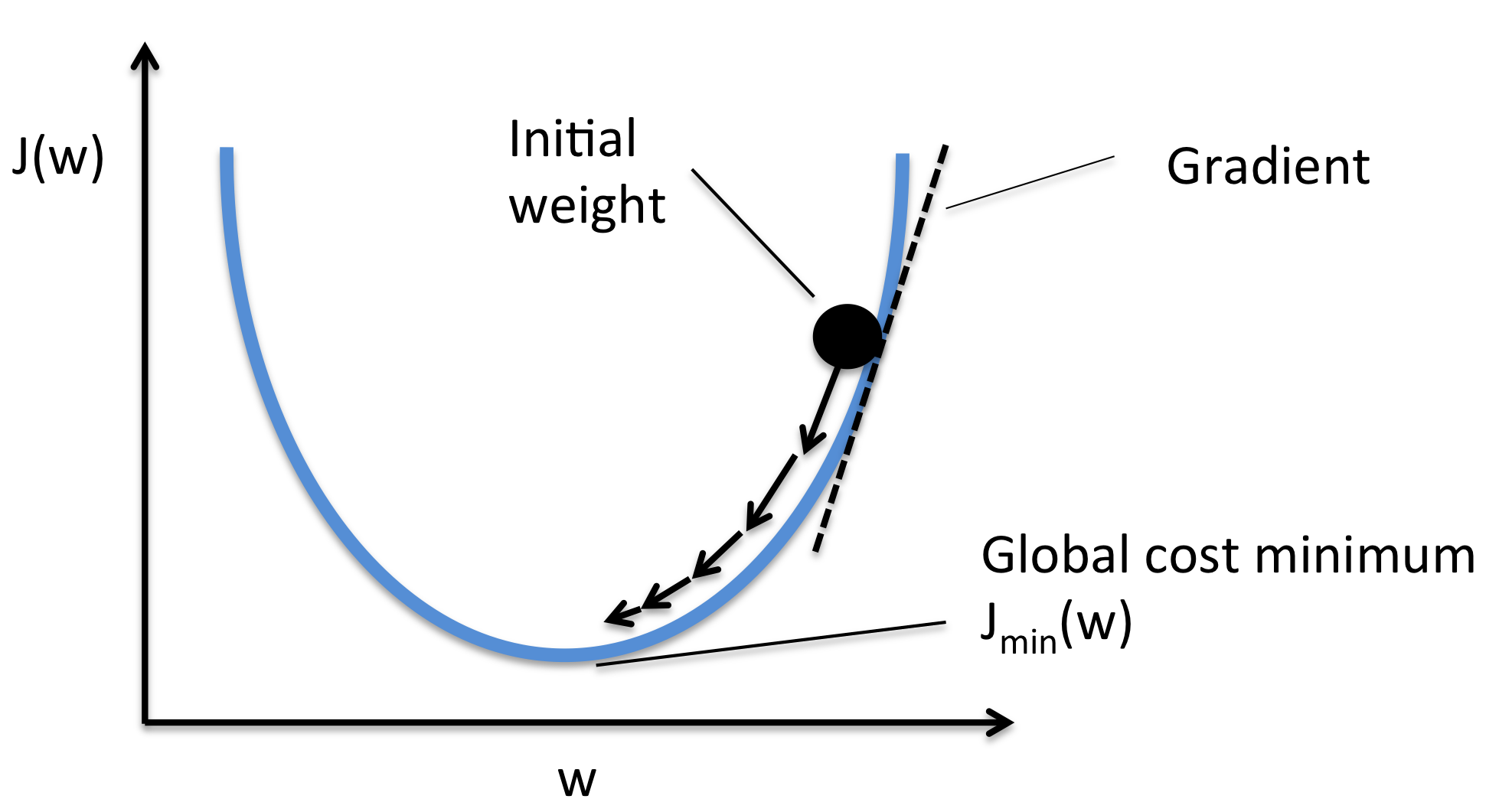
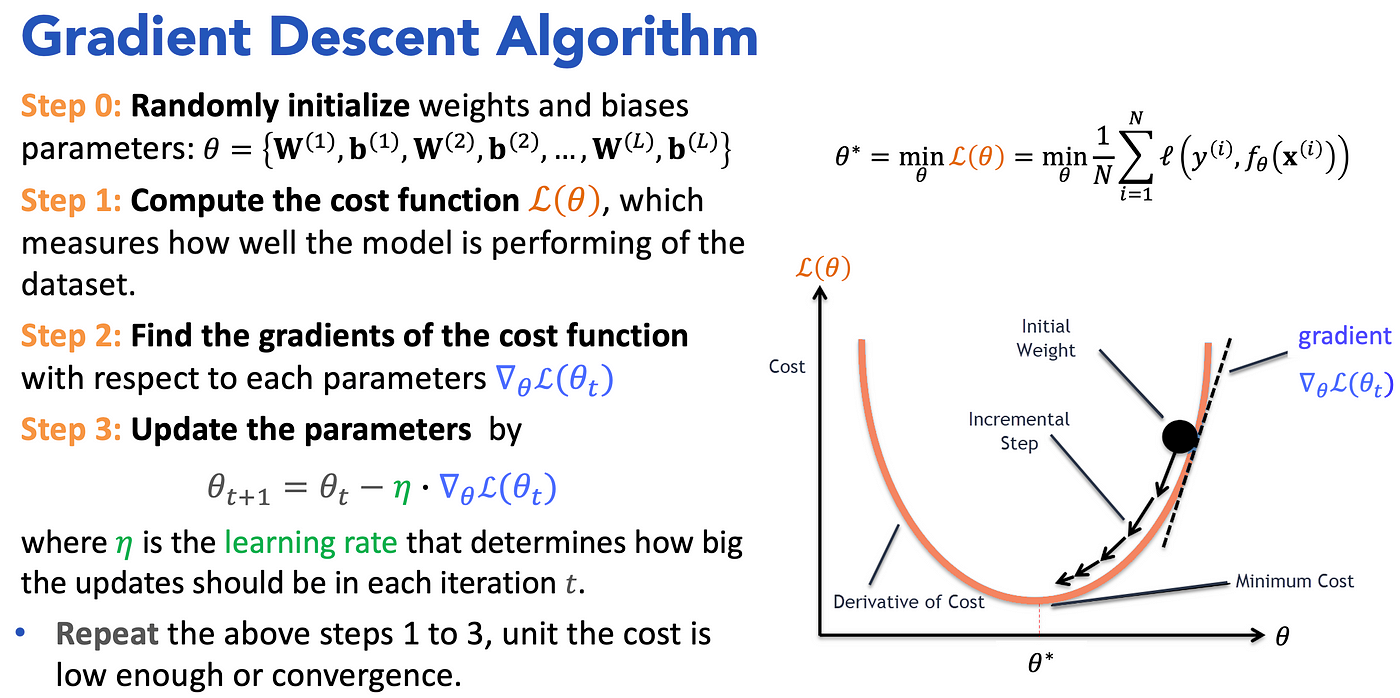
梯度下降法 (Gradient Descent, GD) - 核心思想
核心原理
梯度下降法是最基本也是最重要的優化演算法之一。它利用了目標函數(損失函數)的梯度訊息。梯度指向函數值上升最快的方向,因此梯度的負方向就是函數值下降最快的方向。演算法從初始參數開始,反覆沿著負梯度方向更新參數,以逐步接近最小值點。
#10
★★★★★
梯度 (Gradient) 的概念
數學基礎
對於一個多元函數(如損失函數,其變數是模型參數),梯度是一個向量,由函數對每個變數(參數)的偏導數組成。它表示了函數在某一點變化最快的方向和速率。∇L(θ) = [∂L/∂θ₁, ∂L/∂θ₂, ..., ∂L/∂θn]。

#11
★★★★★
梯度下降法的更新規則
核心公式
參數 θ 在第 t+1 次迭代的更新公式為:
θt+1 = θt - η * ∇L(θt)
其中:
θt+1 = θt - η * ∇L(θt)
其中:
- θt:第 t 次迭代的參數值。
- η (eta):學習率 (Learning Rate),控制更新步長。
- ∇L(θt):損失函數 L 在 θt 處的梯度。
#12
★★★★
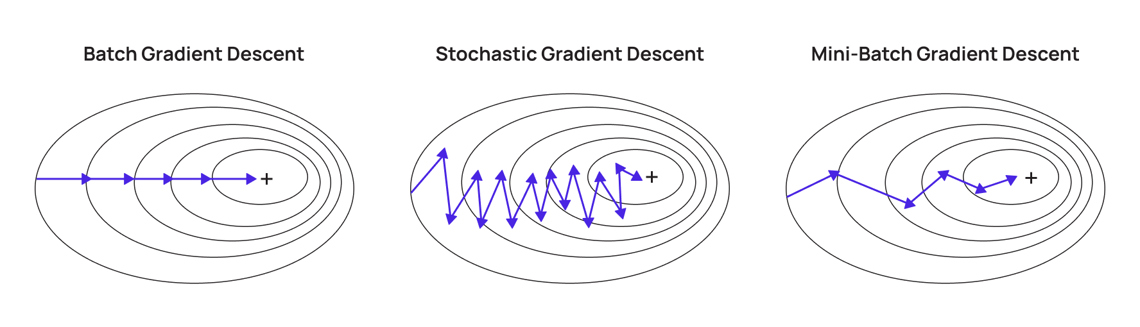
批次梯度下降法 (Batch Gradient Descent, BGD)
GD 類型
BGD 在每次參數更新時,使用整個訓練集的數據來計算損失函數的梯度。
- 優點:梯度計算準確,收斂方向穩定。
- 缺點:對於大規模數據集,每次迭代計算成本非常高,訓練速度慢,可能無法載入內存。
#13
★★★★★
隨機梯度下降法 (SGD, Stochastic Gradient Descent)


GD 變體
SGD 在每次參數更新時,僅隨機選擇一個訓練樣本來計算梯度。
- 優點:更新速度快,計算成本低,適用於大規模數據集,梯度隨機性有助於跳出局部最小值。
- 缺點:梯度估計噪聲大,收斂過程可能震盪,不一定能精確收斂到最小值。

#14
★★★★★
小批量梯度下降法 (Mini-batch Gradient Descent)
GD 變體
小批量梯度下降是介於 BGD 和 SGD 之間的折衷方案。在每次參數更新時,使用一小批 (mini-batch) 隨機樣本(例如 32, 64, 128 個樣本)來計算梯度。
- 優點:結合了 BGD 的穩定性和 SGD 的效率。能夠利用現代硬體(如 GPU)的並行計算能力。收斂過程比 SGD 更穩定。
- 是目前深度學習和大規模機器學習中最常用的梯度下降變體。

#15
★★★
SGD/Mini-batch 的隨機性優勢
優勢分析
由於每次更新使用的數據子集不同,SGD 和 Mini-batch 的梯度估計帶有噪聲。這種噪聲有時反而有益,因為它可以幫助優化過程跳出損失函數的局部最小值 (Local Minima) 或鞍點 (Saddle Points),增加找到更好解的可能性。
 >
>
 >
>

#16
★★★★★
學習率 (Learning Rate, η) 的作用與影響
關鍵超參數
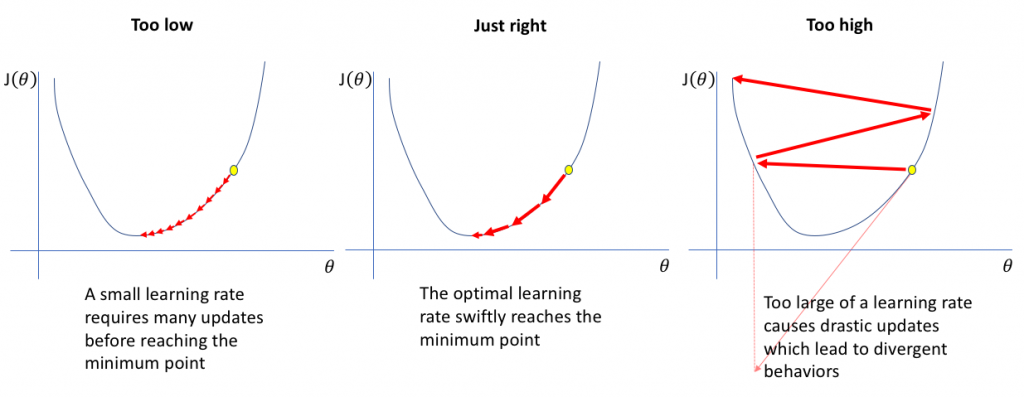
學習率控制梯度下降中每一步更新的幅度。它是最重要的超參數之一。
- 學習率過高:可能導致更新步長太大,越過最小值點,在最小值附近震盪甚至發散,無法收斂。
- 學習率過低:導致更新步長太小,收斂速度非常緩慢,可能需要極長的訓練時間,也更容易陷入不良的局部最小值。

#17
★★★★
收斂 (Convergence) 的概念
訓練狀態
在迭代優化中,收斂是指演算法達到一個穩定狀態,參數值不再發生顯著變化,或者目標函數值(損失)不再顯著下降,接近某個(可能是局部的)最小值。判斷是否收斂通常基於損失變化、梯度大小或迭代次數。
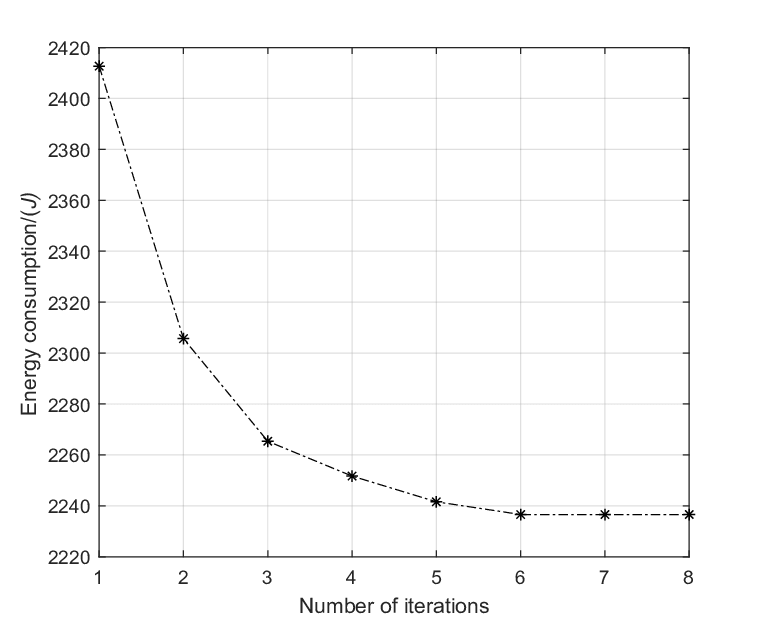
#18
★★★
學習率調整策略:學習率衰減/排程 (Learning Rate Decay/Scheduling)
常見策略
為了在訓練初期快速下降、後期穩定收斂,常常在訓練過程中動態調整學習率。常見策略包括:
- 按步衰減 (Step Decay): 每隔一定輪數降低學習率。
- 指數衰減 (Exponential Decay): 學習率按指數級逐漸減小。
- 基於性能衰減 (Plateau Decay): 當驗證集性能不再提升時降低學習率。
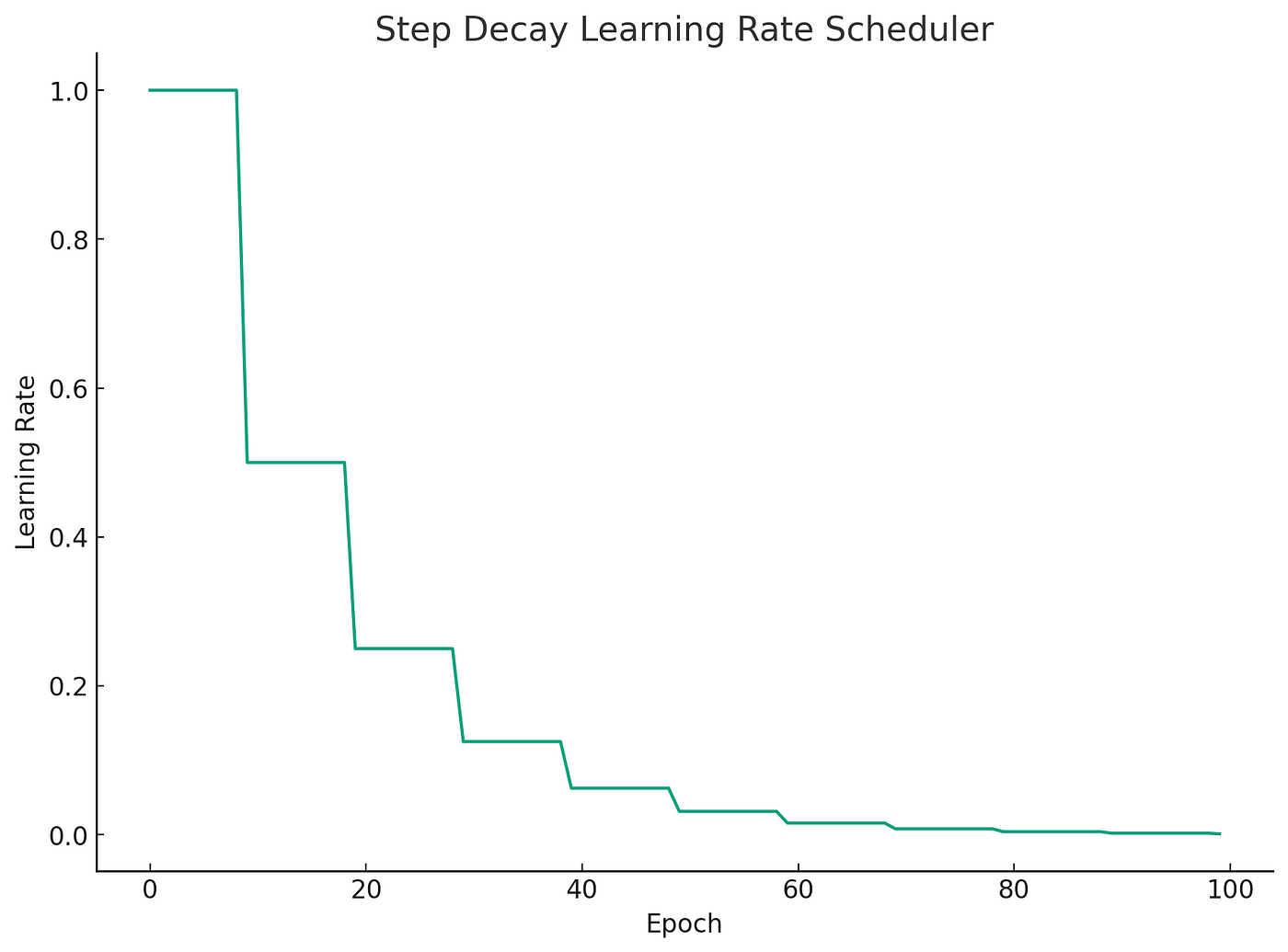
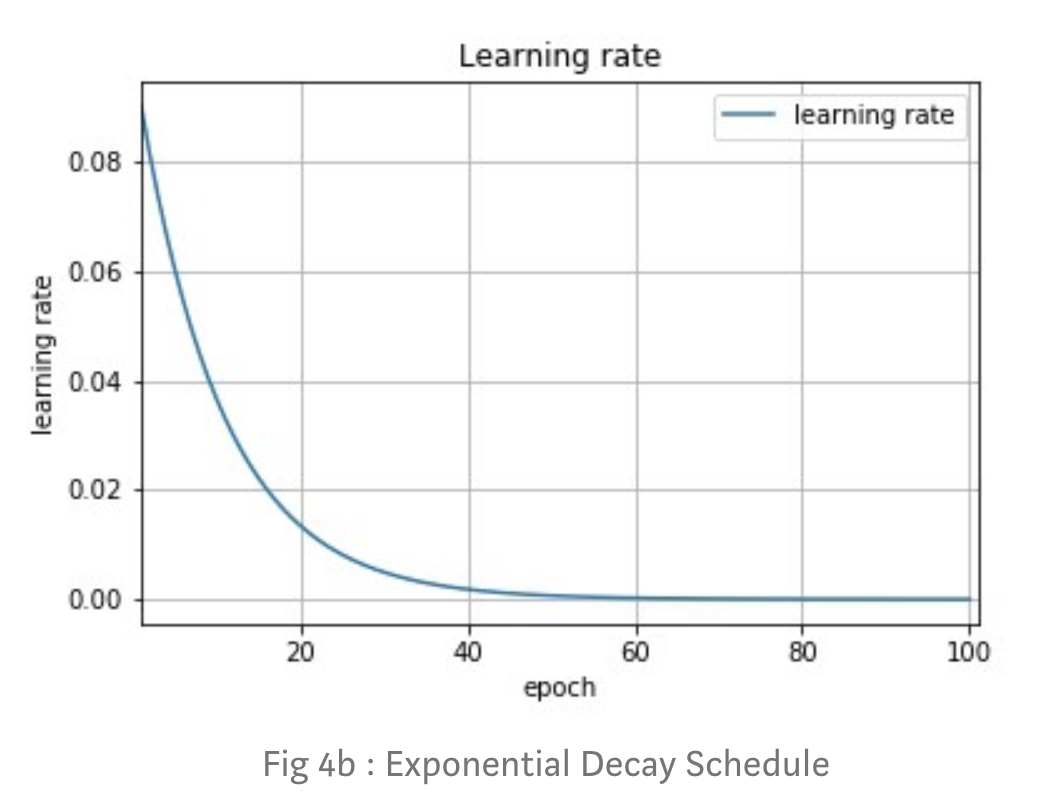
#19
★★
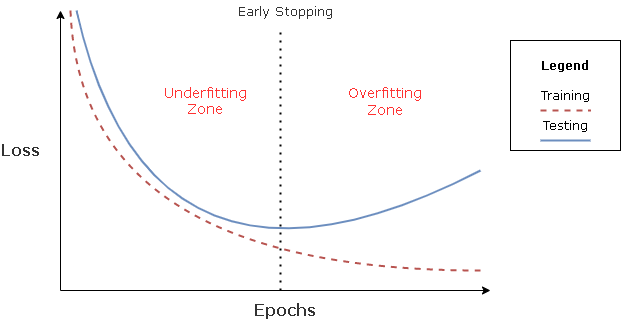
監控收斂過程:損失曲線 (Loss Curve)
監控方法
繪製訓練損失和驗證損失隨訓練迭代次數(或輪數)變化的曲線,是監控優化過程、判斷收斂狀態以及診斷過擬合/欠擬合的重要工具。理想情況下,兩條曲線都應下降並收斂到較低水平。
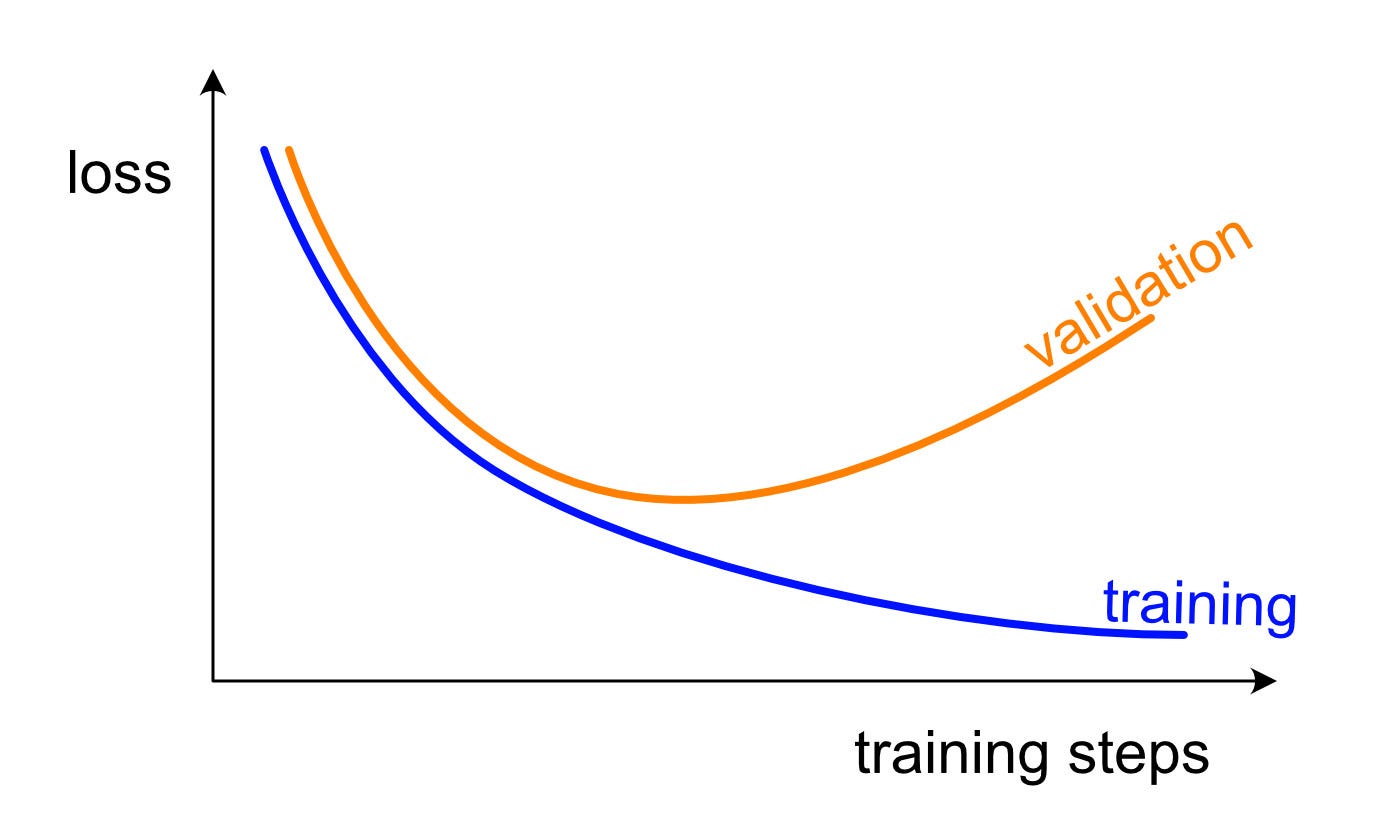
#20
★★★★
動量 (Momentum) 優化


進階優化技術
動量法通過累積先前梯度的指數加權移動平均,來加速梯度下降在相關方向上的前進速度,並抑制無關方向的震盪。這有助於更快地收斂,並可能衝過淺的局部最小值或鞍點。動量係數(通常接近 1,如 0.9)是一個超參數。
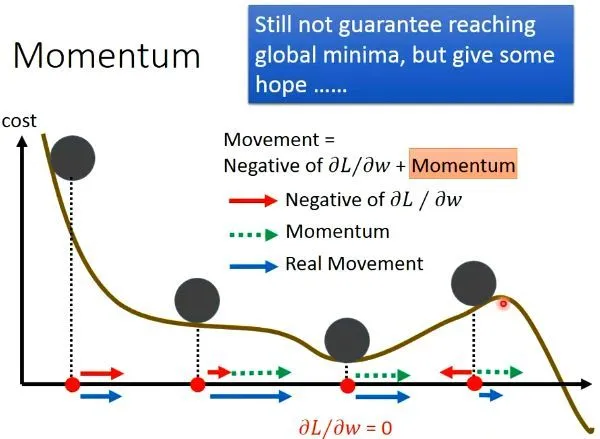
#21
★★★
Nesterov 加速梯度 (NAG, Nesterov Accelerated Gradient)
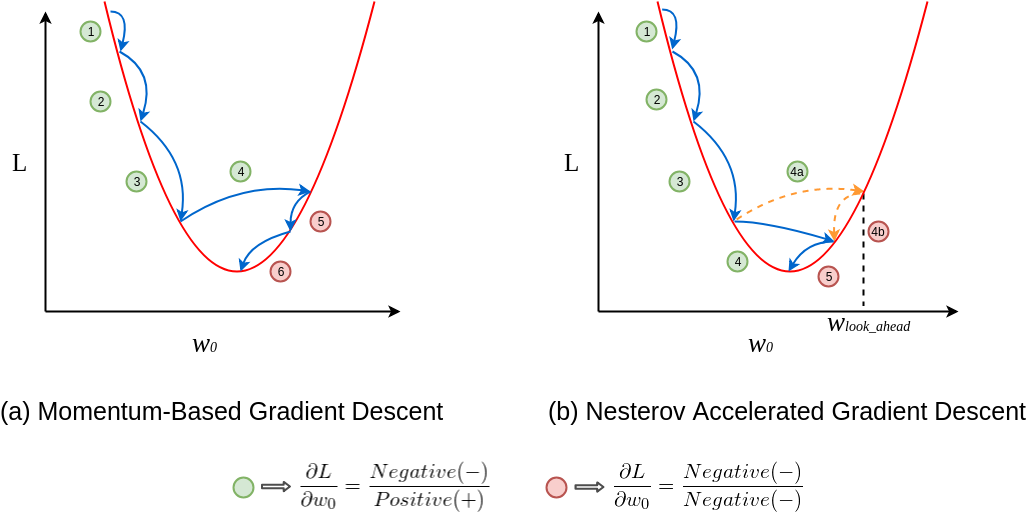
動量法的改進
NAG 是對標準動量法的一種改進。它在計算梯度之前,先「預見性」地根據累積的動量估計下一步參數的位置,然後在該預估位置計算梯度。這種「向前看」的策略通常能提供更好的收斂性。
#22
★★★★
自適應學習率 (Adaptive Learning Rates) 概念
核心思想
傳統梯度下降對所有參數使用相同的學習率。自適應學習率方法則為每個參數維護一個獨立的學習率,並根據該參數過去的梯度訊息自動調整。基本思想是:對於更新頻繁或梯度較大的參數,降低其學習率;對於更新稀疏或梯度較小的參數,提高其學習率。
#23
★★★
Adagrad (Adaptive Gradient Algorithm)
自適應優化器
Adagrad 根據參數過去所有梯度的平方和來調整學習率。梯度累計越多(更新越頻繁)的參數,其學習率會越小。缺點是學習率會持續單調下降,可能在訓練後期變得過小。
#24
★★★★
RMSprop (Root Mean Square Propagation)
自適應優化器
RMSprop 旨在解決 Adagrad 學習率過早衰減的問題。它使用梯度的平方的指數加權移動平均來調整學習率,而不是累加所有歷史梯度。這使得學習率可以適應近期梯度的大小。
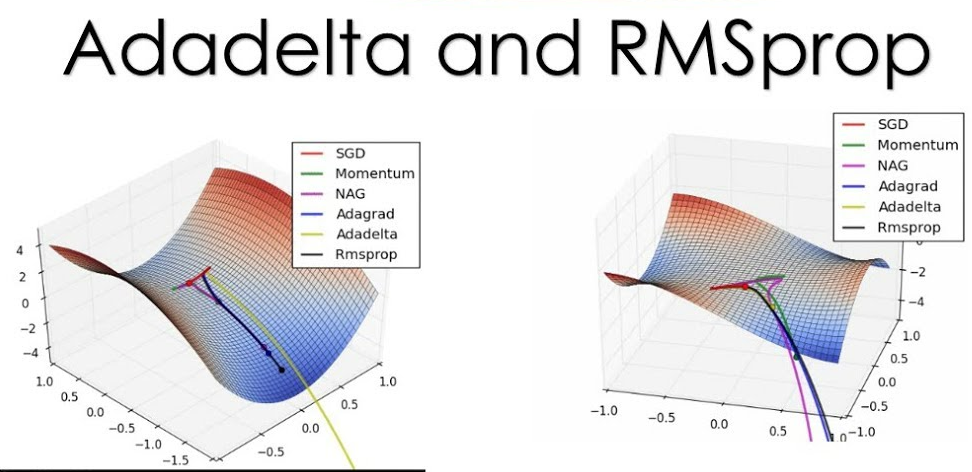
#25
★★★★★
Adam (Adaptive Moment Estimation)
常用自適應優化器
Adam 是目前最流行和廣泛使用的優化演算法之一。它結合了動量法和 RMSprop 的思想:
- 使用梯度的指數加權移動平均(一階動量估計)。
- 使用梯度平方的指數加權移動平均(二階動量估計)來調整學習率。
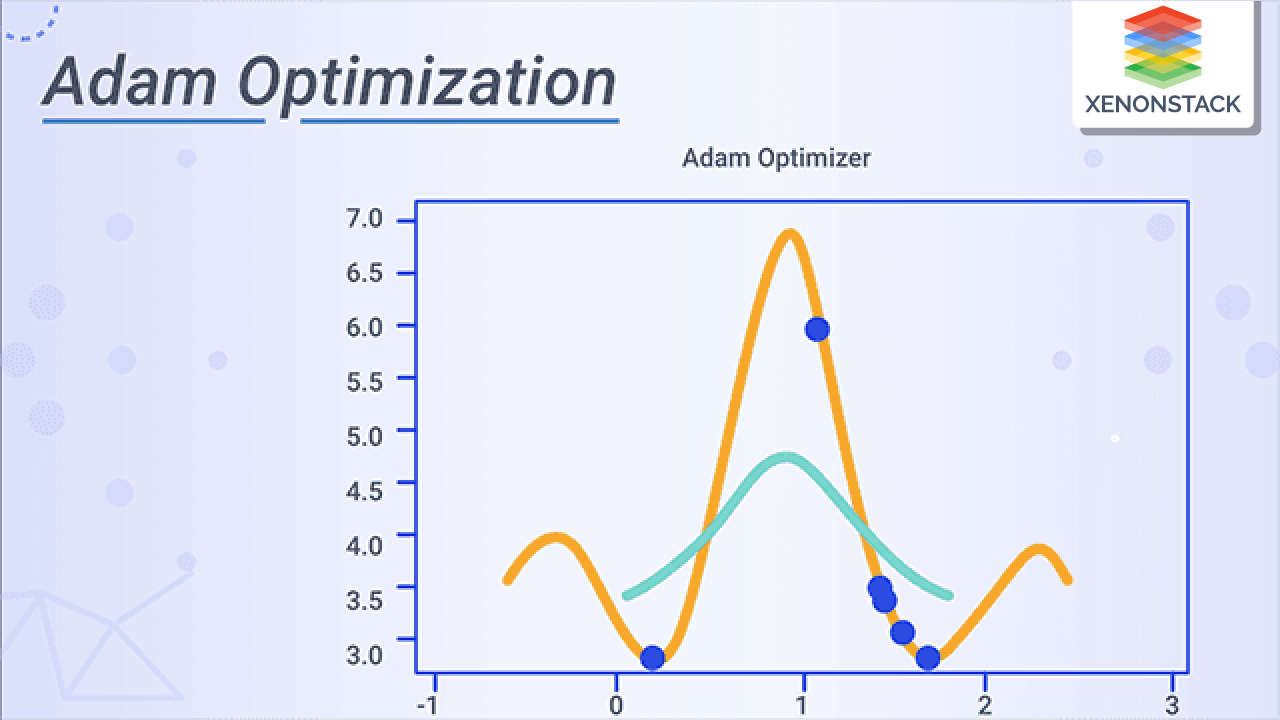
#26
★★★★
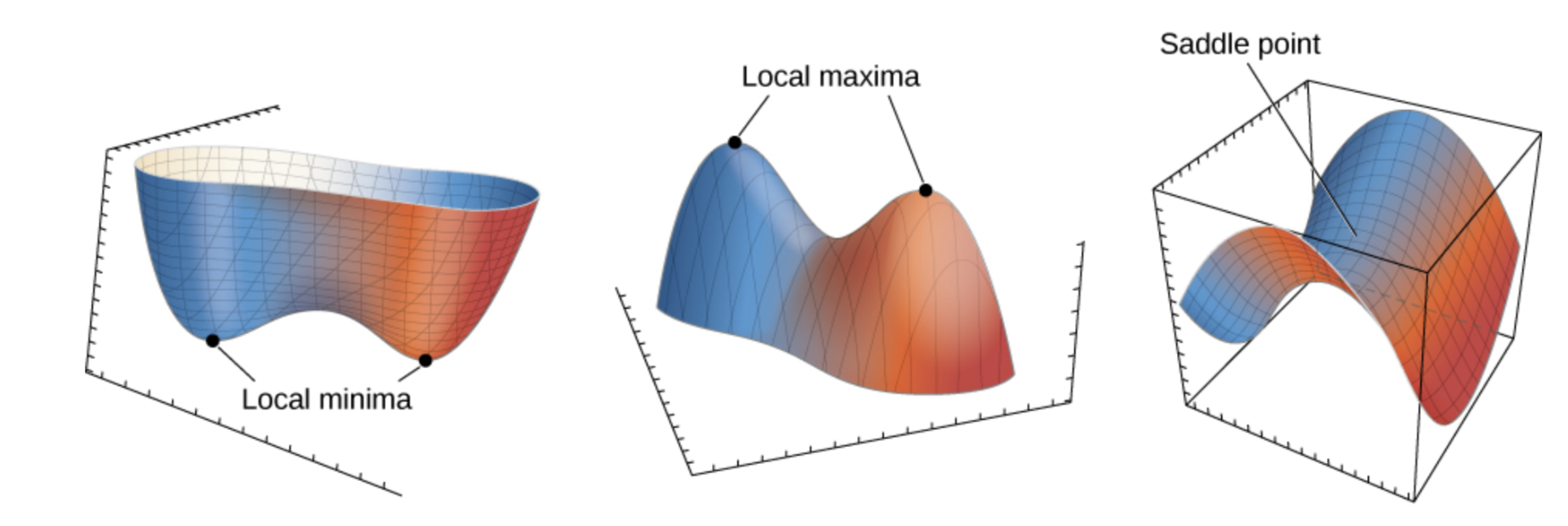
優化挑戰:局部最小值 (Local Minima)
挑戰說明
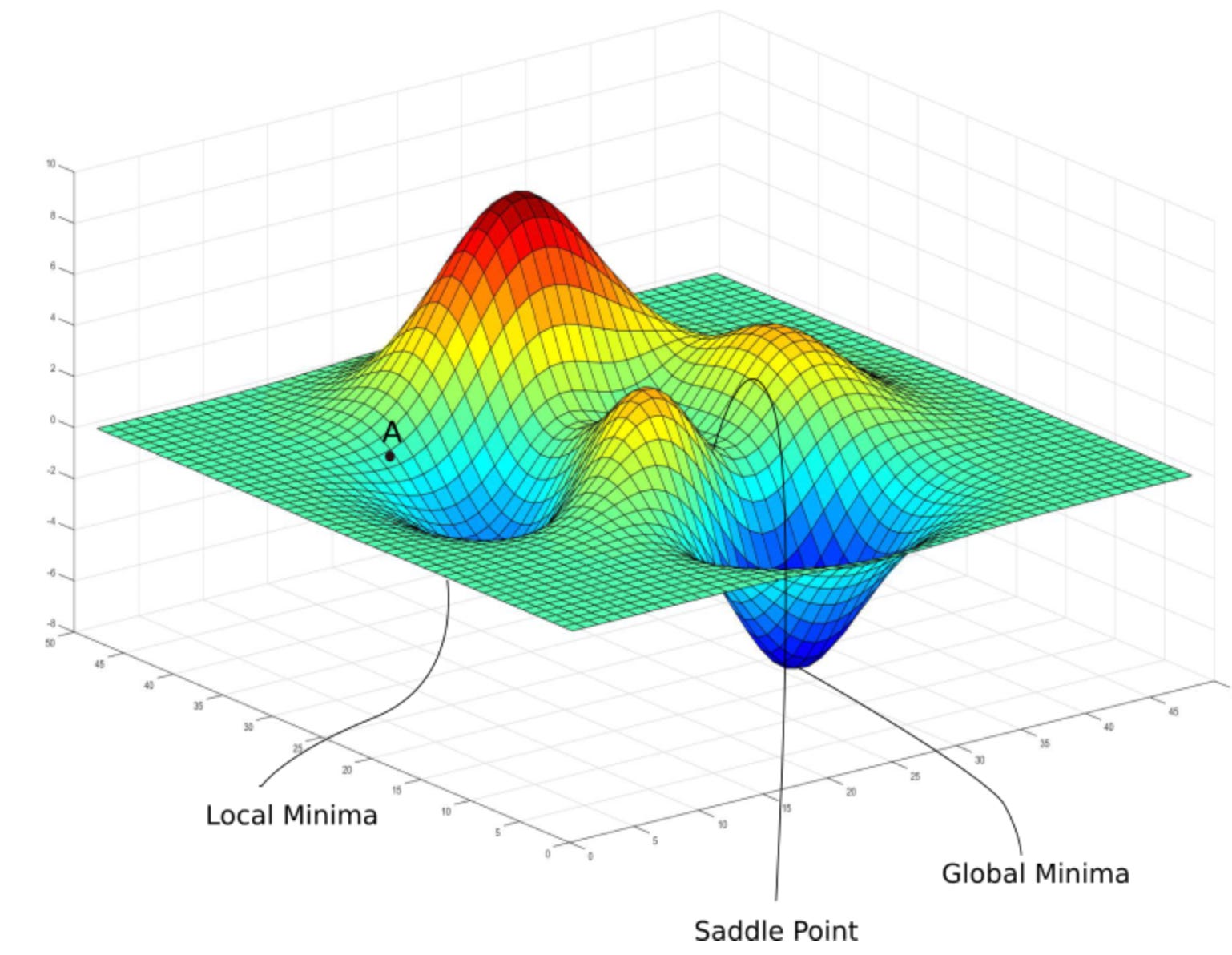
對於非凸 (Non-convex) 的損失函數(常見於深度學習),梯度下降法只能保證收斂到一個局部最小值(或鞍點),而不一定是全局最小值 (Global Minimum)。即找到的解可能不是最佳解。

#27
★★★
優化挑戰:鞍點 (Saddle Points)
挑戰說明
鞍點是指在某個點,函數在某些維度上是局部最小值,但在另一些維度上是局部最大值。在鞍點處,梯度為零,可能導致梯度下降法停滯不前。在高維優化問題中(如深度學習),鞍點問題比局部最小值問題更常見。動量法和自適應優化器有助於逃離鞍點。

#28
★★
優化挑戰:梯度消失 (Vanishing Gradients) 與 梯度爆炸 (Exploding Gradients)
深度學習挑戰
在訓練深層神經網路時,梯度在反向傳播過程中可能逐層指數級減小(消失)或增大(爆炸)。
- 梯度消失:導致淺層網路參數更新緩慢,難以訓練。
- 梯度爆炸:導致訓練不穩定,損失值變為 NaN。
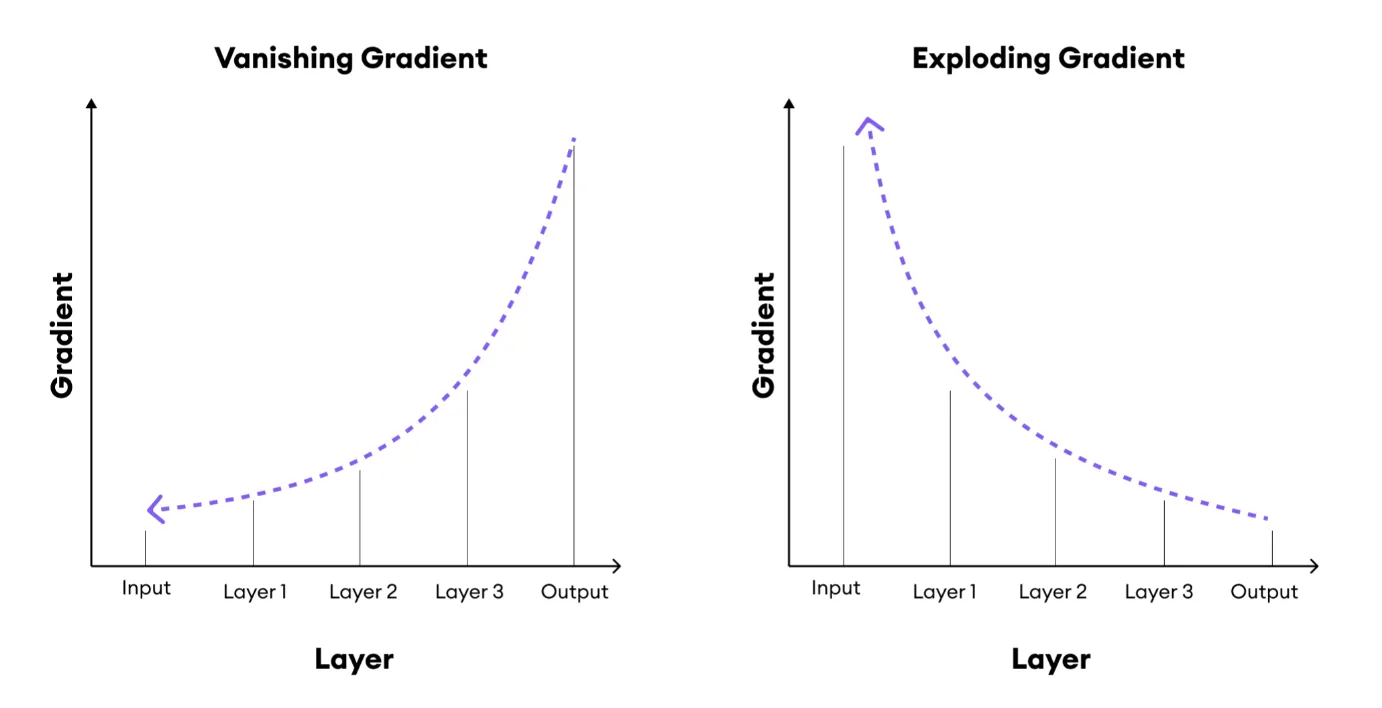
#29
★★★★
正則化 (Regularization) 與優化的關係 (參考樣題 Q3)
關係說明
正則化(如 L1, L2)是透過修改目標函數(在損失函數中加入懲罰項)來影響優化過程的。優化演算法現在需要最小化這個包含懲罰項的新目標函數,這會引導參數朝著更簡單、更不易過擬合的方向進行優化。樣題 Q3 表明正則化用於降低過擬合。
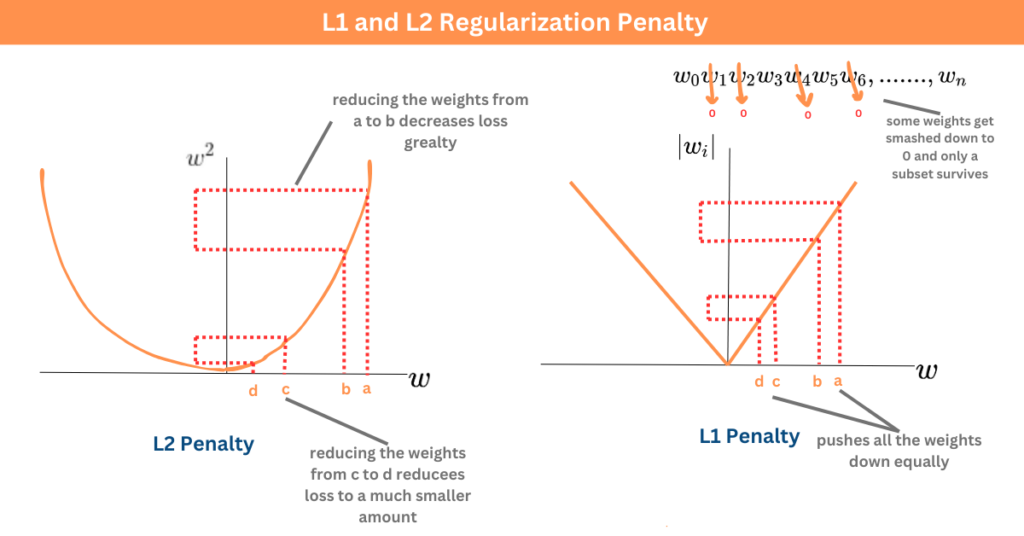
#30
★★★★
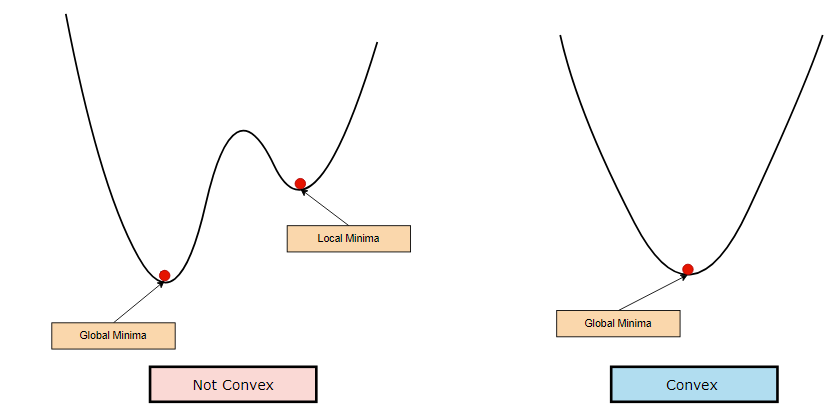
凸優化 (Convex Optimization)
優化類型
如果目標函數是凸函數,並且可行域是凸集,則該優化問題是凸優化問題。
- 關鍵特性:凸函數的任何局部最小值都是全局最小值。
- 常見例子:線性迴歸(MSE 損失)、邏輯迴歸(交叉熵損失)、SVM(原始或對偶問題)。
- 優點:存在高效且保證收斂到全局最優解的算法。
#31
★★★★
非凸優化 (Non-convex Optimization)
優化類型
如果目標函數或可行域是非凸的,則為非凸優化問題。
- 關鍵特性:可能存在多個局部最小值和鞍點。優化算法不保證找到全局最優解。
- 常見例子:深度神經網路的訓練。
- 挑戰:優化過程更困難,結果可能依賴於初始值和算法選擇。
#32
★★
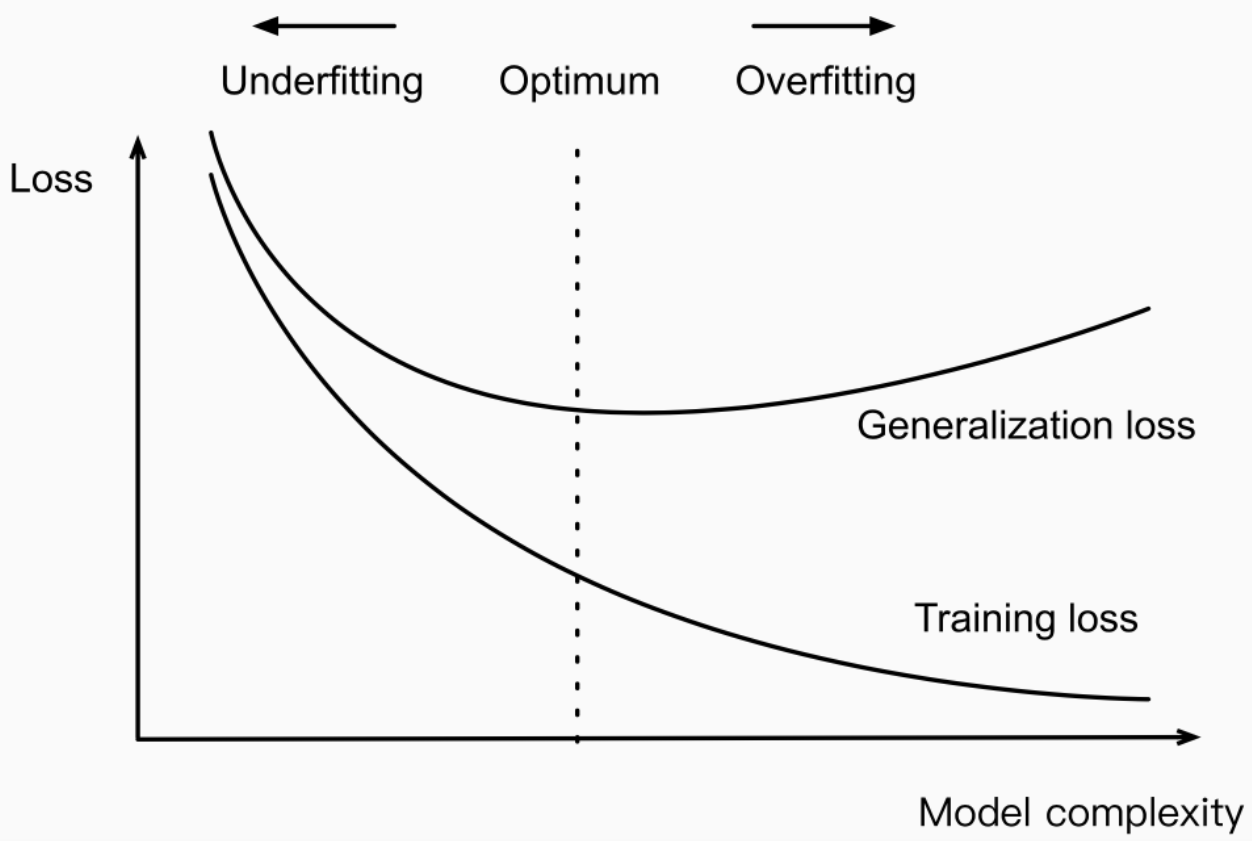
優化與泛化 (Generalization) 的關係
關係
優化的目標是最小化訓練集上的損失,但機器學習的最終目標是獲得良好的泛化能力(在未見數據上的表現)。過度優化訓練損失可能導致過擬合,損害泛化能力。需要平衡優化程度和泛化性能。
#33
★
替代損失 (Surrogate Loss)
概念
有時,我們真正關心的評估指標(如 0-1 損失)難以直接優化(不連續或不可微)。此時會選擇一個易於優化的替代損失函數(如 Hinge 損失、交叉熵損失)來近似原始目標。
#34
★★
梯度檢查 (Gradient Checking)
驗證方法
一種數值方法(通常使用有限差分)來近似梯度,用於驗證反向傳播算法計算出的解析梯度是否正確。主要用於代碼除錯,計算成本高,不應在實際訓練中使用。
#35
★
批次大小 (Batch Size) 的影響
超參數影響
- 較小批次: 梯度噪聲大,訓練不穩定,但可能幫助跳出局部最優;泛化性能有時更好。
- 較大批次: 梯度更準確,訓練穩定,收斂快(每次迭代),但可能收斂到較差的(尖銳的)最小值;計算資源需求高。
#36
★★
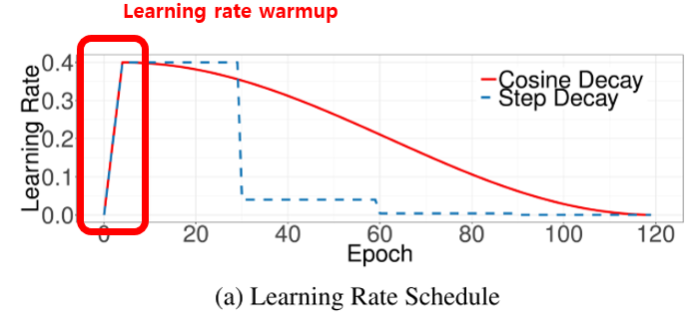
學習率預熱 (Learning Rate Warmup)
訓練技巧
在訓練初期使用一個非常小的學習率,然後逐漸增加到預設的初始學習率。有助於在訓練開始時穩定參數更新,特別是對於使用 Adam 等自適應優化器或大型模型。
#37
★
AdaDelta
自適應優化器
Adagrad 的另一種擴展,也試圖解決其學習率單調遞減問題。它不需要手動設定全局學習率。
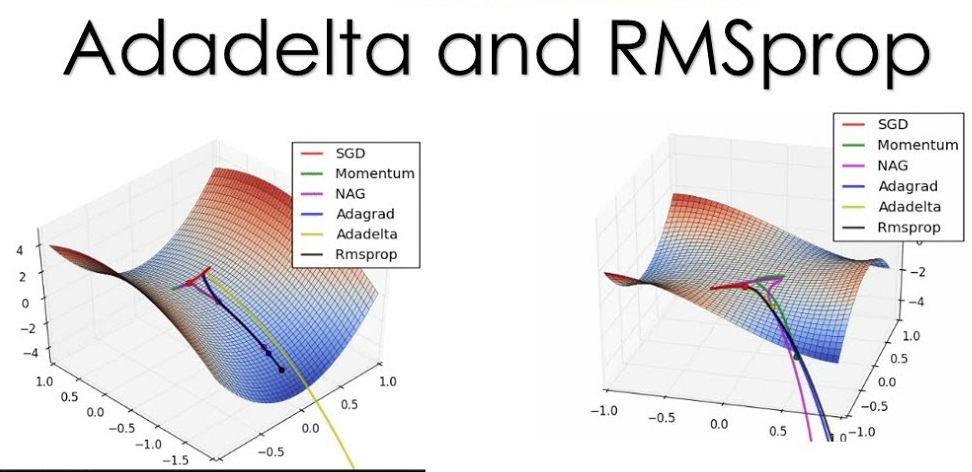
#38
★★
條件數 (Condition Number)
優化相關
衡量問題對輸入擾動的敏感性。在優化中,損失函數的 Hessian 矩陣的條件數會影響梯度下降的收斂速度。條件數過大(病態問題)會導致收斂緩慢。
#39
★★
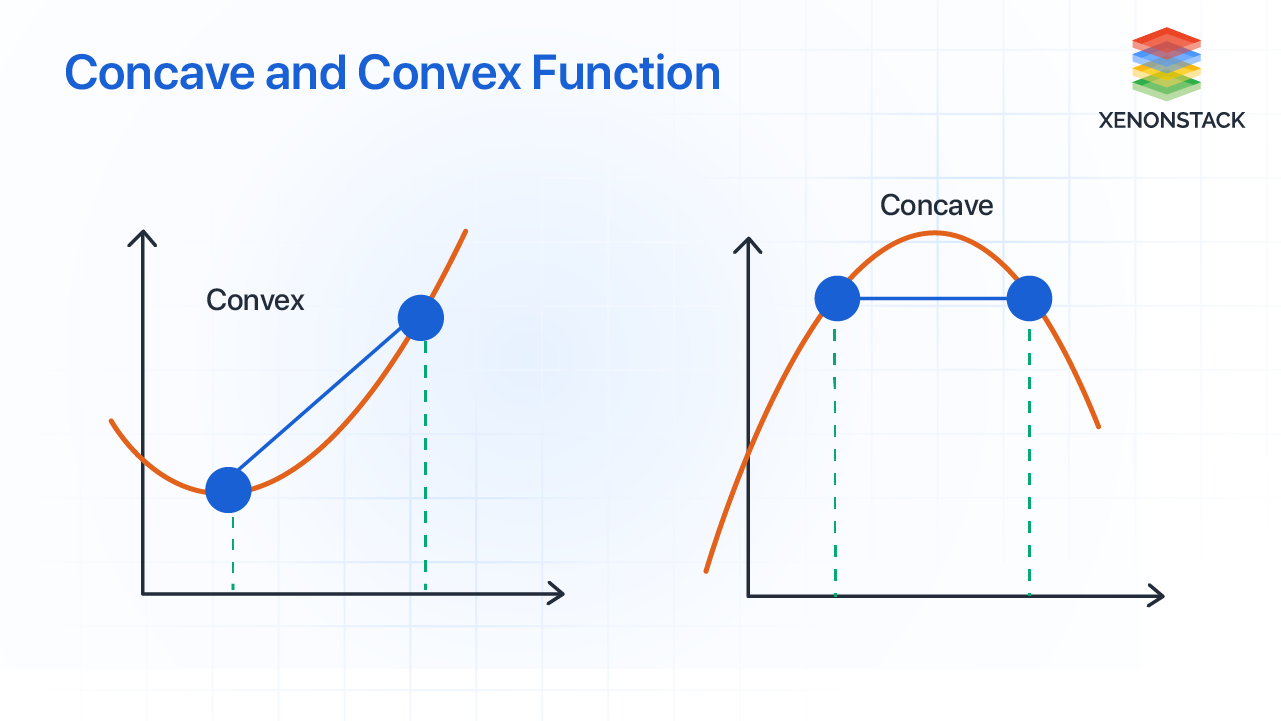
凸函數 (Convex Function) 的定義
數學定義
一個函數是凸函數,如果其定義域是凸集,並且對於定義域中任意兩點 x, y 和任意 0≤λ≤1,滿足 f(λx + (1-λ)y) ≤ λf(x) + (1-λ)f(y)。直觀上,函數圖形上任意兩點連線段都在函數圖形的上方(或重合)。
#41
★
無約束優化 vs. 約束優化 (Unconstrained Optimization vs. Constrained Optimization)
優化類型
無約束優化指在參數空間中沒有任何限制條件的優化問題,而約束優化則需要在滿足某些等式或不等式約束條件的情況下進行優化。機器學習中常見的梯度下降基本屬於無約束優化,但有時會加入正則化等軟約束。

#42
★
線上梯度下降 (Online Gradient Descent)
學習方式
SGD 的別稱,特別強調其處理數據流、進行增量學習的能力。

#43
★
優化過程的視覺化
輔助理解
繪製損失函數的等高線圖以及參數更新的軌跡,有助於直觀理解不同優化演算法和學習率的行為。
#44
★
AdamW
Adam 變體
對 Adam 算法中權重衰減(L2 正則化)的實現方式進行了修正,認為能獲得更好的泛化性能。
#45
★
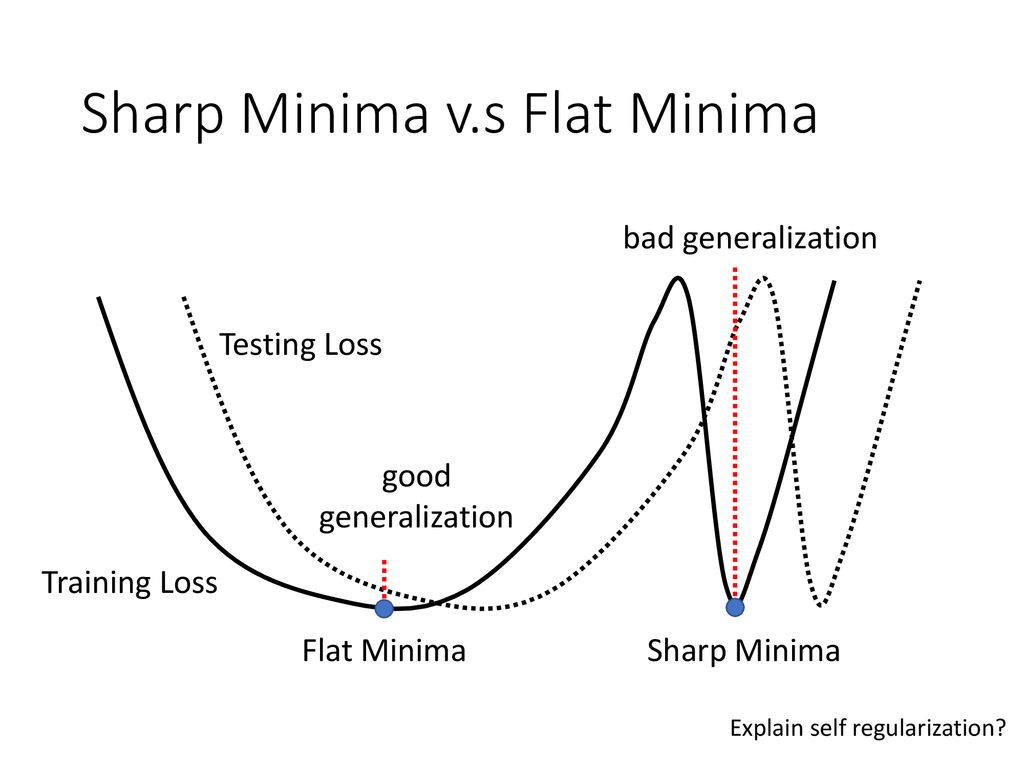
平坦最小值 (Flat Minima) vs. 尖銳最小值 (Sharp Minima)
優化區域特性
研究表明,優化算法收斂到的平坦最小值(周圍損失變化不大)通常比尖銳最小值(周圍損失變化劇烈)具有更好的泛化能力。較大的批次大小可能傾向於收斂到尖銳最小值。
#46
★
強凸性 (Strong Convexity)
數學性質
比凸性更強的條件,要求函數「足夠彎曲」。強凸函數保證有唯一的全局最小值,並且許多優化算法的收斂速度更快。
#47
★
最優解 (Optimal Solution)
術語
使得目標函數達到最小值(或最大值)的那組參數值。在非凸優化中,找到的可能是局部最優解。
#48
★
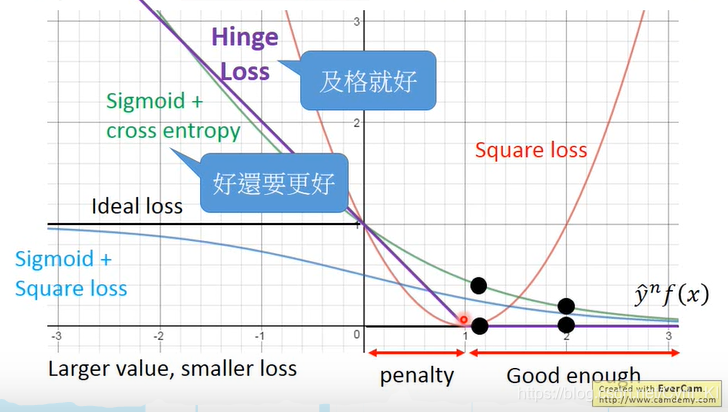
Hinge 損失
損失函數
常用於 SVM。其特點是對於分類正確且邊界足夠大的樣本,損失為零。
#49
★
次梯度 (Subgradient)
數學概念
對於不可微的凸函數(如包含 L1 正則化的目標函數),可以使用次梯度來代替梯度進行優化。
#50
★
停止準則 (Stopping Criteria)
迭代終止
決定迭代優化何時停止的條件,例如:達到最大迭代次數、目標函數值變化小於閾值、梯度大小小於閾值、驗證集性能不再提升(提早停止)。
#51
★
Nadam
Adam 變體
結合了 Adam 和 NAG (Nesterov Accelerated Gradient) 思想的優化器。
#52
★
隨機性的作用
優化影響
在優化過程中引入隨機性(如 SGD、Dropout、隨機初始化)有時有助於探索更廣泛的參數空間,避免陷入不良的局部解。
#53
★
線搜索 (Line Search)
優化技術
在梯度下降等方法中,除了確定下降方向(負梯度),還需要確定沿該方向移動的步長(學習率)。線搜索是一種尋找最優步長的策略,但計算成本較高,在大型 ML 中較少直接使用固定步長或衰減策略。
#54
★
參數空間 (Parameter Space)
概念
模型所有可能參數值構成的多維空間。優化的過程就是在這個空間中搜索使目標函數最優的點。
#55
★
損失函數的選擇與優化難度
關係
不同的損失函數具有不同的形狀(如是否凸),這會影響優化的難易程度和所選優化算法的收斂性。
#56
★
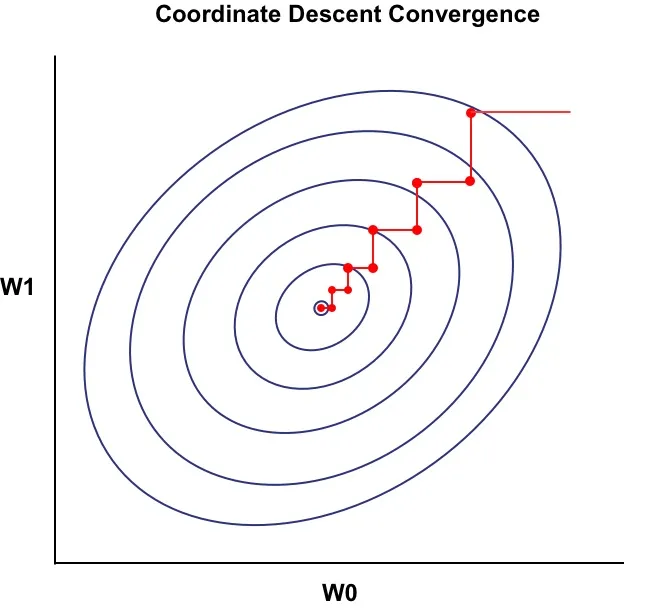
坐標下降法 (Coordinate Descent)
優化方法
一種優化方法,每次迭代只沿著一個坐標軸(參數)的方向進行優化,固定其他參數。適用於某些特定問題。
#57
★
學習曲線的平滑化
視覺化技巧
由於 SGD 或 Mini-batch 導致的噪聲,原始損失曲線可能會有很大波動。通常會使用移動平均等方法對損失曲線進行平滑化處理,以便更清晰地觀察趨勢。
#58
★
優化器超參數調整
調優細節
除了學習率,進階優化器(如 Adam)本身也有一些超參數(如 β₁, β₂, ε)可能需要調整,儘管通常使用預設值即可。
#59
★
病態曲率 (Ill-conditioned Curvature)
優化挑戰
指損失函數在不同方向上的曲率(二階導數)差異很大,形成狹長的「峽谷」。這會導致梯度下降在峽谷壁之間來回震盪,收斂緩慢。二階方法或自適應方法有助於處理此問題。
#60
★
拉格朗日乘子法 (Lagrange Multipliers)
約束優化
一種用於求解帶有等式約束的優化問題的數學方法。
沒有找到符合條件的重點。
↑