iPAS AI應用規劃師考試重點整理 - L23102 線性代數在機器學習中的應用

#1

★★★★★

向量 (Vector) - 機器學習中的基礎

核心概念

向量是有序的數字列表，在機器學習中極為重要。常用來表示：

一個數據樣本的特徵 (Features)。
模型中的參數（例如，線性模型的權重、神經網路的偏置）。
文字的嵌入表示 (Word Embeddings)。

理解向量的表示和基本運算（加法、純量乘法、點積）是基礎。

#2

★★★★★

矩陣 (Matrix) - 數據與參數的集合

核心概念

矩陣是二維的數字陣列（由行和列組成）。在機器學習中常用來：

表示整個資料集（列代表樣本，欄代表特徵）。
表示神經網路某一層的權重。
表示變換操作（如旋轉、縮放）。
表示協方差矩陣、相似度矩陣等。

矩陣運算是許多 ML 演算法的核心。

#3

★★★★

張量 (Tensor) - 多維數據表示

核心概念

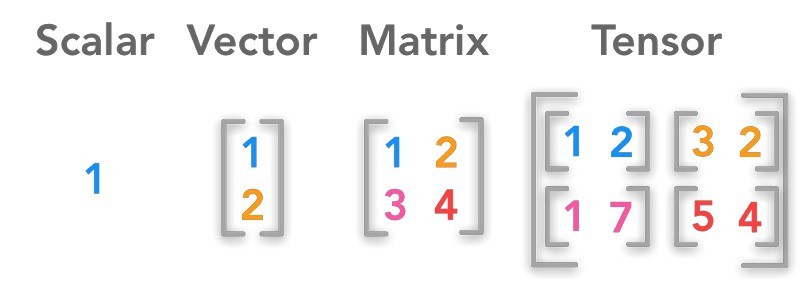
張量是向量和矩陣向更高維度的推廣。

0 階張量：純量 (Scalar)。
1 階張量：向量 (Vector)。
2 階張量：矩陣 (Matrix)。
3 階及以上張量：多維陣列。

在深度學習中，張量是基本數據結構，用於表示輸入數據（如彩色圖像寬x高x通道）、模型參數、中間計算結果等。

#4

★★★

矩陣的轉置 (Transpose)

基本操作

矩陣的轉置是指將其行和列互換。如果 A 是一個 m×n 的矩陣，其轉置 Aᵀ 是一個 n×m 的矩陣，其中 (Aᵀ)ᵢⱼ = Aⱼᵢ。轉置在許多 ML 公式推導和計算中很常見（例如，最小二乘法的正規方程）。

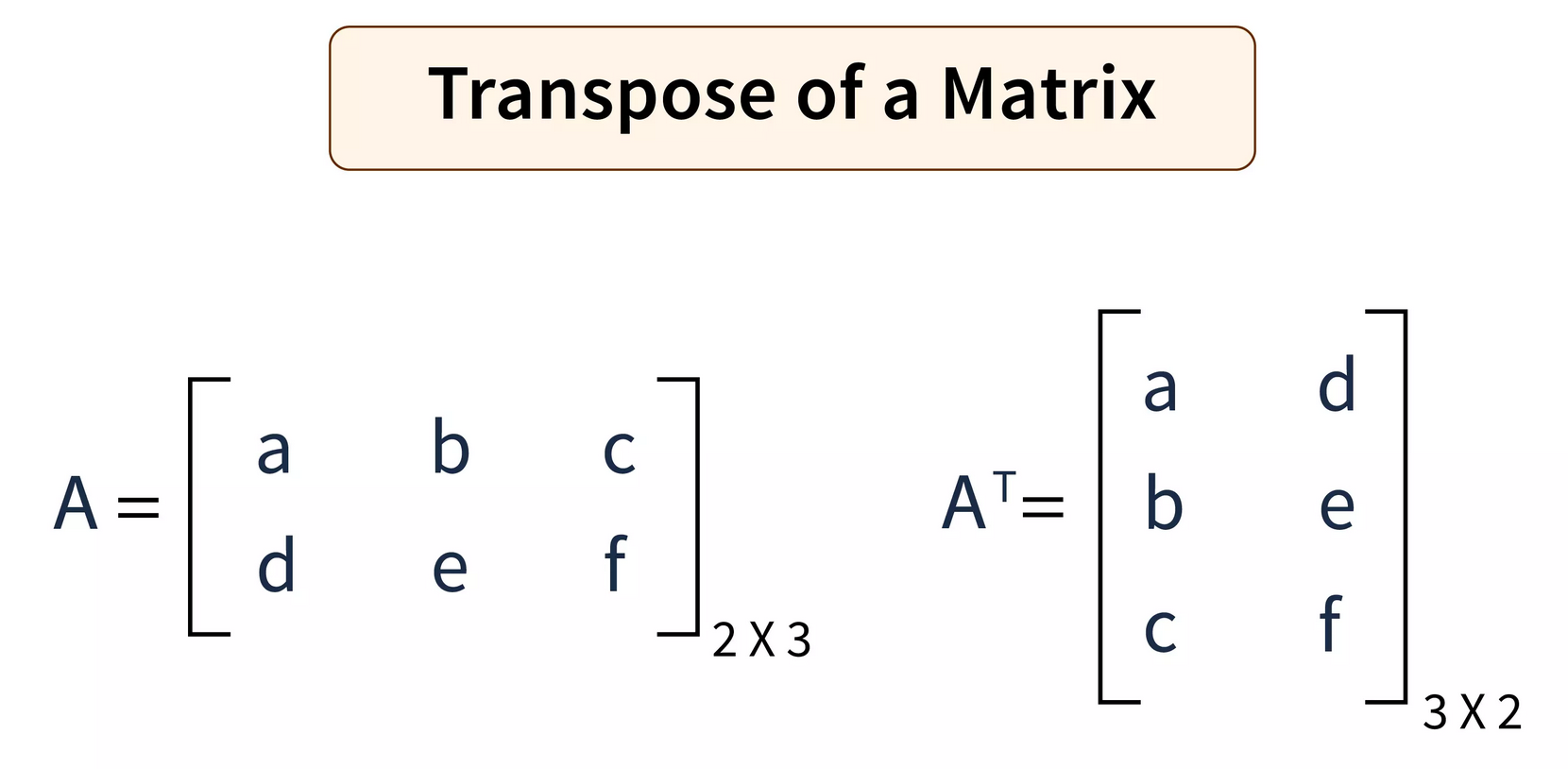
#5

★★★

單位矩陣 (Identity Matrix) 與逆矩陣 (Inverse Matrix)

特殊矩陣

單位矩陣 (I): 主對角線元素為 1，其餘為 0 的方陣。任何矩陣乘以單位矩陣等於其自身 (AI = IA = A)。

逆矩陣 (A⁻¹): 對於一個方陣 A，如果存在一個矩陣 A⁻¹ 使得 AA⁻¹ = A⁻¹A = I，則稱 A⁻¹ 為 A 的逆矩陣。只有非奇異方陣（行列式不為零）才有逆矩陣。逆矩陣用於求解線性方程組（例如，線性迴歸的正規方程）。

#6

★★★★★

使用向量表示數據樣本

數據表示

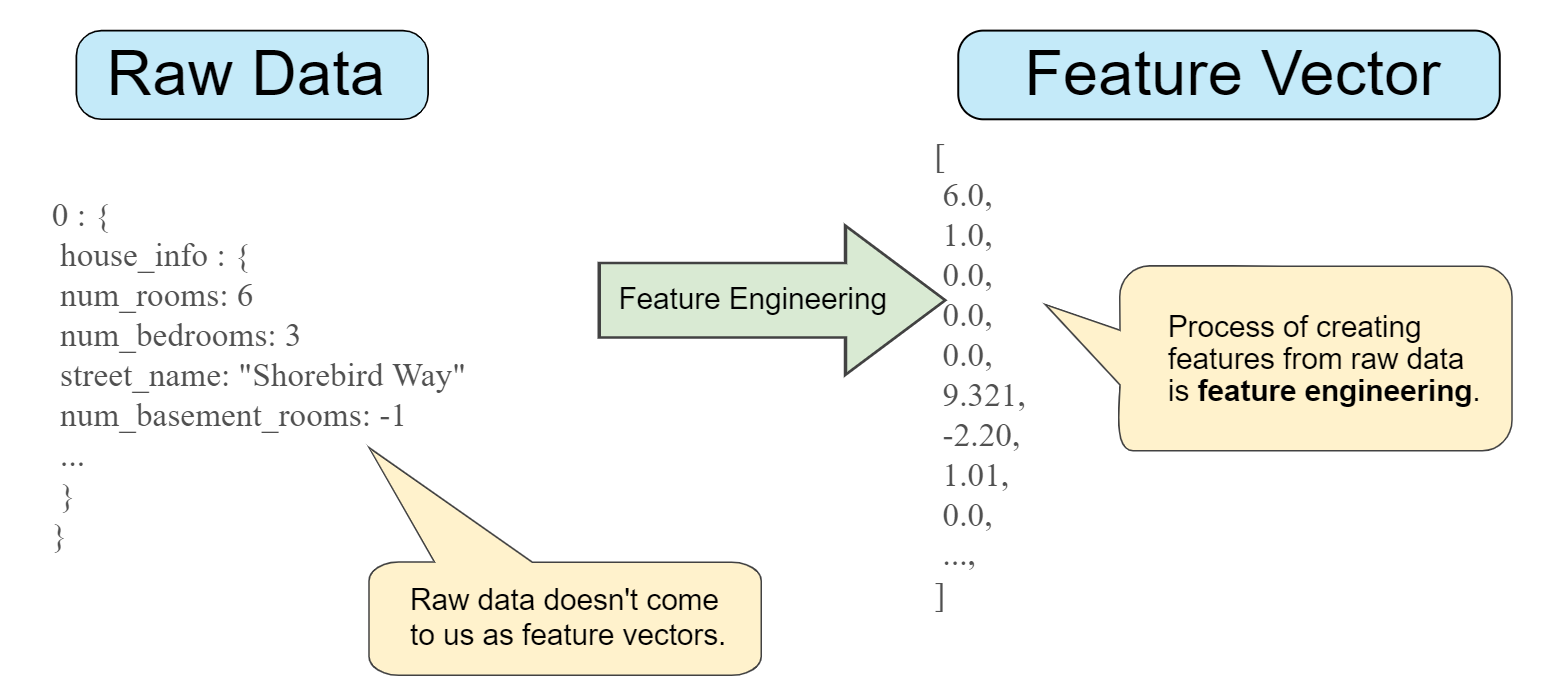
在機器學習中，通常將每個數據樣本表示為一個特徵向量 (Feature Vector)。向量的每個元素對應一個特徵的值。例如，一個包含房屋大小、房間數、屋齡的樣本可以表示為向量 [大小, 房間數, 屋齡]。這種表示方式使得數據可以用線性代數工具進行處理。

#7

★★★★★

使用矩陣表示資料集

資料表示

一個包含多個樣本的資料集通常被表示為一個資料矩陣（或設計矩陣, Design Matrix），通常記為 X。

矩陣的每一列通常代表一個資料樣本（一個特徵向量）。
矩陣的每一行通常代表一個特定的特徵。

如果資料集有 m 個樣本和 n 個特徵，則資料矩陣 X 的維度為 m×n。

#8

★★★★

使用向量/矩陣表示模型參數

模型表示

許多機器學習模型的參數也可以用向量或矩陣表示：

線性迴歸：權重係數可以表示為一個權重向量 w。
神經網路：每一層的權重通常表示為一個權重矩陣 W，偏置表示為一個偏置向量 b。

這種表示使得模型計算可以用高效的線性代數運算來實現。

#9

★★★★

使用張量表示高維數據 (圖像, 影像)

數據表示

對於維度超過二維的數據，需要使用張量來表示：

灰度圖像：通常表示為 2 階張量 (矩陣) (寬度 × 高度)。
彩色圖像：通常表示為 3 階張量 (寬度 × 高度 × 色彩通道數)。
影像 (影片)：通常表示為 4 階張量 (幀數 × 寬度 × 高度 × 色彩通道數)。
批次數據：在深度學習訓練中，通常會將一批樣本組合成更高階的張量（例如，一批彩色圖像為 4 階張量：批次大小 × 寬度 × 高度 × 通道數）。

#10

★★★★★

向量點積 (Dot Product) / 內積 (Inner Product)

核心運算

兩個維度相同的向量 u 和 v 的點積（記為 u ⋅ v 或 uᵀv）是將它們對應元素相乘後求和的純量結果。
u ⋅ v = Σ uᵢvᵢ
點積在機器學習中非常重要：

計算加權和（如神經元的輸入）。
計算向量的長度（範數）的平方 (v ⋅ v = ||v||²)。
計算兩個向量之間的投影或相似度（透過餘弦相似度）。

#11

★★★★★

矩陣乘法 (Matrix Multiplication)

核心運算

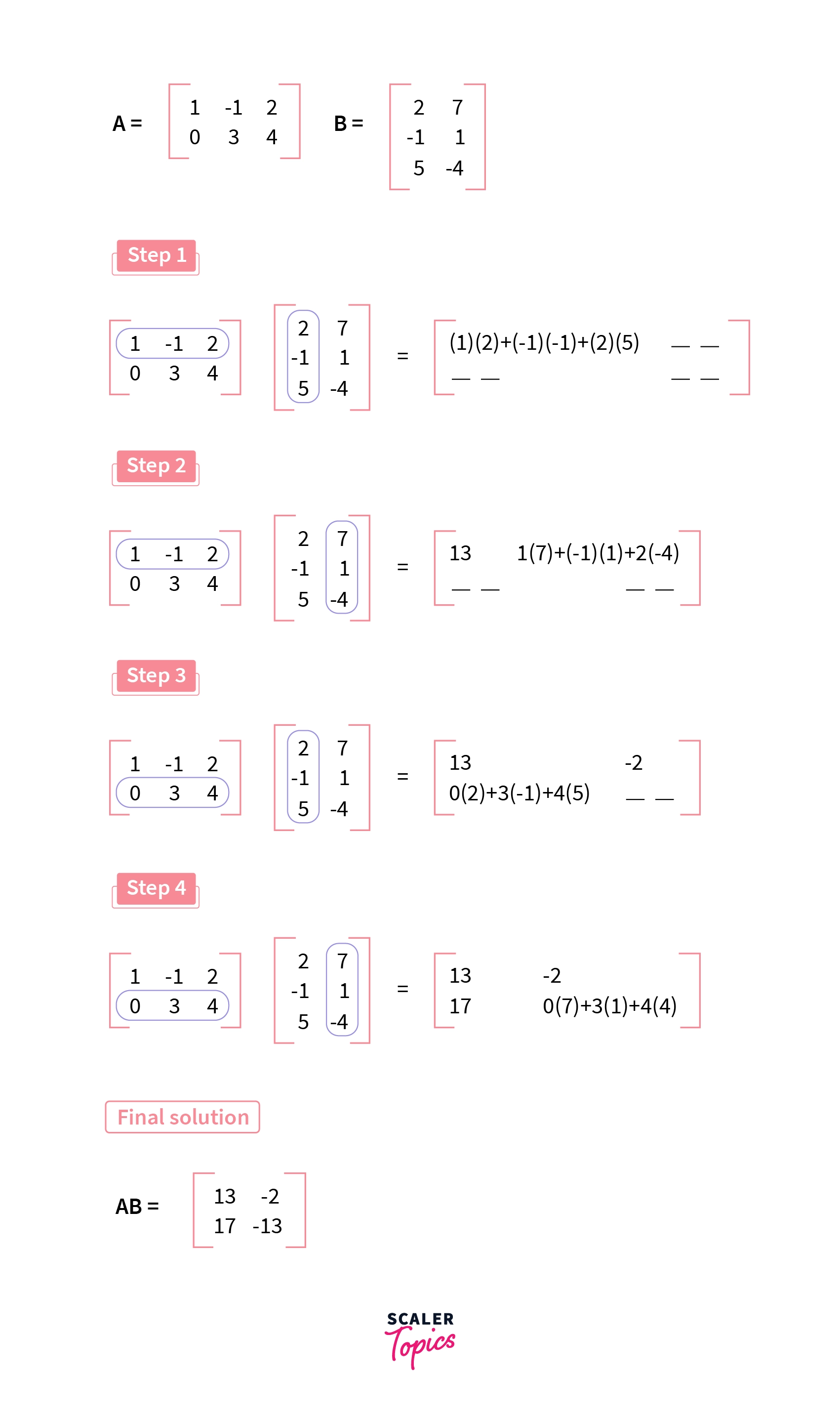
矩陣乘法是最核心的線性代數運算之一，在機器學習（尤其是深度學習）中無處不在。

如果 A 是 m×n 矩陣，B 是 n×p 矩陣，則它們的乘積 C = AB 是一個 m×p 矩陣，其中 Cᵢⱼ 是 A 的第 i 行與 B 的第 j 列的點積。
矩陣乘法不滿足交換律 (AB ≠ BA)。
應用：線性變換、神經網路層的計算（權重矩陣乘以輸入向量/矩陣）、數據轉換等。

#12

★★★

矩陣-向量乘法 (Matrix-Vector Multiplication)

核心運算

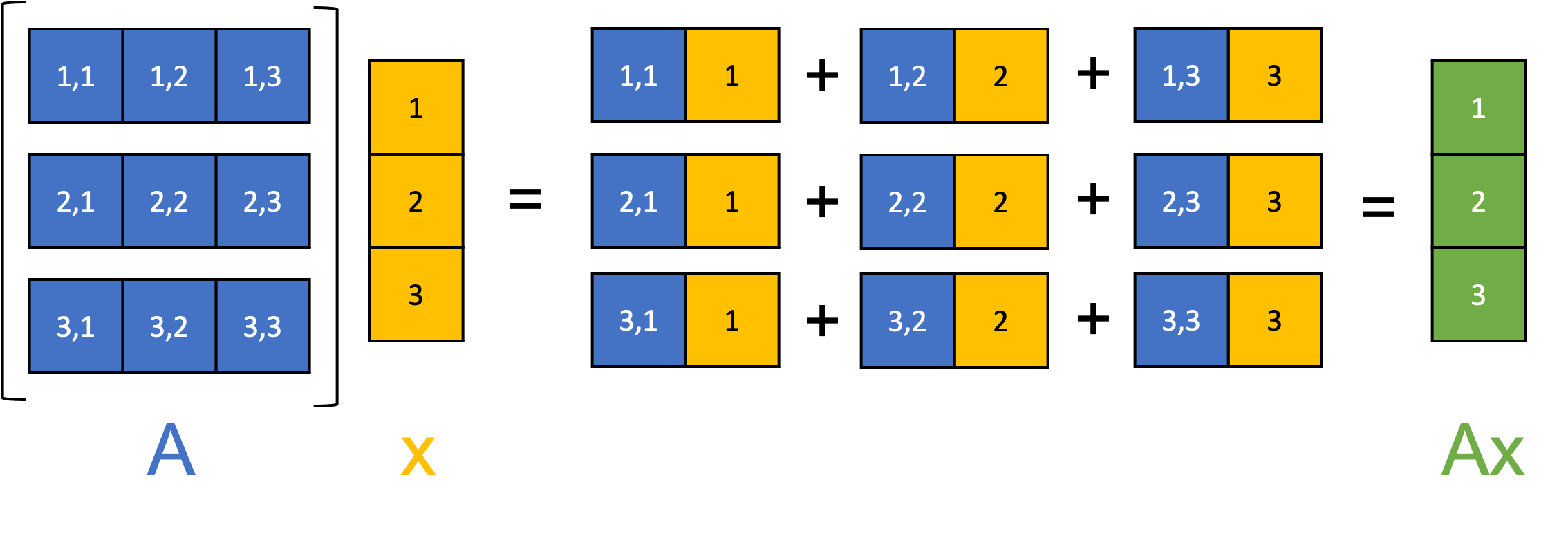
矩陣乘以向量是矩陣乘法的特例。如果 A 是 m×n 矩陣，v 是 n×1 向量（列向量），則結果 Av 是一個 m×1 向量。結果向量的第 i 個元素是矩陣 A 的第 i 行與向量 v 的點積。
常用於：計算線性模型的預測值 (y = Xw)，計算神經網路層的輸出 (z = Wx + b)。

#13

★★

逐元素運算 (Element-wise Operations)

常見運算

對兩個相同形狀的向量或矩陣（或張量）的對應元素進行運算。例如：

逐元素加法/減法。
逐元素乘法（哈達瑪積, Hadamard Product），不同於矩陣乘法。
逐元素應用函數（如激活函數 ReLU, Sigmoid）。

在深度學習框架中非常常見。

#14

★★★★

線性方程組 (System of Linear Equations) 的矩陣表示

表示方法

一個包含 m 個方程和 n 個未知數的線性方程組可以緊湊地表示為矩陣形式：
Ax = b
其中：

A 是 m×n 的係數矩陣。
x 是 n×1 的未知數向量。
b 是 m×1 的常數向量。

許多機器學習問題最終歸結為求解這類方程組。

#15

★★★★

線性迴歸 (Linear Regression) 的正規方程解 (Normal Equation)

應用實例 (參考樣題 Q9)

對於線性迴歸問題 y ≈ Xw，最小化均方誤差 (MSE) 的閉式解（解析解）可以透過正規方程給出：
w = (XᵀX)⁻¹Xᵀy
這個解直接使用了矩陣轉置、矩陣乘法和矩陣求逆等線性代數運算。它提供了一種無需迭代優化（如梯度下降）即可求解線性迴歸的方法（但要求 XᵀX 可逆且計算成本在特徵數 n 很大時較高）。

#16

★★★

矩陣的秩 (Rank)

矩陣性質

矩陣的秩是指其線性獨立的行（或列）的最大數量。

滿秩 (Full Rank): 方陣的秩等於其維度。滿秩方陣是可逆的。

秩虧 (Rank Deficient): 秩小於行數或列數的最小值。

矩陣的秩與線性方程組解的存在性和唯一性有關。例如，在正規方程中，如果 XᵀX 秩虧（通常由特徵間共線性引起），則其不可逆。

#17

★★★★★

特徵值 (Eigenvalue) 與特徵向量 (Eigenvector)

核心概念

對於一個方陣 A，如果存在一個非零向量 v 和一個純量 λ，使得 Av = λv，則 λ 稱為矩陣 A 的一個特徵值，v 稱為對應於 λ 的特徵向量。
直觀意義：特徵向量 v 是指被矩陣 A 變換後方向不變（只進行縮放）的向量，而特徵值 λ 就是這個縮放的比例。
特徵值和特徵向量在許多機器學習演算法中扮演重要角色，尤其是在降維（如 PCA）和矩陣分解中。

#18

★★★★★

主成分分析 (PCA, Principal Component Analysis) 的線性代數基礎

應用實例 (參考樣題 Q9 選項)

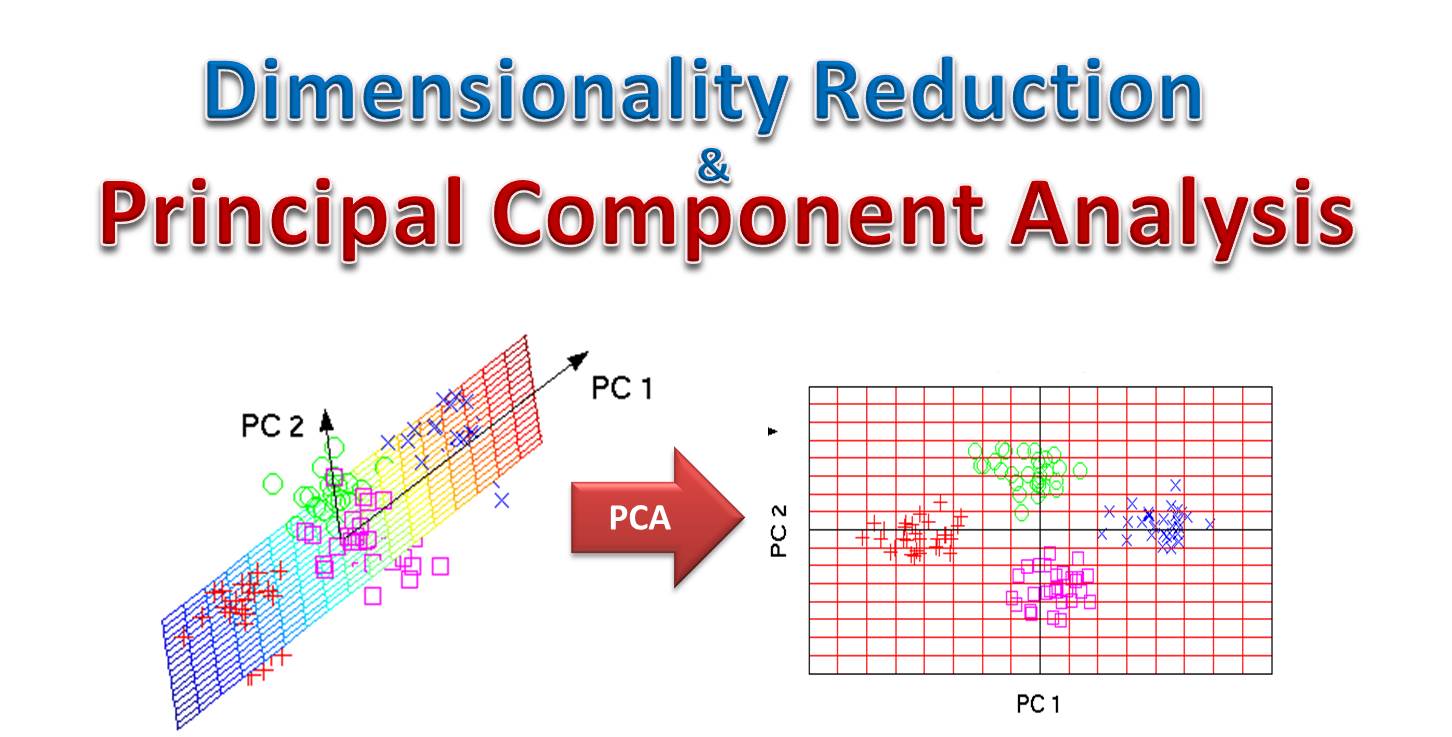
PCA 是一種常用的無監督降維方法，其核心是尋找數據變異最大的方向（主成分）。
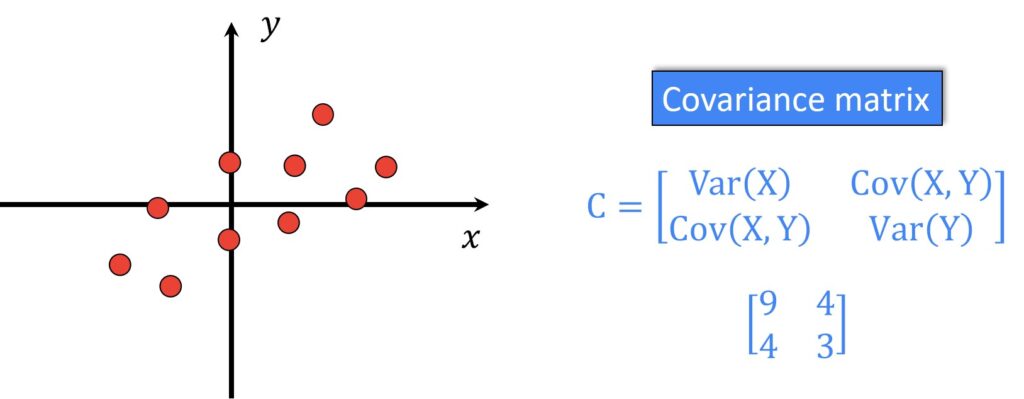
數學上，主成分對應於數據協方差矩陣 (Covariance Matrix) 的特徵向量，而特徵值則表示了每個主成分方向上的數據變異量大小。
通過選擇最大特徵值對應的特徵向量（主成分），可以將數據投影到保留最多資訊的低維空間。

#19

★★★

奇異值分解 (SVD, Singular Value Decomposition)

矩陣分解

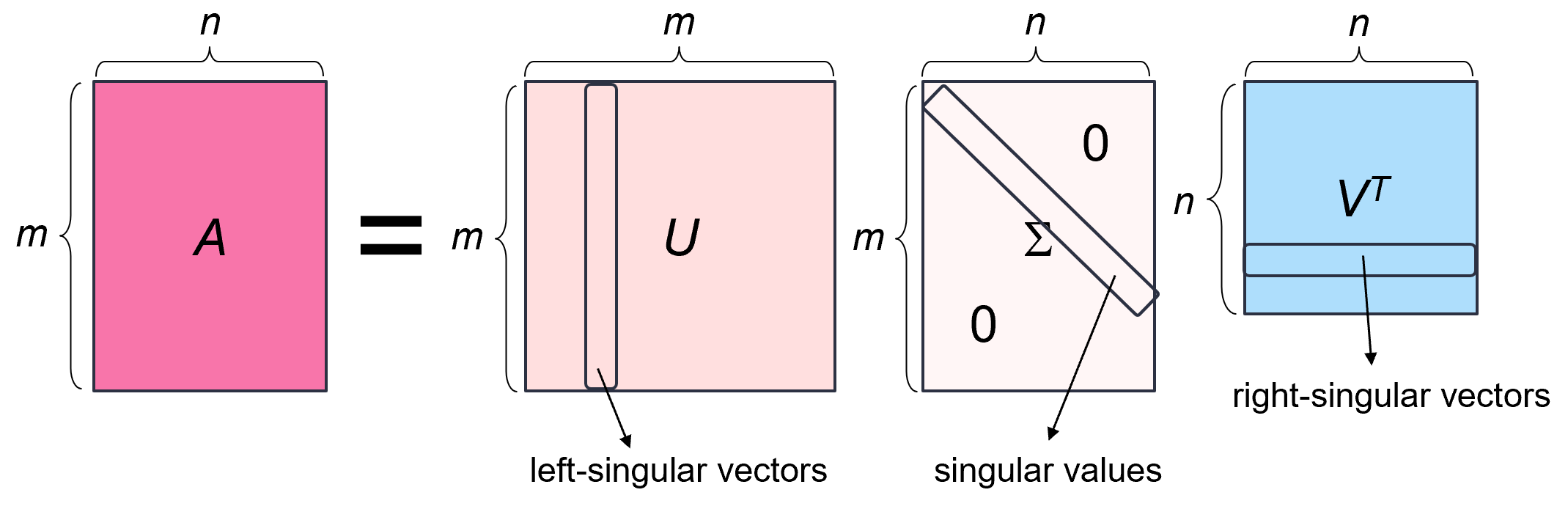
SVD 是一種重要的矩陣分解技術，可以將任意 m×n 矩陣 A 分解為三個矩陣的乘積：A = UΣVᵀ。

U 是 m×m 的正交矩陣 (其列為左奇異向量)。
Σ 是 m×n 的對角矩陣 (對角線元素為奇異值，非負且遞減排序)。
Vᵀ 是 n×n 的正交矩陣 V 的轉置 (V 的列為右奇異向量)。

SVD 在降維（類似 PCA）、推薦系統（矩陣填充）、自然語言處理（LSA）等領域有廣泛應用。

#20

★★

特徵分解 (Eigendecomposition)

矩陣分解

對於某些方陣（特別是對稱矩陣），可以將其分解為 A = PDP⁻¹ 的形式，其中 P 是由 A 的特徵向量組成的矩陣，D 是由對應特徵值組成的對角矩陣。特徵分解揭示了矩陣的內在結構和變換特性。PCA 可以看作是對協方差矩陣進行特徵分解。

#21

★★★★

向量範數 (Vector Norm) - 衡量向量大小

核心概念

向量範數是用於衡量向量「長度」或「大小」的函數。常見的範數包括：

L1 範數 (Manhattan Norm): ||v||₁ = Σ |vᵢ|，向量元素絕對值之和。
L2 範數 (Euclidean Norm): ||v||₂ = √(Σ vᵢ²)，向量的歐幾里得長度。
L∞ 範數 (Max Norm): ||v||∞ = max |vᵢ|，向量元素絕對值的最大值。

範數在正則化、距離計算和誤差衡量中非常重要。

#22

★★★★★

L1 與 L2 範數在正則化中的應用 (參考樣題 Q3)

應用實例

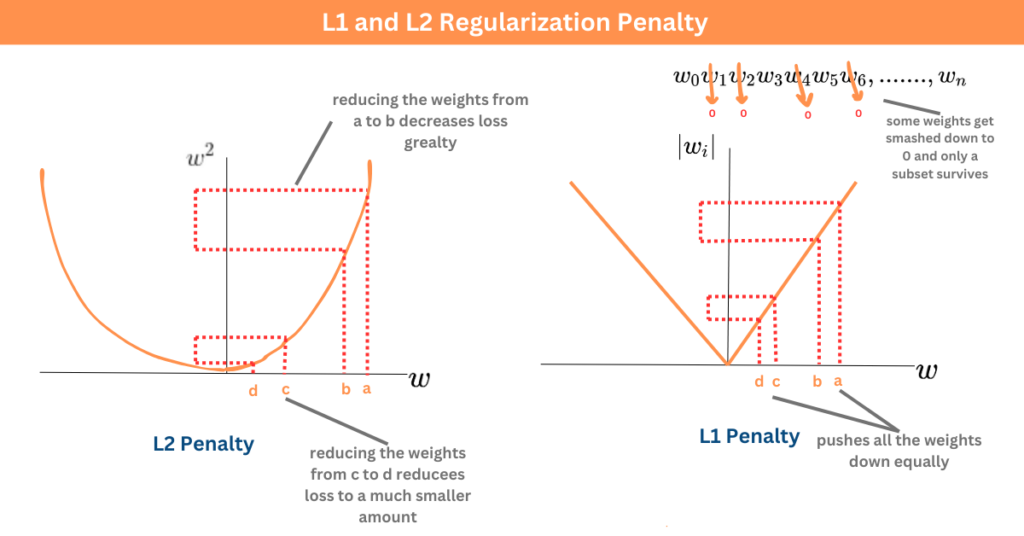
在機器學習模型（如線性迴歸、神經網路）的損失函數中加入參數（權重）向量的範數作為懲罰項，以防止過擬合：

L1 正則化 (Lasso): 使用權重向量的 L1 範數。傾向於產生稀疏解（部分權重為零），實現特徵選擇。
L2 正則化 (Ridge/Weight Decay): 使用權重向量的 L2 範數的平方。傾向於使所有權重都變小，提高模型穩定性。

樣題 Q3 確認正則化用於降低過擬合。

#23

★★★★

歐幾里得距離 (Euclidean Distance)

距離度量

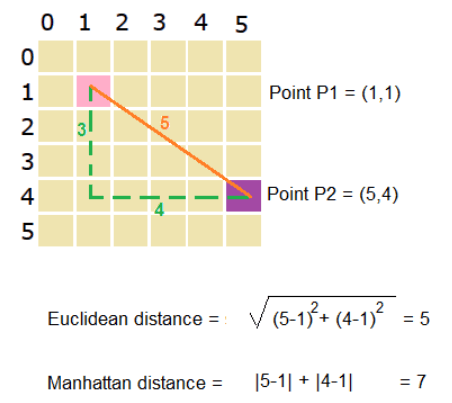
衡量兩個向量（數據點）在空間中直線距離的最常用方法。計算公式為兩向量差向量的 L2 範數：
d(u, v) = ||u - v||₂ = √(Σ (uᵢ - vᵢ)²)
廣泛應用於KNN、K-Means 等基於距離的演算法。

#24

★★★

餘弦相似度 (Cosine Similarity)

相似度度量

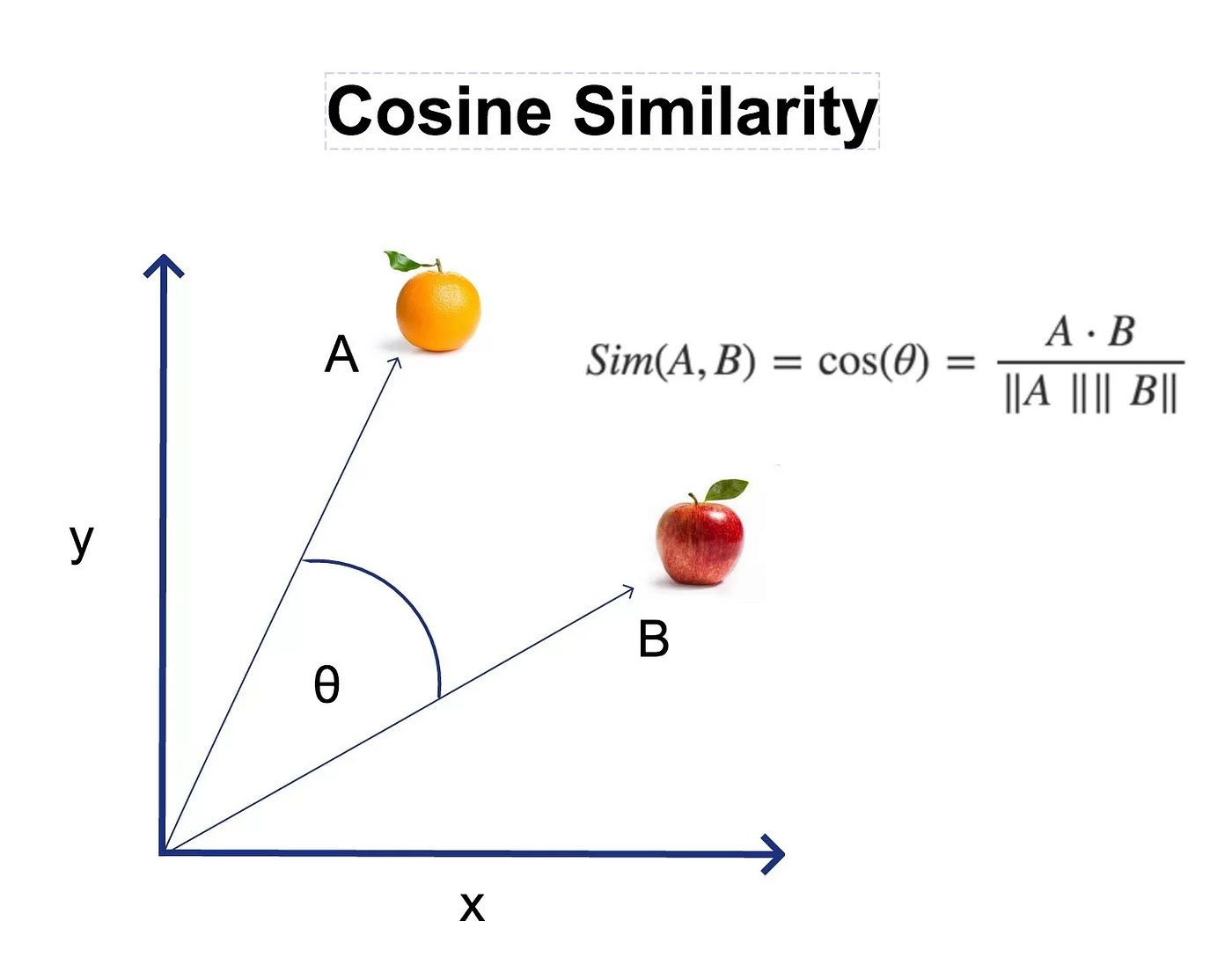
衡量兩個非零向量之間方向的相似性，而不考慮它們的大小（長度）。計算公式為兩向量點積除以它們 L2 範數的乘積：
similarity(u, v) = (u ⋅ v) / (||u||₂ ||v||₂)
值域為 [-1, 1]。值越接近 1 表示方向越相似。常用於文本分析（比較文檔向量）、推薦系統等。

#25

★★★★★

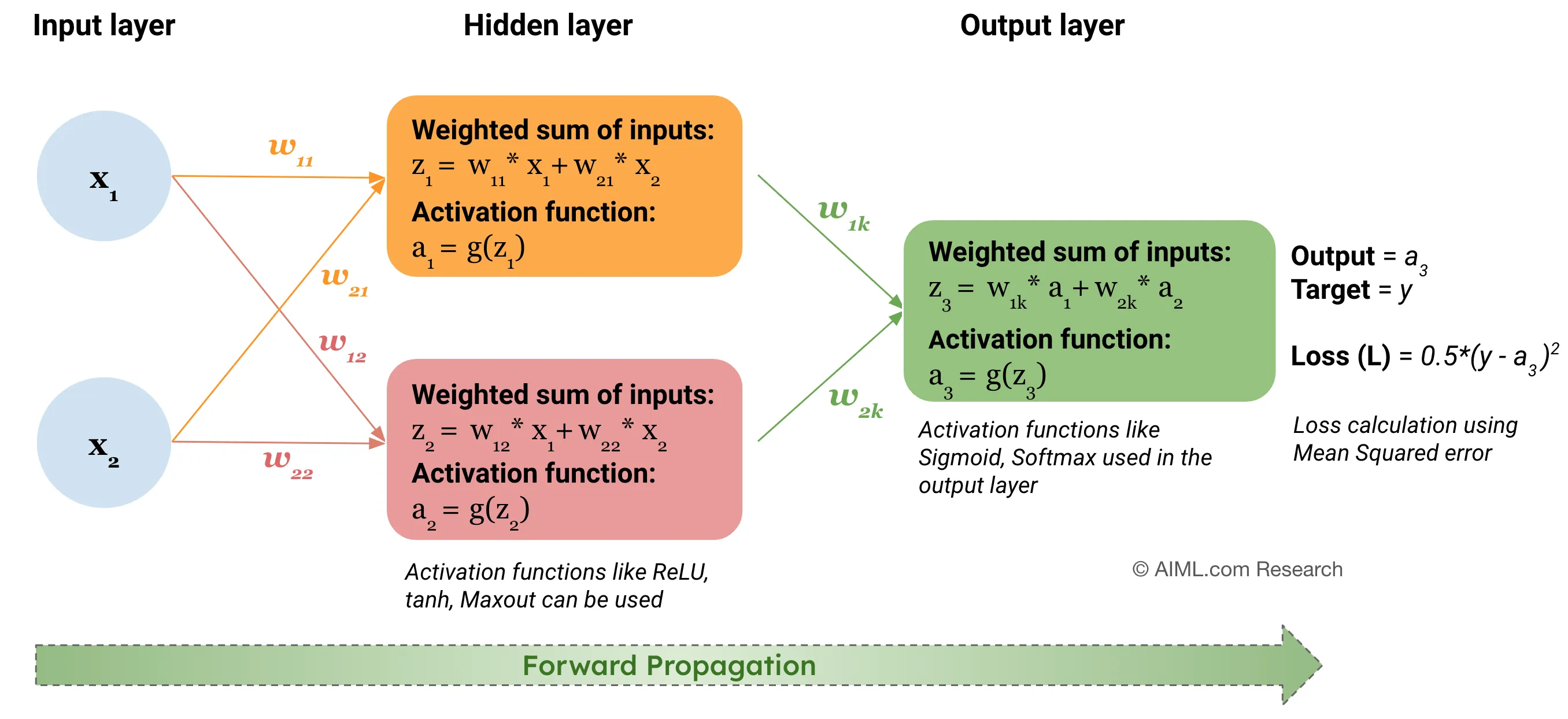
神經網路中的前向傳播 (Forward Propagation)

核心計算

指資訊從輸入層經過隱藏層逐層向前計算，最終到達輸出層產生預測值的過程。每層的計算主要涉及矩陣乘法（輸入乘以權重矩陣）和向量加法（加上偏置向量），然後通過激活函數。

#26

★★★★★

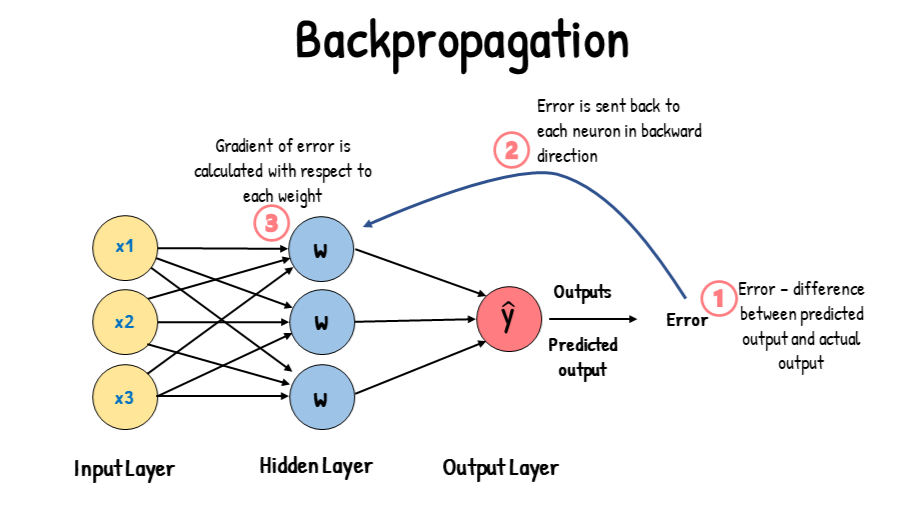
神經網路中的反向傳播 (Backpropagation)

核心訓練算法

反向傳播是計算損失函數相對於網路參數（權重和偏置）梯度的有效算法。它利用微積分的鏈式法則，從輸出層開始，逐層向後計算梯度。計算出的梯度用於梯度下降更新參數。整個過程依賴於線性代數運算（特別是矩陣和向量的導數）。

#27

★★★★

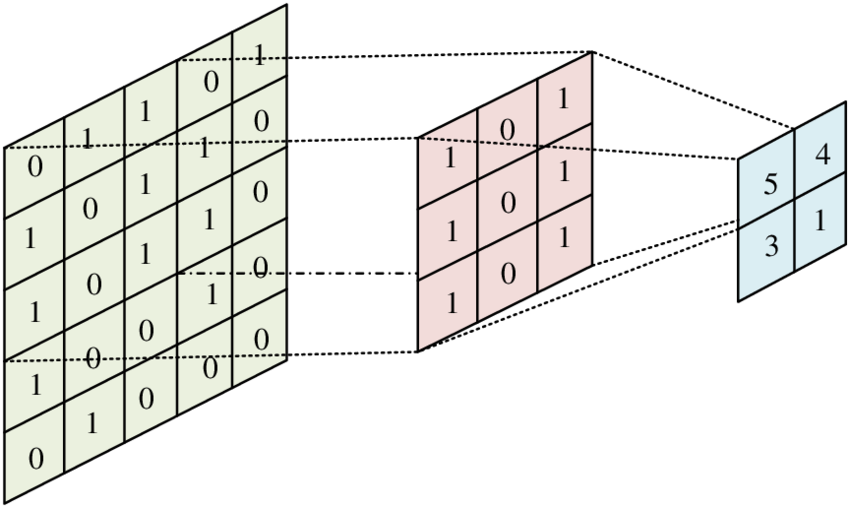
卷積 (Convolution) 操作的數學本質

CNN 核心

在CNN中，卷積操作本質上是將一個小的卷積核（矩陣）在輸入圖像（或特徵圖，矩陣/張量）上滑動，在每個位置計算卷積核與對應輸入區域的逐元素乘積之和（類似點積）。這可以看作是一種特殊的線性變換，利用線性代數進行高效計算。

#28

★★★

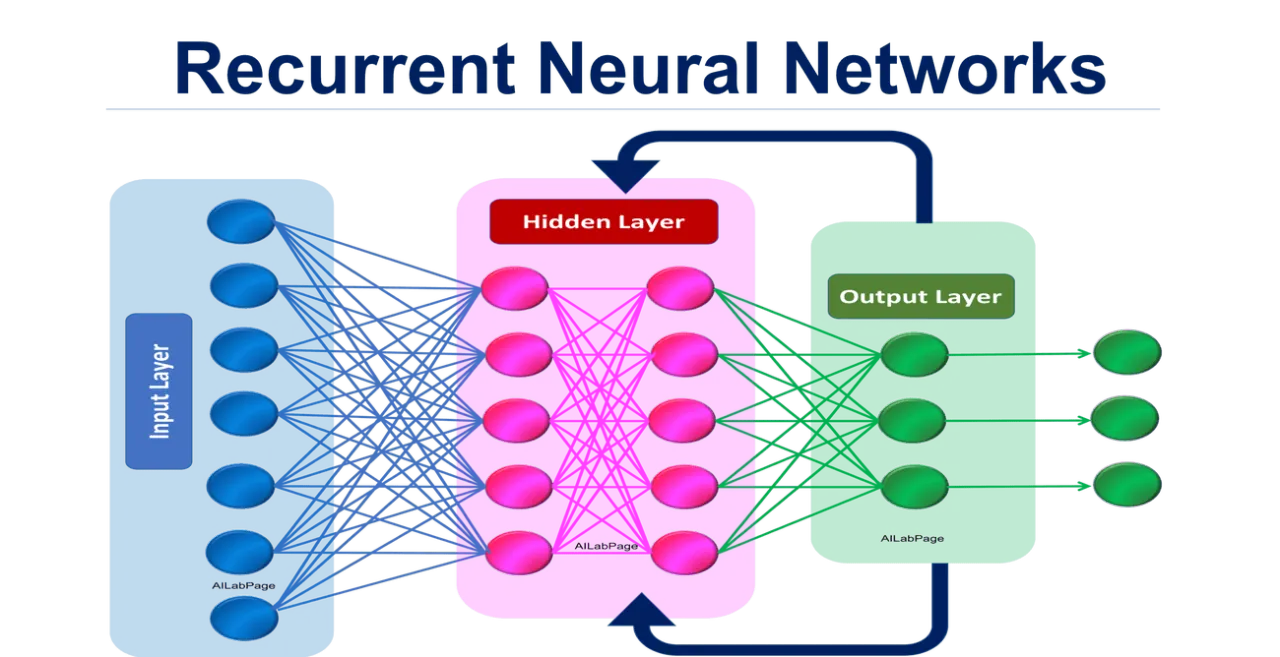
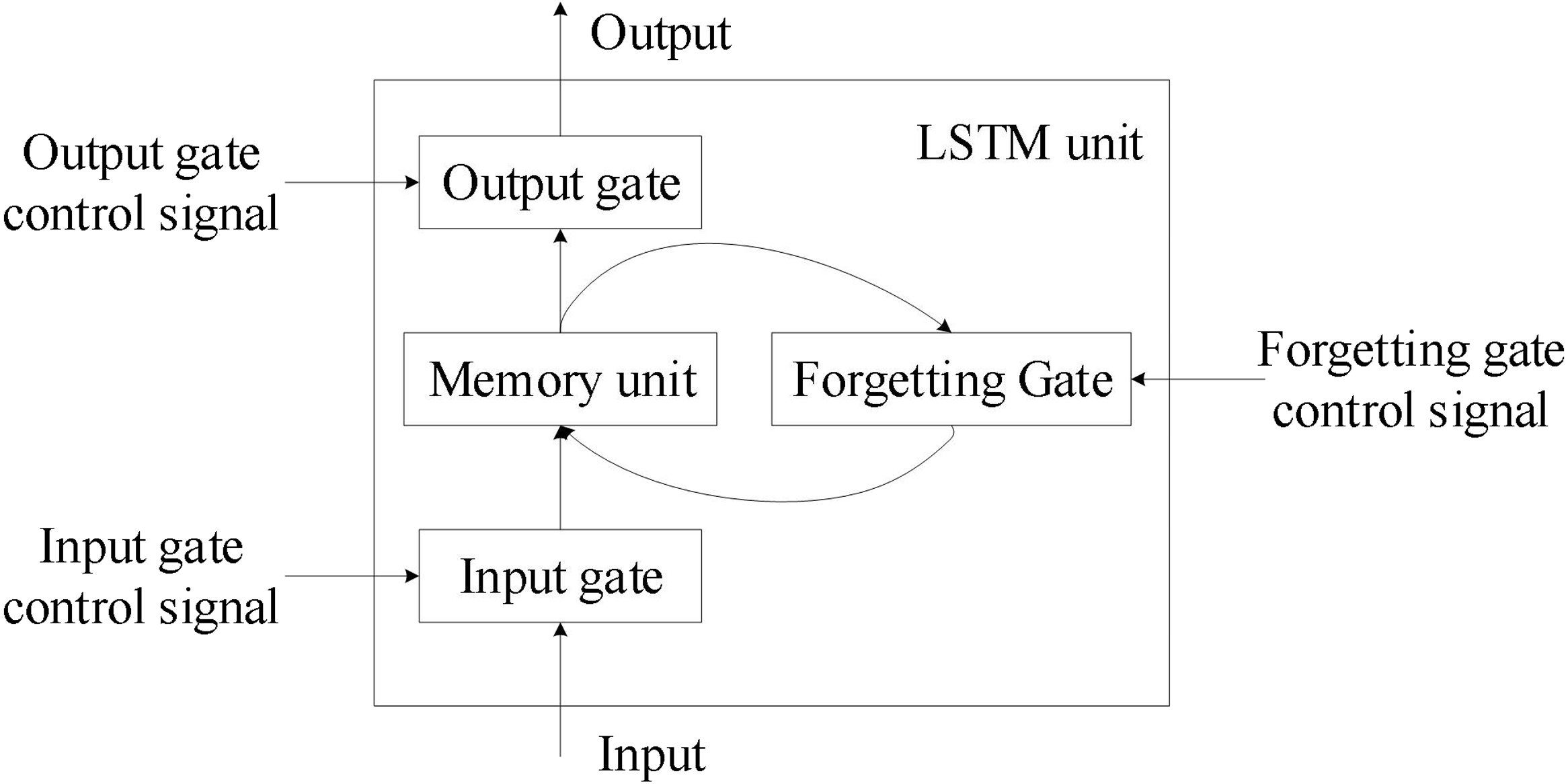
RNN/LSTM 中的矩陣運算

序列模型計算

在 RNN 及其變體 LSTM/GRU 中，每個時間步的計算都涉及將當前輸入和前一時間步的隱藏狀態透過權重矩陣進行線性變換，然後通過激活函數。門控機制（如遺忘門、輸入門）的計算也依賴於矩陣乘法和向量運算。

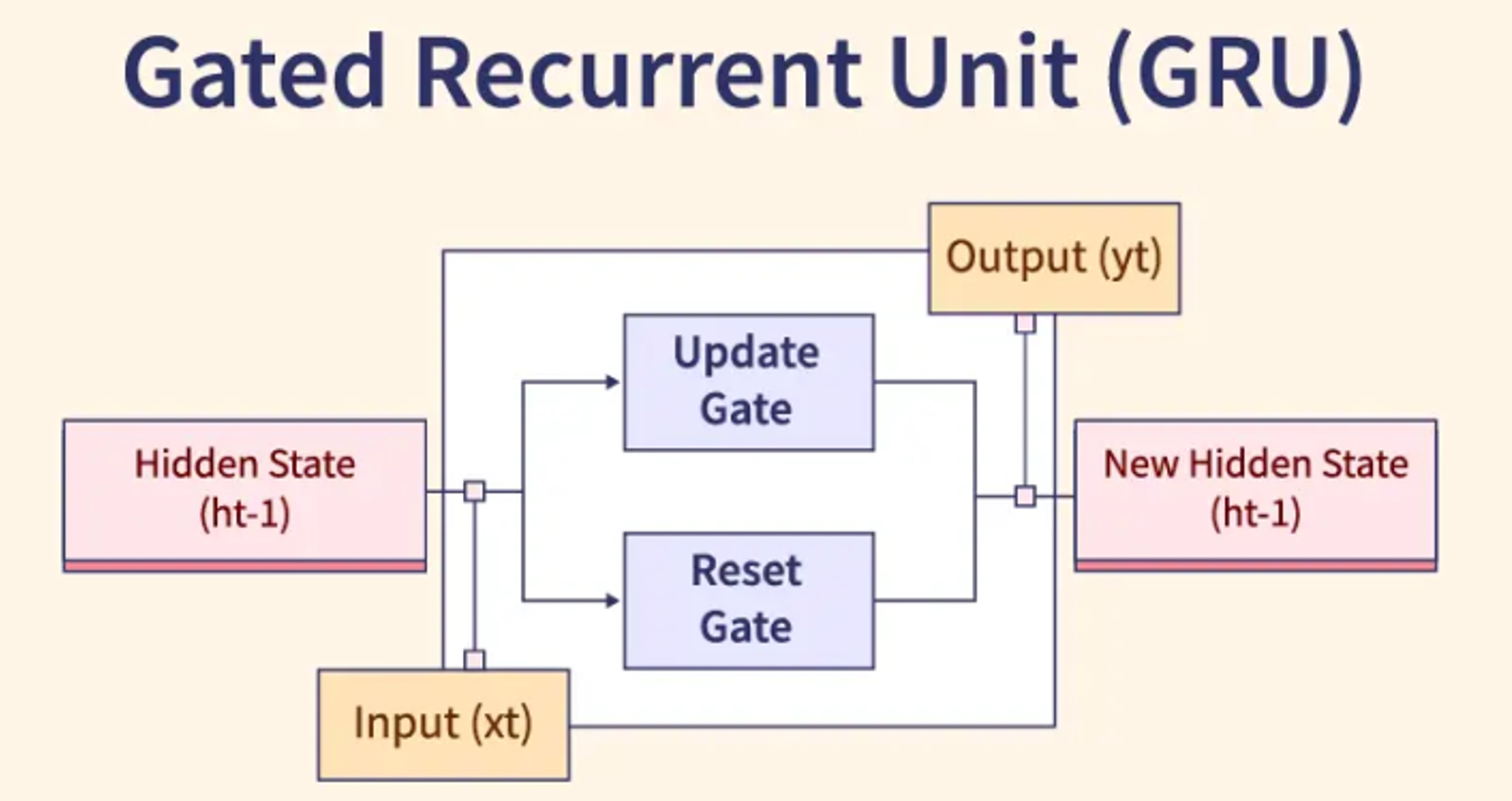
#29

★★★

注意力機制 (Attention Mechanism) 的計算

Transformer 核心

自注意力的核心計算涉及將輸入向量轉換為查詢 (Q)、鍵 (K)、值 (V) 三個向量（通常透過與權重矩陣相乘實現）。然後計算 Q 與所有 K 的點積相似度，經過 Softmax 歸一化得到注意力權重，最後用這些權重對 V 進行加權求和。整個過程是密集的矩陣/向量運算。

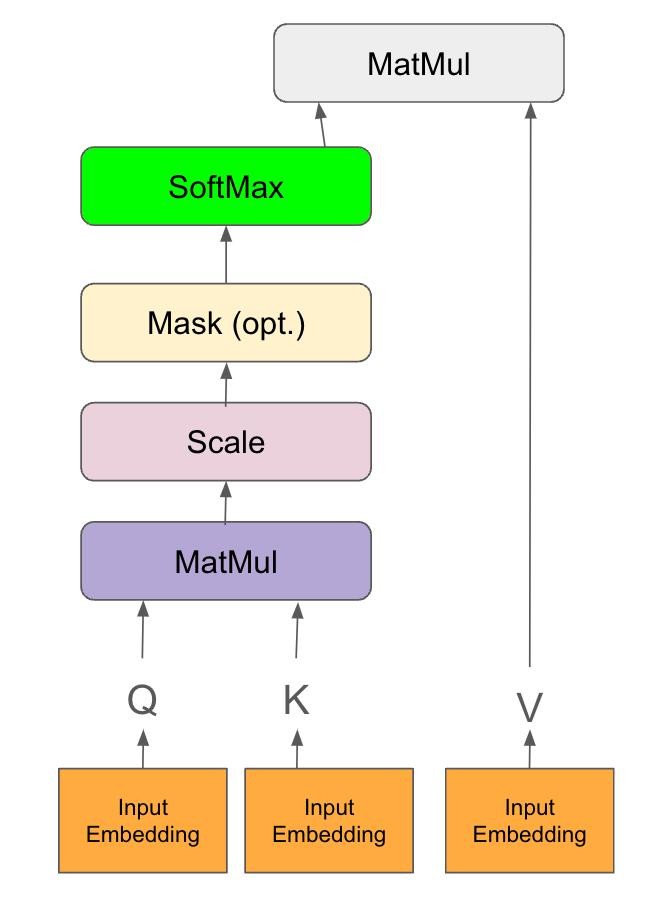
#30

★★★★

NumPy - Python 數值計算基礎庫

核心函式庫

NumPy (Numerical Python) 是 Python 中進行科學計算的基礎套件。它提供了高效的多維陣列對象（ndarray）以及對這些陣列進行操作的各種函數（包括線性代數運算、傅立葉轉換、隨機數生成等）。是許多機器學習庫（如 Scikit-learn, TensorFlow, PyTorch）的底層依賴。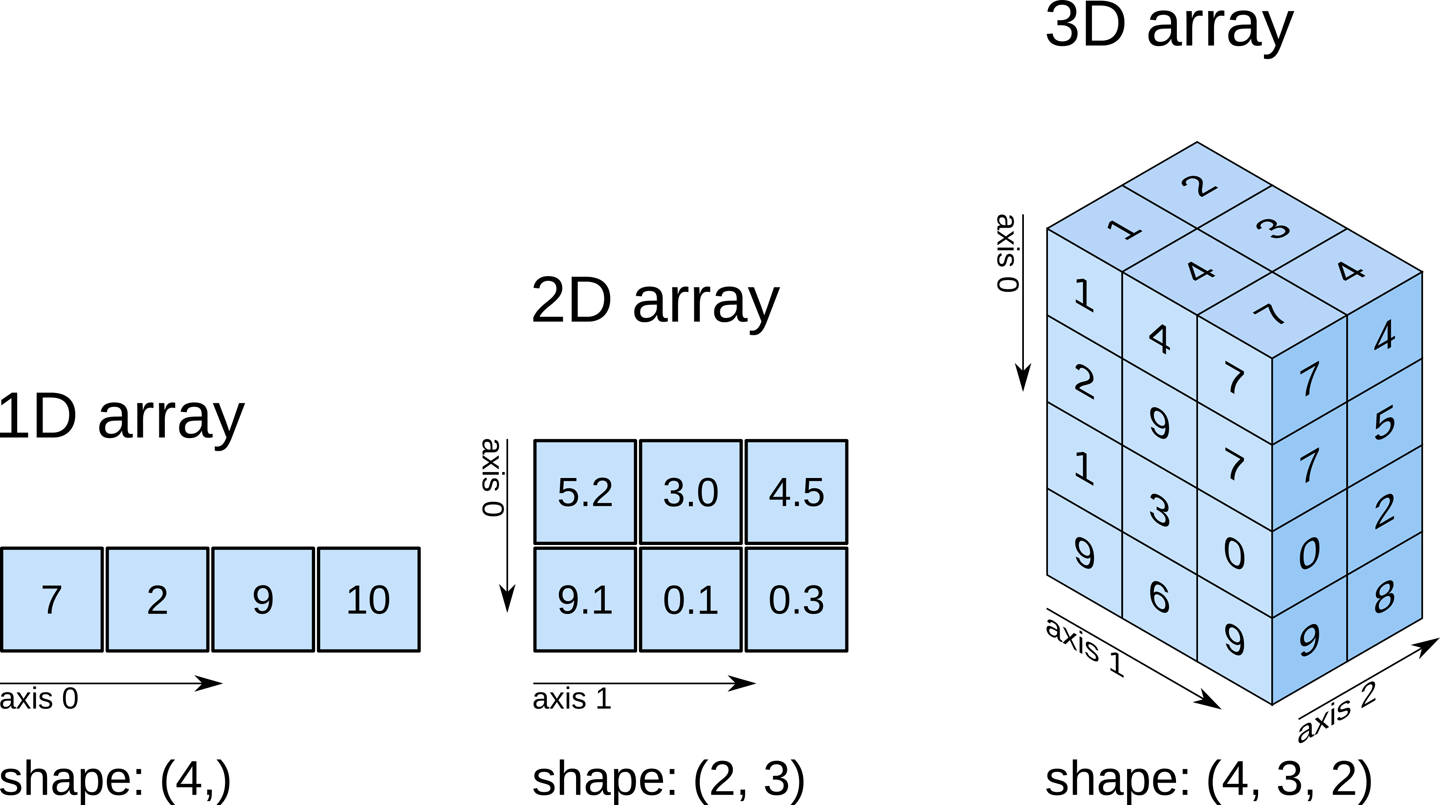

#31

★★★

深度學習框架 (TensorFlow, PyTorch) 中的線性代數

框架支持

像 TensorFlow 和 PyTorch 這樣的深度學習框架，其核心就是圍繞張量 (Tensor) 操作構建的。它們提供了高度優化的線性代數運算實現（可在 CPU 或 GPU 上運行），並支持自動微分，極大地方便了神經網路等模型的構建和訓練。

#32

★★★

數值穩定性 (Numerical Stability)

計算考量

在進行線性代數運算（尤其是在深度學習的多次迭代中）時，需要考慮數值穩定性問題。例如，梯度消失/爆炸、浮點數精度問題可能導致計算結果不準確或溢出。選擇合適的算法、激活函數、正規化方法有助於提高數值穩定性。

#33

★★

線性組合 (Linear Combination) 與線性獨立 (Linear Independence)

基本概念

線性組合：一組向量的線性組合是指將這些向量分別乘以某個純量後再相加得到的向量。
線性獨立：如果一組向量中沒有任何一個向量可以表示為其他向量的線性組合，則稱這組向量是線性獨立的。

這些概念是理解向量空間、基、秩等概念的基礎。

#34

★★

向量外積 (Outer Product)

向量運算

兩個向量 u (m×1) 和 v (n×1) 的外積是一個 m×n 的矩陣，計算方式為 uvᵀ。其結果矩陣的秩為 1（如果 u, v 非零）。在某些機器學習應用（如協方差矩陣估計、某些神經網路更新規則）中會用到。

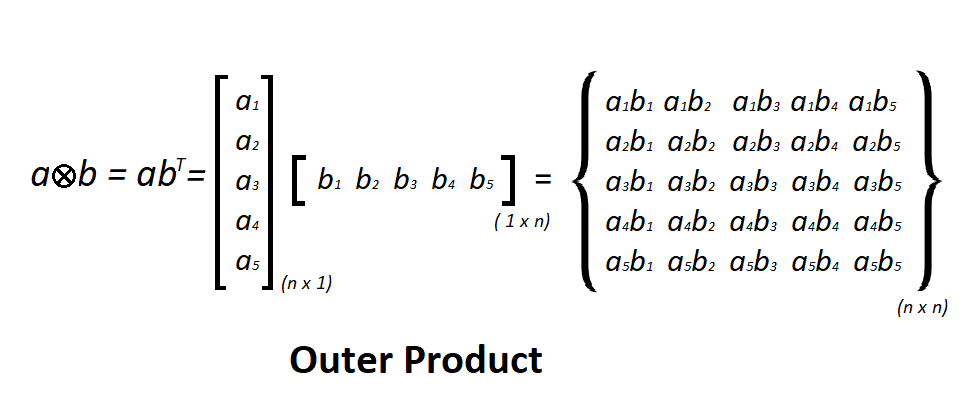
#35

★★

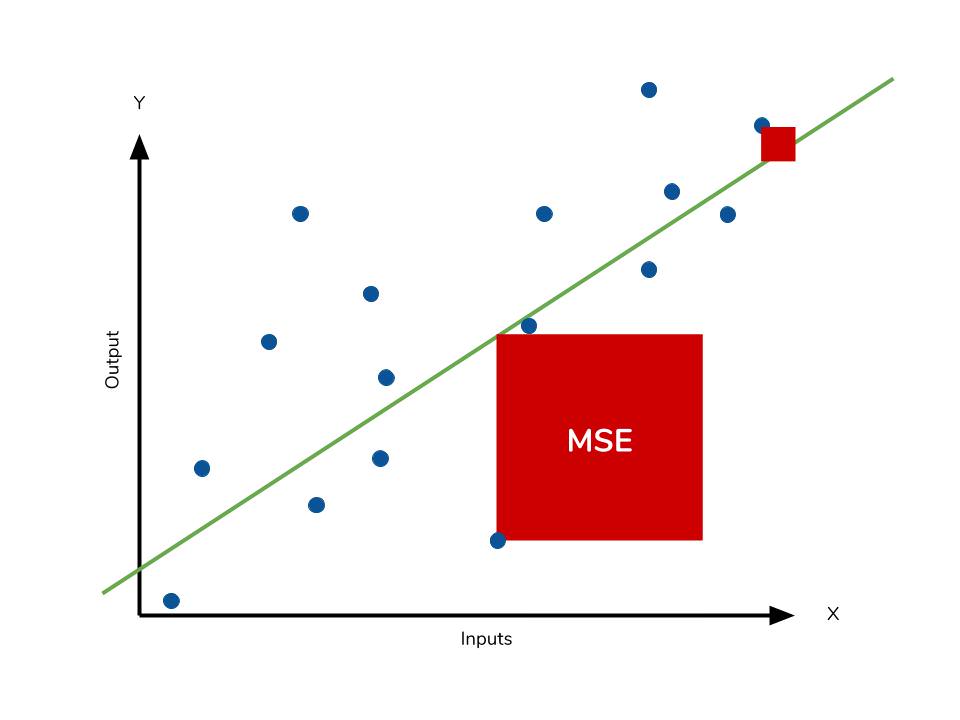
最小二乘法 (Least Squares)

優化方法

最小二乘法是求解線性迴歸問題的常用方法，其目標是最小化預測值與實際值之間誤差的平方和（即 MSE 損失）。正規方程是最小二乘法的一個解析解。

#36

★★

協方差矩陣 (Covariance Matrix)

統計矩陣

表示數據集中不同特徵之間線性關係強度和方向的方陣。對角線元素是各特徵的變異數，非對角線元素是特徵之間的協方差。PCA 就是對協方差矩陣（或相關係數矩陣）進行特徵分解。

#37

★★

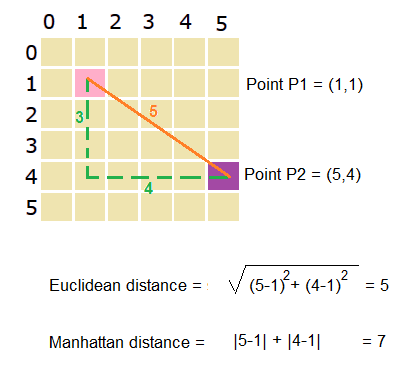
曼哈頓距離 (Manhattan Distance) / L1 距離

距離度量

衡量兩個向量之間距離的另一種方式，計算公式為兩向量差向量的 L1 範數：d(u, v) = ||u - v||₁ = Σ |uᵢ - vᵢ|。表示沿著坐標軸移動的總距離。

#38

★★

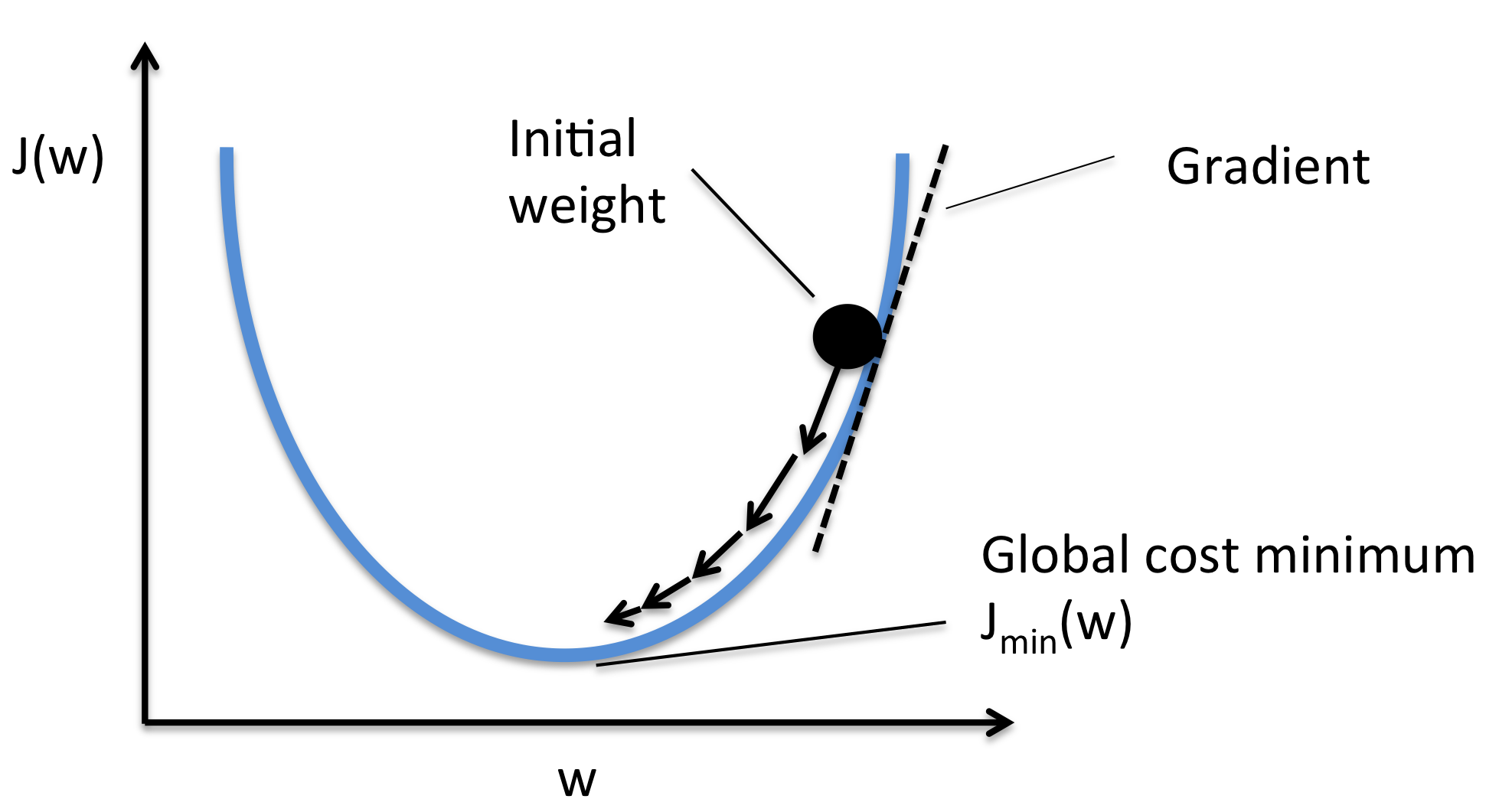
梯度 (Gradient) 的向量本質

向量微積分

梯度本身就是一個向量，其方向指向函數值增加最快的方向，其大小（範數）表示增加的速率。理解梯度是向量，有助於理解梯度下降法中參數更新的方向和步長。

#39

★★

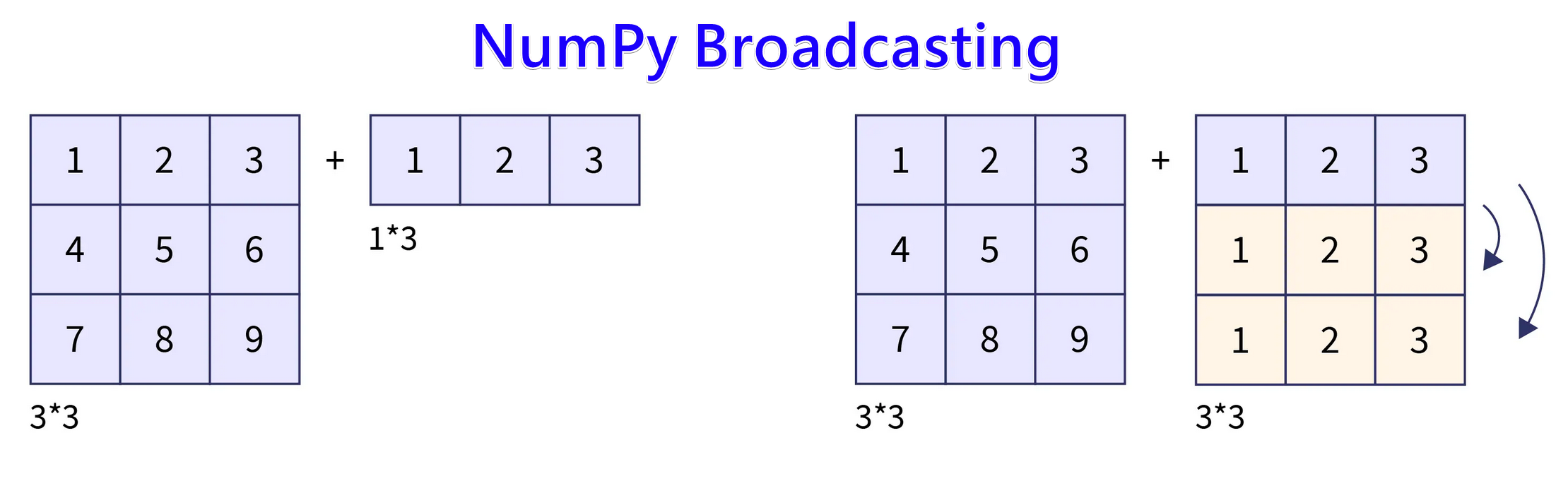
廣播 (Broadcasting) 機制

NumPy/框架特性

NumPy 和深度學習框架中的一種機制，允許對不同形狀的陣列（向量、矩陣）執行逐元素運算，自動擴展較小陣列的維度以匹配較大陣列。例如，將一個向量加到矩陣的每一行。簡化了程式碼編寫。

#40

★

對稱矩陣 (Symmetric Matrix)

特殊矩陣

一個方陣 A 如果等於其轉置 (A = Aᵀ)，則稱為對稱矩陣。協方差矩陣是典型的對稱矩陣。對稱矩陣具有良好的性質（如保證可以對角化）。

#41

★

矩陣的跡 (Trace)

矩陣運算

方陣主對角線元素之和。記為 tr(A)。具有循環不變性 tr(ABC) = tr(CAB) = tr(BCA)。

#42

★

行列式 (Determinant)

矩陣性質

方陣的一個純量值，表示矩陣對應的線性變換對空間體積的縮放比例。行列式不為零是方陣可逆的充要條件。

#43

★

低秩近似 (Low-Rank Approximation)

降維應用

使用一個秩較低的矩陣來近似原始矩陣。可以透過 SVD 實現，保留最大的 k 個奇異值及其對應的奇異向量來構建低秩矩陣。用於數據壓縮、去噪、推薦系統。

#44

★

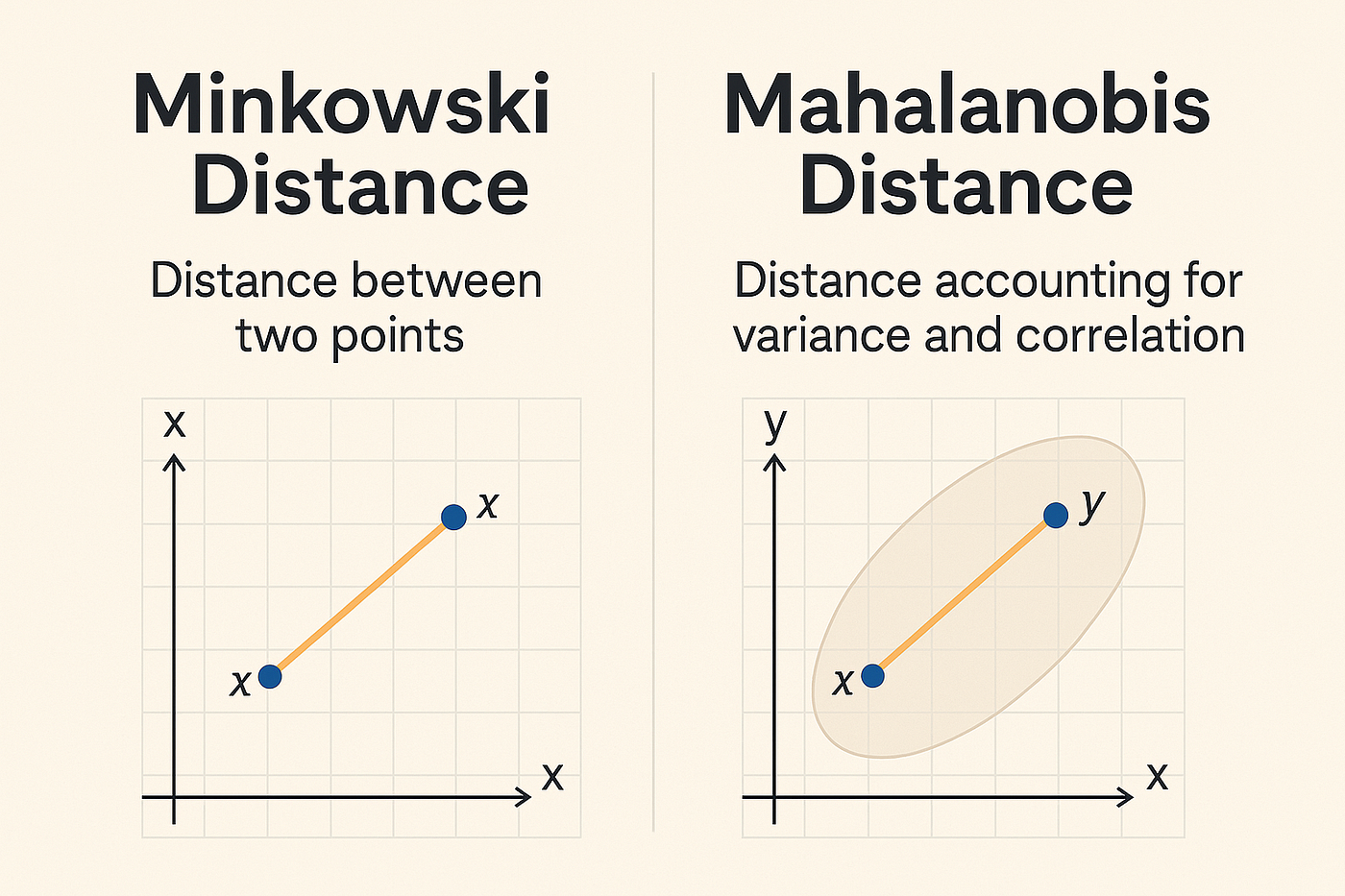
馬氏距離 (Mahalanobis Distance)

距離度量

考慮了數據協方差的距離度量。它對數據進行了白化（去除相關性並標準化變異數）後再計算歐幾里得距離。適用於特徵相關且尺度不同的情況。

#45

★

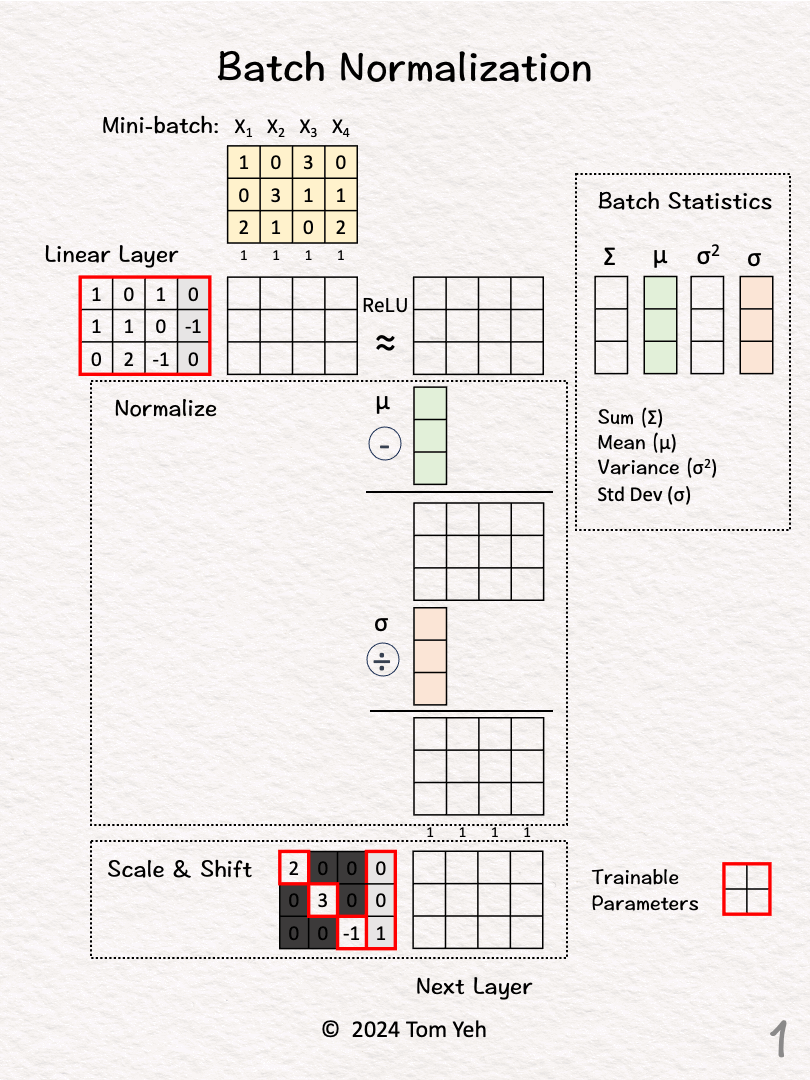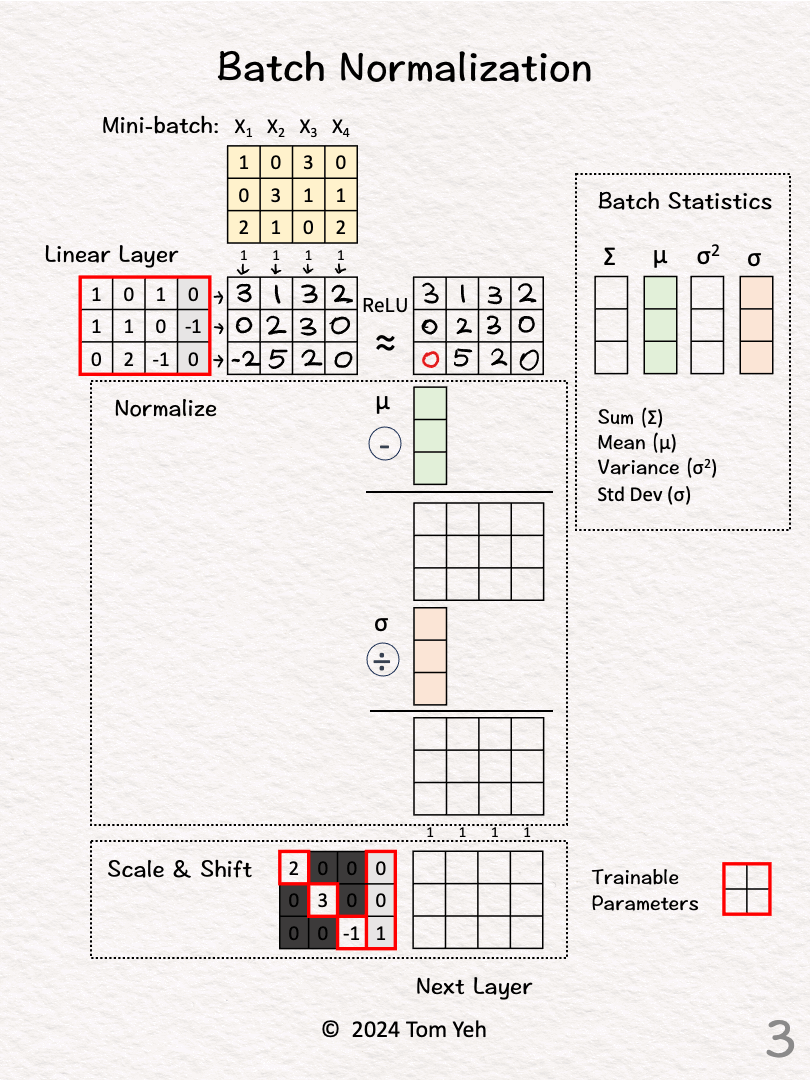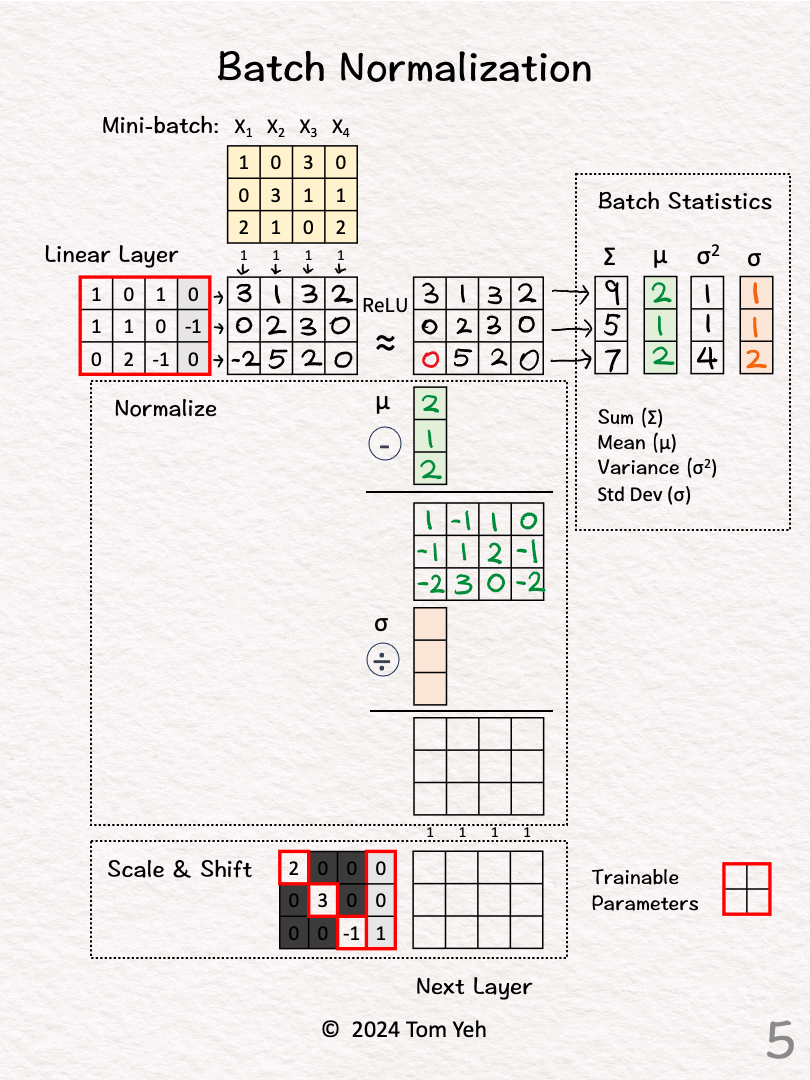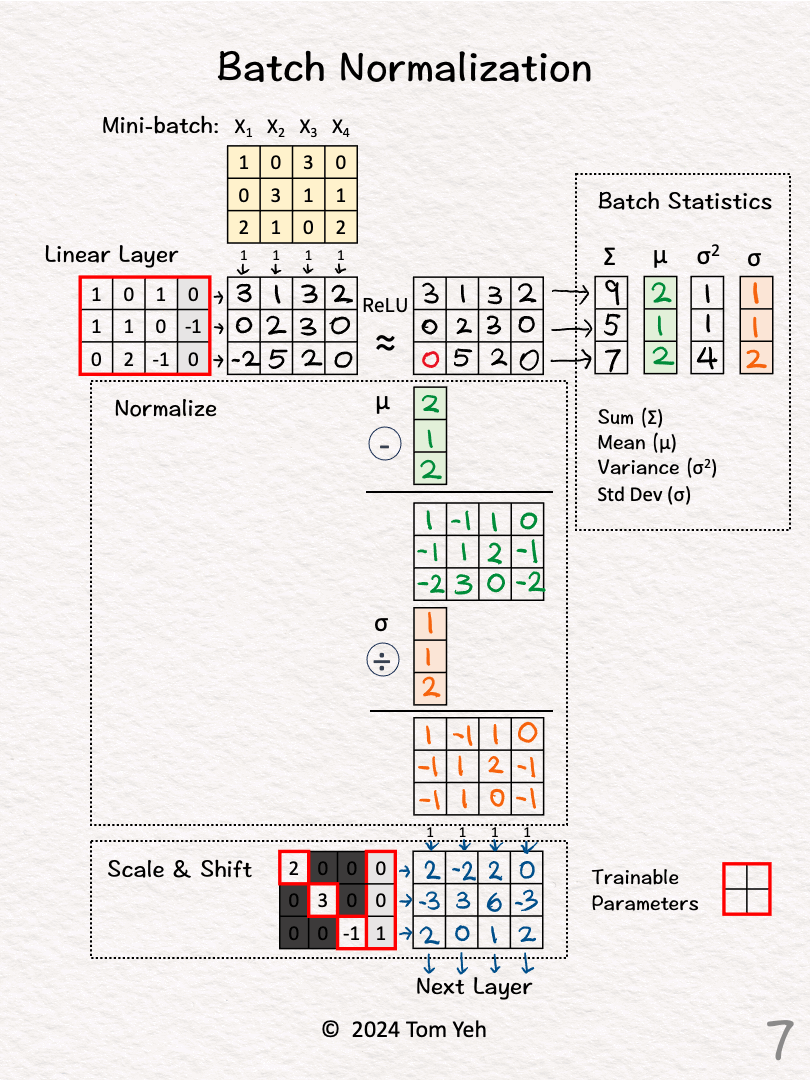
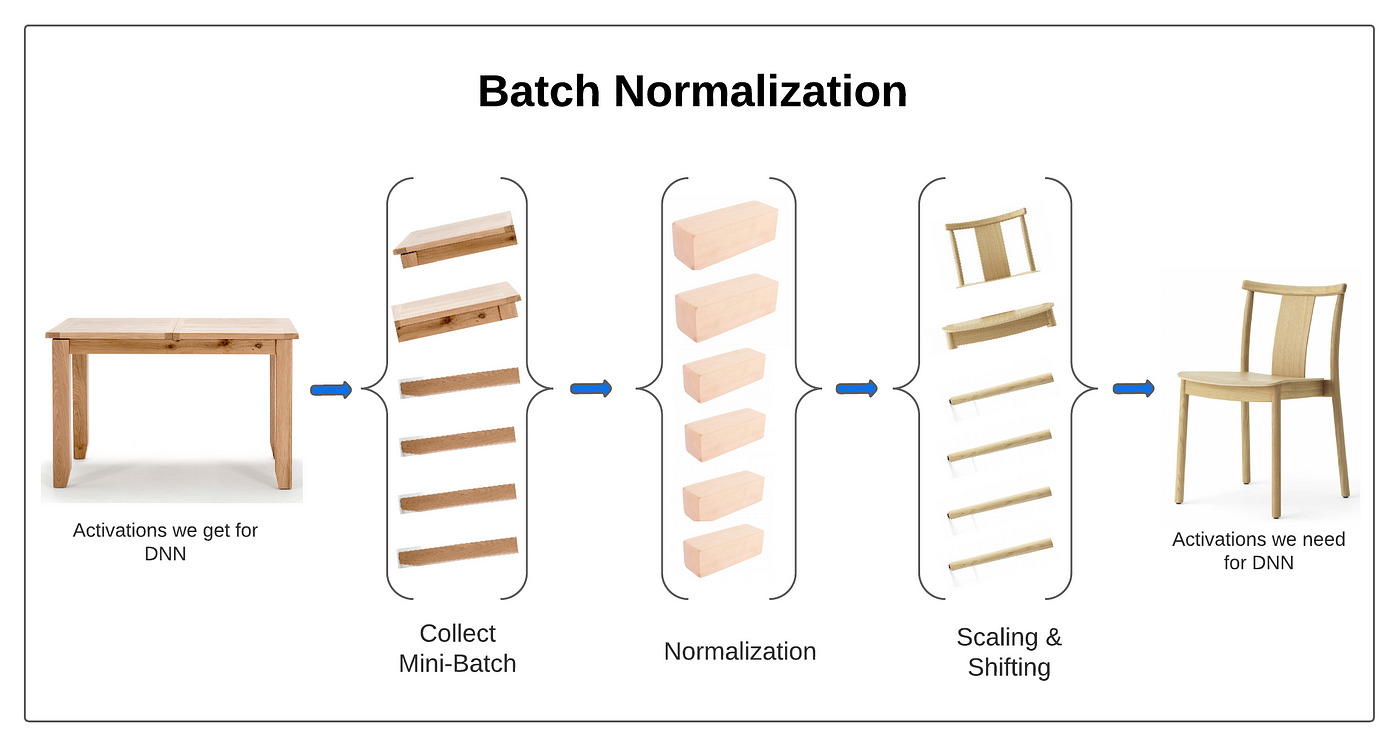
批次正規化 (Batch Normalization) 的計算

神經網路計算

涉及計算一個小批次數據在某層激活前的均值和變異數，然後用它們來標準化該批次的數據。標準化後還會進行縮放和平移（使用可學習的 γ 和 β 參數）。

#46

★

稀疏矩陣 (Sparse Matrix)

數據結構

指大部分元素為零的矩陣。在處理文本（如詞袋模型）、社交網路等數據時很常見。需要使用專門的數據結構和算法（如 SciPy 中的 sparse 模塊）來高效地儲存和運算。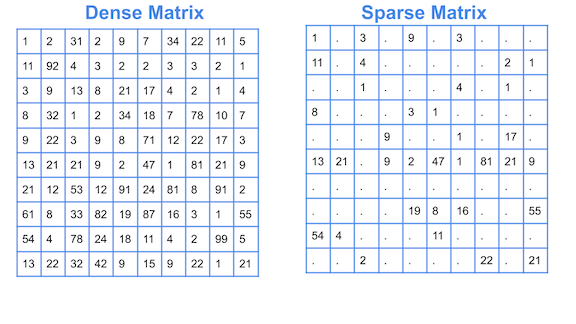

#47

★

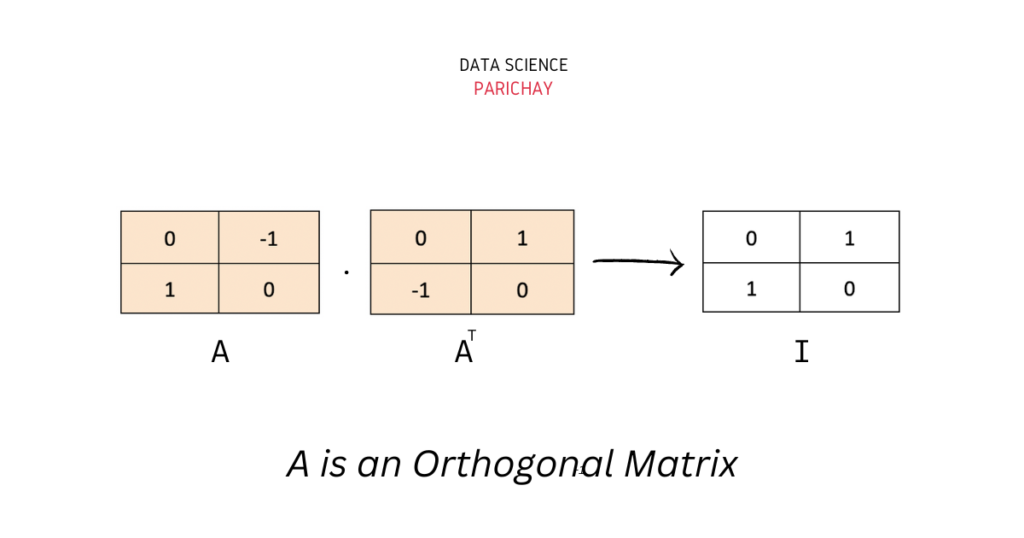
正交矩陣 (Orthogonal Matrix)

特殊矩陣

一個方陣 Q 如果其轉置等於其逆矩陣 (QᵀQ = QQᵀ = I)，則稱為正交矩陣。其列向量（和行向量）構成一組標準正交基。正交變換保持向量長度和角度不變（如旋轉、反射）。SVD 分解中的 U 和 V 都是正交矩陣。

#48

★

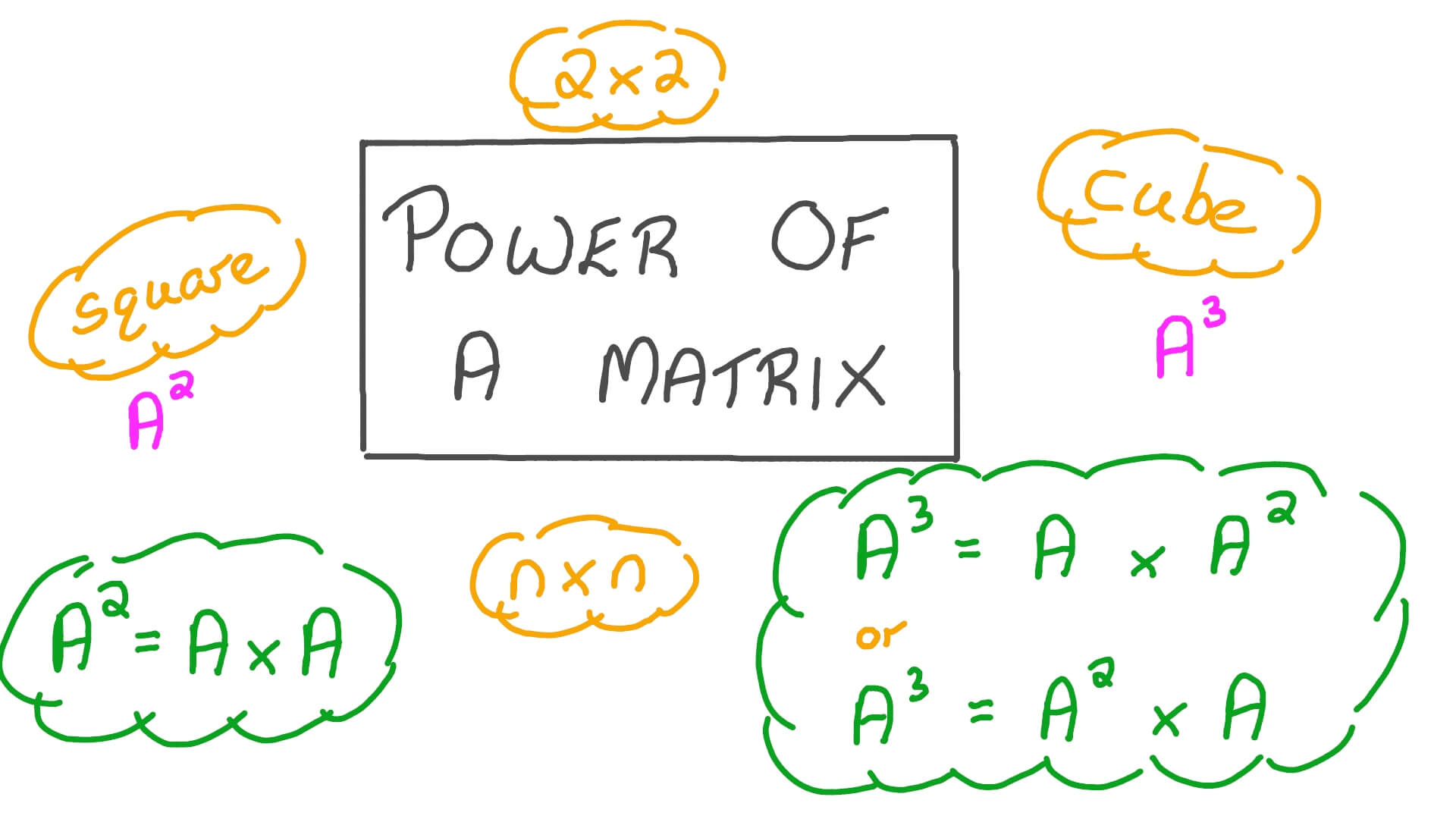
矩陣的冪 (Matrix Power)

矩陣運算

方陣 A 的 k 次冪 Aᵏ 是指將 A 自乘 k 次。在某些動態系統或圖算法（如計算可達性）中可能用到。可以透過特徵分解來加速計算（如果可對角化）。

#49

★

線性相關 (Linear Dependence) / 共線性 (Collinearity)

數據問題

指數據集中的某些特徵可以由其他特徵線性表示。這會導致數據矩陣 (X) 或 XᵀX 矩陣秩虧，使得正規方程無法求解（矩陣不可逆），並可能導致迴歸係數估計不穩定。嶺迴歸有助於處理此問題。

#50

★

奇異值 (Singular Value) 的意義

SVD 組件

矩陣 A 的奇異值（SVD 中 Σ 矩陣的對角線元素）表示了矩陣 A 在對應奇異向量方向上對空間的拉伸程度。較大的奇異值對應於數據中更重要的變異方向。

#51

★

矩陣範數 (Matrix Norm)

概念

衡量矩陣大小的概念，類似向量範數。常見的有 Frobenius 範數（所有元素平方和的平方根）等。在某些進階 ML 理論或算法（如矩陣分解的正則化）中會用到。

#52

★

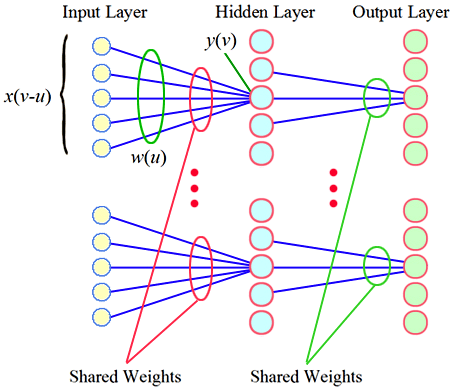
權重共享 (Weight Sharing)

CNN 特點

CNN 卷積層的關鍵特性。同一個卷積核（包含一組權重）在輸入的不同位置重複使用，大大減少了模型參數數量，提高了模型的平移不變性。

#53

★

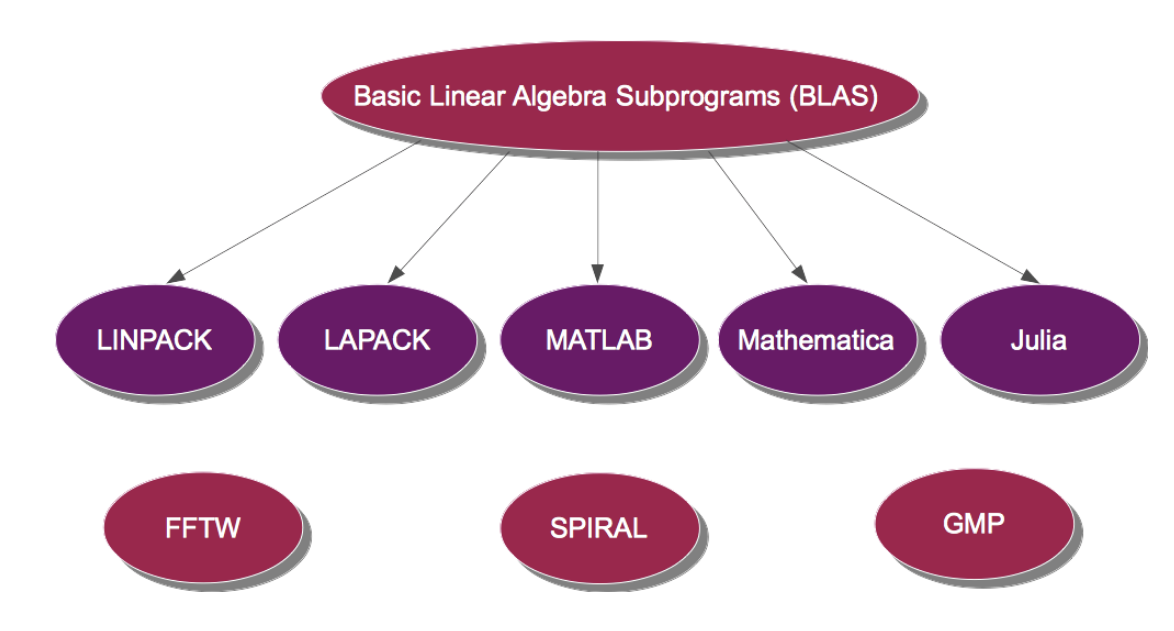
BLAS/LAPACK

底層庫

BLAS (Basic Linear Algebra Subprograms) 和 LAPACK (Linear Algebra PACKage) 是提供底層、高性能線性代數運算（如矩陣乘法、求解線性方程組、矩陣分解）的標準接口和實現。許多科學計算庫（包括 NumPy）會依賴它們。

#54

★

向量空間 (Vector Space)

數學結構

由向量構成的集合，滿足特定的加法和純量乘法封閉性及運算規則。是線性代數的基本研究對象。

#55

★

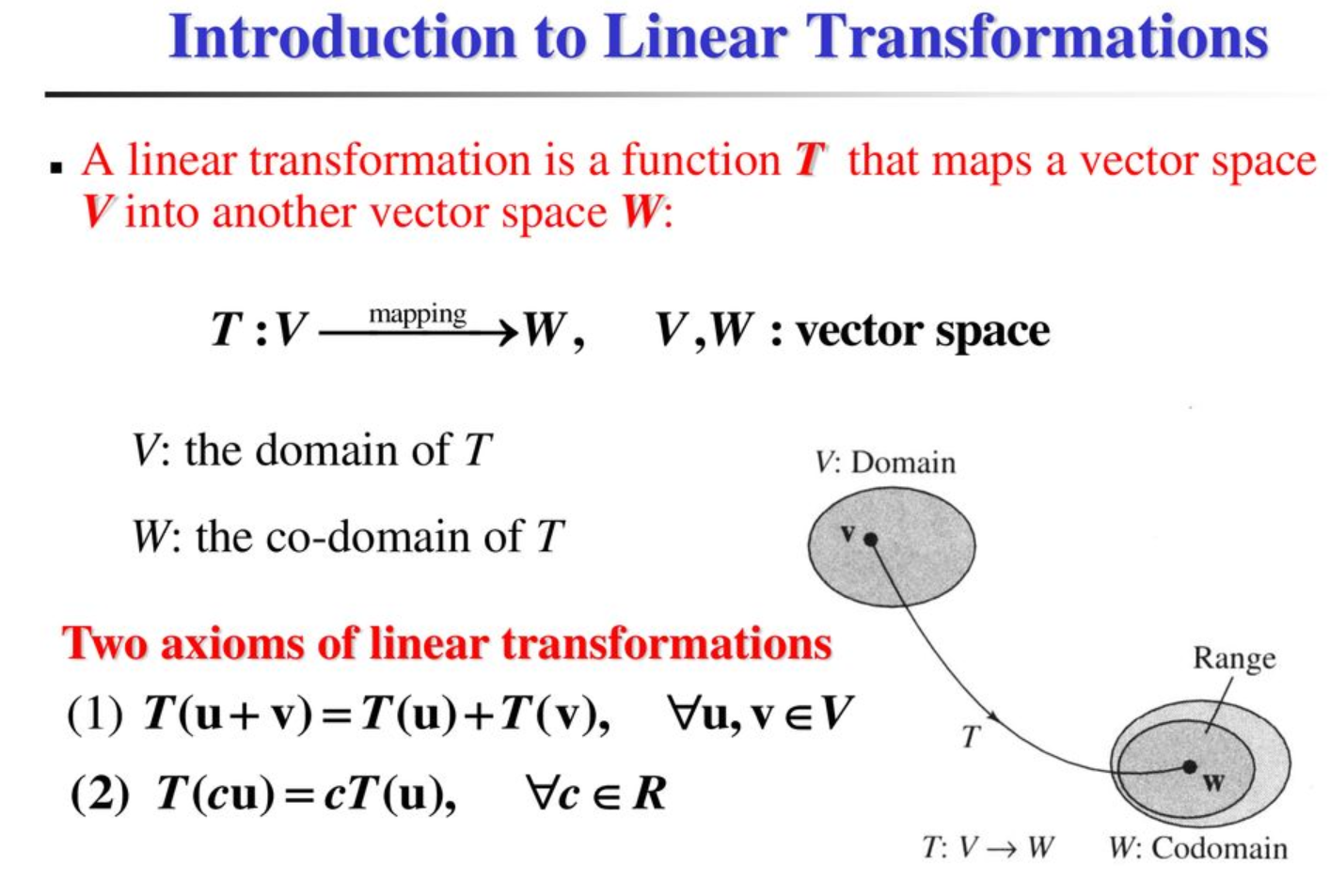
線性變換 (Linear Transformation)

概念

保持向量加法和純量乘法運算的函數（映射）。任何有限維向量空間之間的線性變換都可以用矩陣乘法來表示。

#56

★

解線性方程組的方法 (高斯消去)

數值方法

高斯消去法是求解線性方程組 Ax=b 的一種經典直接法。雖然 ML 中更常用迭代法（如梯度下降）或直接求逆（正規方程），但理解基本求解方法有助於建立概念。

#57

★

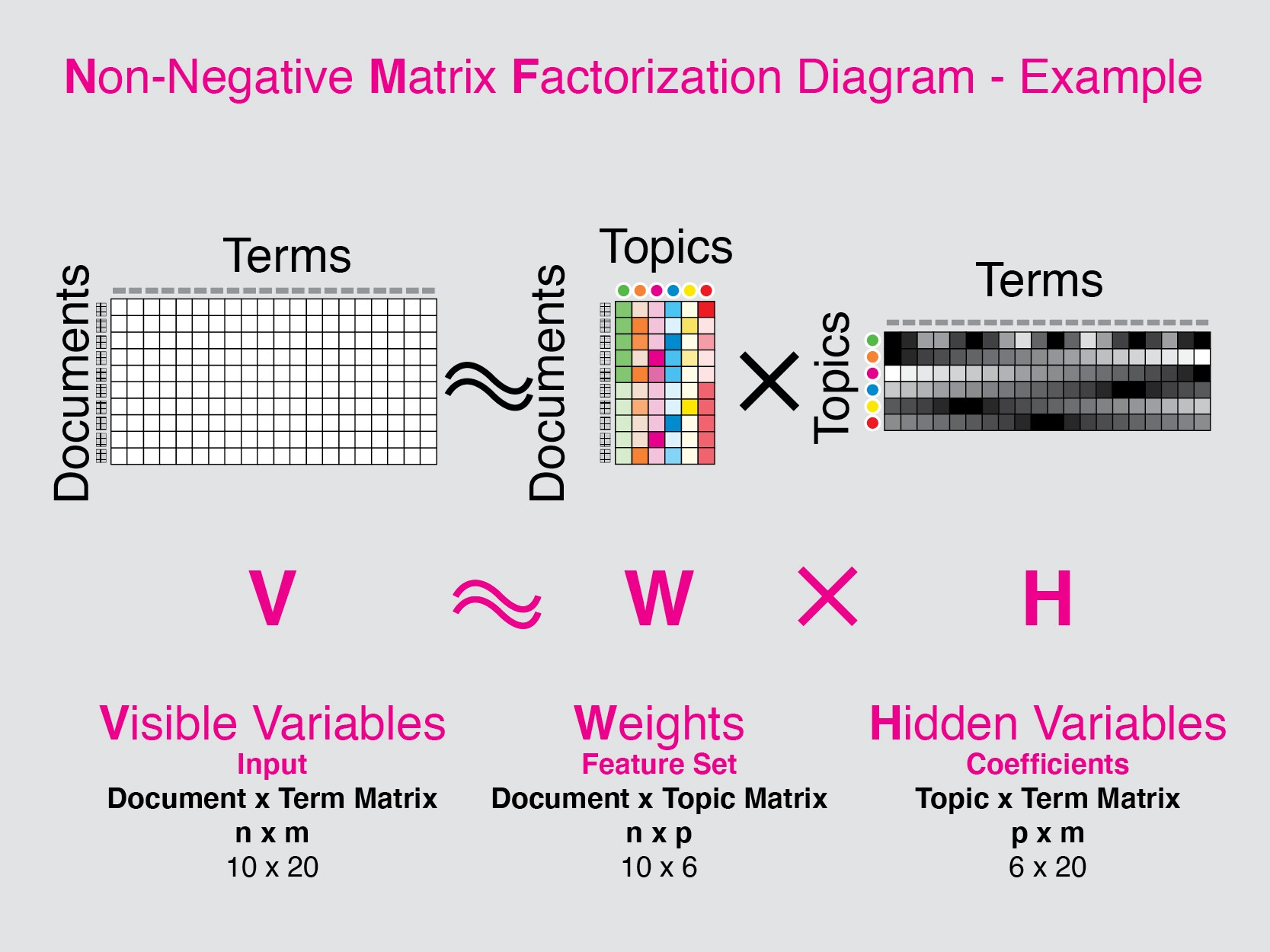
非負矩陣分解 (NMF, Non-negative Matrix Factorization)

矩陣分解

一種矩陣分解技術，將一個非負矩陣分解為兩個非負矩陣的乘積。常用於主題模型、圖像分析、推薦系統等，其結果通常具有較好的可解釋性（加性組合）。

#58

★

向量正交性 (Orthogonality)

向量關係

如果兩個非零向量的點積為零，則稱它們是正交的（幾何上垂直）。正交基在PCA等變換中很重要。

#59

★

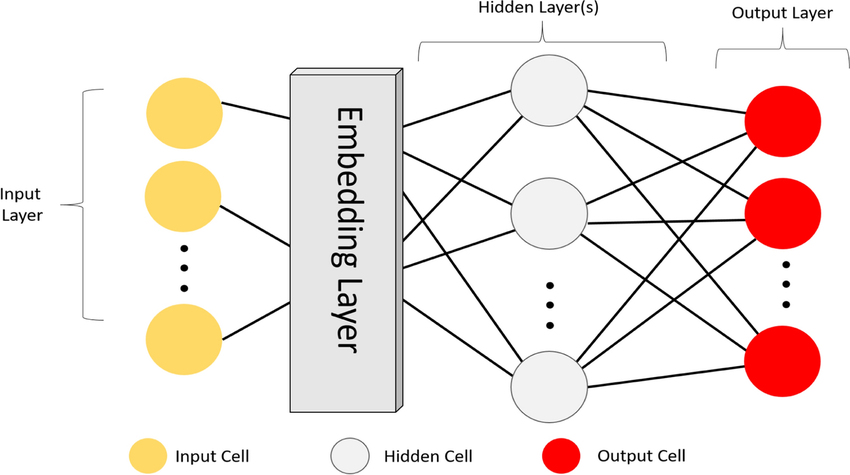
嵌入層 (Embedding Layer)

神經網路層

常用於處理離散類別輸入（如單詞索引）的神經網路層。它將每個離散輸入映射到一個低維、稠密的向量表示（嵌入向量）。本質上是一個可學習的查找表（矩陣）。

#60

★

硬體加速線性代數運算 (Hardware Accelerated Linear Algebra Computing)

硬體加速

不同硬體架構在深度學習運算中的比較：

硬體類型	特點	適用場景	代表產品
中央處理器 (Central Processing Unit, CPU)	通用處理器，單核心性能強，但並行度低	小規模運算、串行任務	Intel Core, AMD Ryzen
圖形處理器 (Graphics Processing Unit, GPU)	大量並行處理核心，適合矩陣運算	深度學習訓練、圖形處理	NVIDIA RTX, AMD Radeon
神經網路處理器 (Neural Processing Unit, NPU)	專為神經網路優化，能效比高	移動設備AI運算	華為昇騰、高通Hexagon
張量處理器 (Tensor Processing Unit, TPU)	Google專為深度學習設計，矩陣運算極快	大規模AI訓練、推論	Google TPU v4

在深度學習領域，GPU (Graphics Processing Unit) 因其大量並行處理核心，特別適合執行大規模的矩陣和向量運算，能夠極大地加速模型訓練和推論。像 CUDA Basic Linear Algebra Subprograms (cuBLAS) (NVIDIA 的 BLAS 實現) 提供了底層支持。

iPAS AI應用規劃師 考試重點

iPAS AI應用規劃師考試重點