iPAS AI應用規劃師 考試重點

L22301 統計學在大數據中的應用
主題分類
1
大數據特性與統計挑戰
2
抽樣方法在大數據的應用
3
降維技術 (統計觀點)
4
A/B 測試與實驗設計
5
統計學習概論
6
分散式計算與統計
7
大數據視覺化與洞察
8
統計在機器學習中的角色
#1
★★★★★
大數據 (Big Data) 的 V 特性
核心特性 (常見 3V/5V)
理解大數據的特性是應用統計方法的基礎：
  • 資料量 (Volume)：數據規模極大，遠超傳統工具處理能力 (TB, PB, EB 等級)。
  • 速度 (Velocity)：數據產生和流動速度快，需要即時或近乎即時的處理。
  • 多樣性 (Variety)：數據來源和格式多樣，包含結構化、半結構化和非結構化數據。
  • (其他常見 V)：真實性 (Veracity) - 數據品質和可信度；價值 (Value) - 從數據中提取有價值的洞見。
Q4 考察了大數據時代資料的特性。
#2
★★★★★
傳統統計方法在大數據下的挑戰
主要限制
傳統統計方法在設計時並未考慮大數據的特性，面臨挑戰：
  • 計算限制 (Computational Limit)：許多傳統算法在單機上無法處理龐大的數據量。
  • 記憶體限制 (Memory Limit)：數據無法完全載入單機記憶體。
  • 演算法擴展性 (Algorithmic Scalability)：某些算法的時間複雜度隨數據量增長過快。
  • 統計顯著性問題 (Statistical Significance)：在大數據中，微小的差異也可能達到統計顯著 (p值很小)，但缺乏實際意義。
  • 高維度挑戰 (High Dimensionality)：變數數量可能非常多（維度災難）。
  • 非結構化數據：傳統方法主要針對結構化數據。
#3
★★★★
抽樣 (Sampling) 在大數據中的必要性
為何需要抽樣
儘管擁有全部數據，抽樣在大數據分析中仍有其價值：
  • 降低計算成本：在樣本上進行探索性分析、模型開發和測試，速度更快、成本更低。
  • 快速迭代：可以在樣本上快速驗證想法和調整模型。
  • 數據標註：對全部大數據進行標註成本過高，可在樣本上進行標註。
  • 某些推論場景：統計推論本身就是基於樣本推論母體。
但需注意抽樣方法必須能確保樣本的代表性。
#4
★★★★
大數據抽樣方法 - 簡單隨機抽樣 (Simple Random Sampling)
方法與挑戰
  • 方法：母體中每個個體被抽中的機率完全相等。
  • 挑戰：在大數據環境下，對整個數據集進行隨機選擇可能效率低下或不可行（如流式數據）。需要適用於分散式環境的抽樣演算法。
#5
★★★
大數據抽樣方法 - 分層抽樣 (Stratified Sampling)
方法與適用
  • 方法：先將母體依據某些特徵（如地區、年齡層）分成若干互斥的層 (Strata)，然後從每一層中獨立進行簡單隨機抽樣。
  • 優點：可以確保樣本在各層中的代表性，尤其當某些層的比例較小時；可以提高估計的精確度。
  • 挑戰：需要預先知道分層變數，且在分散式環境下執行可能較複雜。
#6
★★★
大數據抽樣方法 - 系統抽樣 (Systematic Sampling)
方法
  • 方法：先隨機選取一個起始點，然後每隔固定間隔 (k) 選取一個樣本。
  • 優點：操作簡單，易於在流式數據或大型數據庫中實現。
  • 缺點：如果數據存在週期性，且抽樣間隔恰好等於或為週期的倍數，可能產生偏差。
#7
★★
大數據抽樣方法 - 蓄水池抽樣 (Reservoir Sampling)
適用場景
蓄水池抽樣是一系列演算法，用於從一個未知大小或過於龐大（無法一次性載入記憶體）的數據流或數據集合中，抽取固定大小 k 的簡單隨機樣本。
  • 特性：只需要對數據進行一次遍歷。
  • 應用：非常適合處理流式數據 (Streaming Data) 的抽樣。
#8
★★★★★
降維 (Dimensionality Reduction) 的動機
為何需要降維
大數據通常具有高維度（大量特徵/變數）的特性，帶來挑戰：
  • 維度災難 (Curse of Dimensionality)：在高維空間中，數據點變得稀疏，距離度量失去意義，模型效能下降。
  • 計算複雜度：維度越高，模型訓練和預測所需的計算資源越多。
  • 模型過擬合 (Overfitting)：過多維度（尤其是不相關或冗餘的）可能導致模型過度擬合訓練數據。
  • 數據視覺化困難：人類難以視覺化超過三維的數據。
降維旨在用較少的維度來表示數據，同時保留大部分重要資訊。
#9
★★★★★
主成分分析 (Principal Component Analysis, PCA)
原理與目的
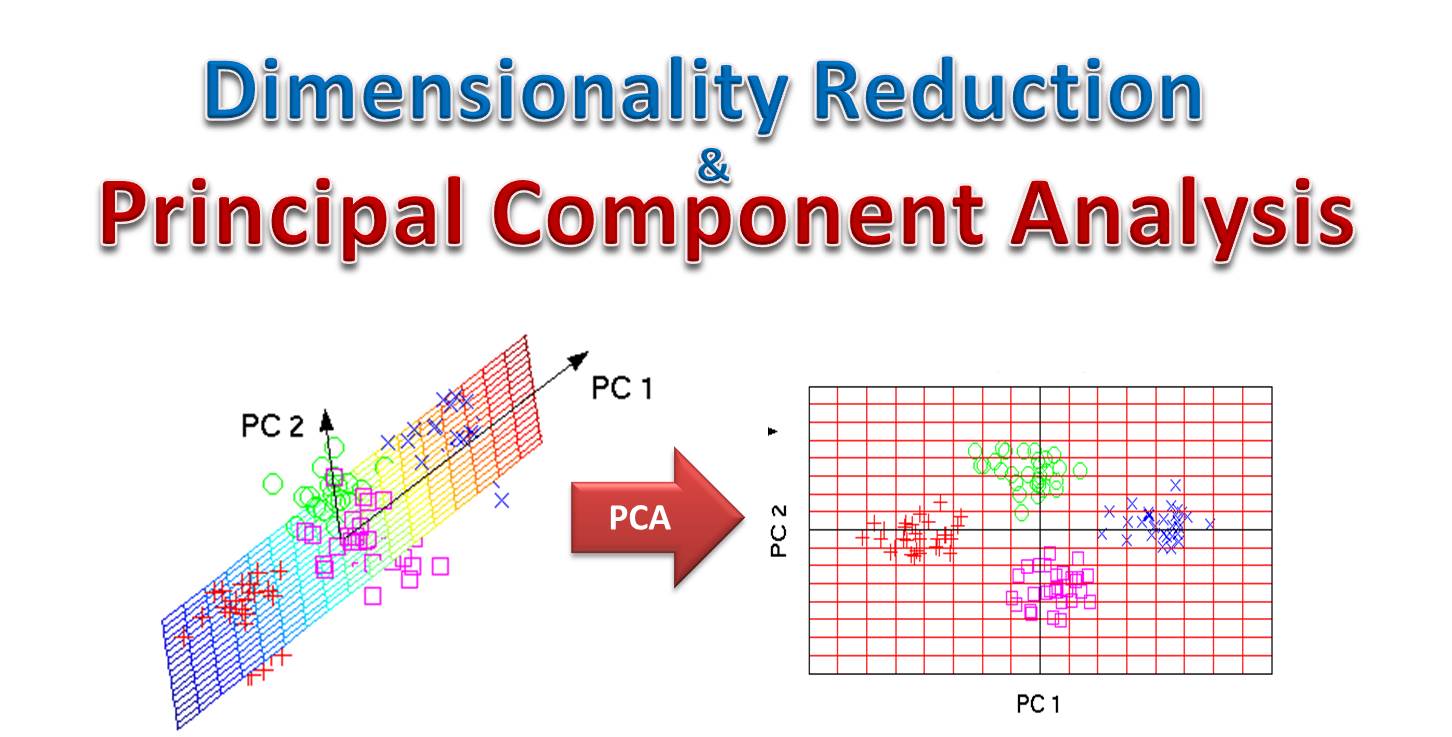
PCA 是一種常用的線性降維技術，也是一種無監督學習方法。
  • 目標：找到一組新的正交（互相垂直）軸（稱為主成分），使得數據在這些軸上的投影變異數最大化。
  • 過程：計算數據的共變異數矩陣 (Covariance Matrix)，找出其特徵值 (Eigenvalues) 和特徵向量 (Eigenvectors)。特徵向量代表主成分的方向，對應的特徵值代表數據在該方向上的變異量。
  • 降維：選取特徵值最大的前 k 個主成分作為新的維度，將原始數據投影到這 k 個軸上。
  • 優點：有效去除線性相關性，保留數據主要變異。
  • 缺點：新軸的解釋性可能較差；對數據尺度敏感（通常需要先標準化）；假設變數間為線性關係。
Q10 提到了 PCA。
#10
★★★
線性判別分析 (Linear Discriminant Analysis, LDA)
原理與目的
LDA 是一種監督式的線性降維技術，也可用於分類。
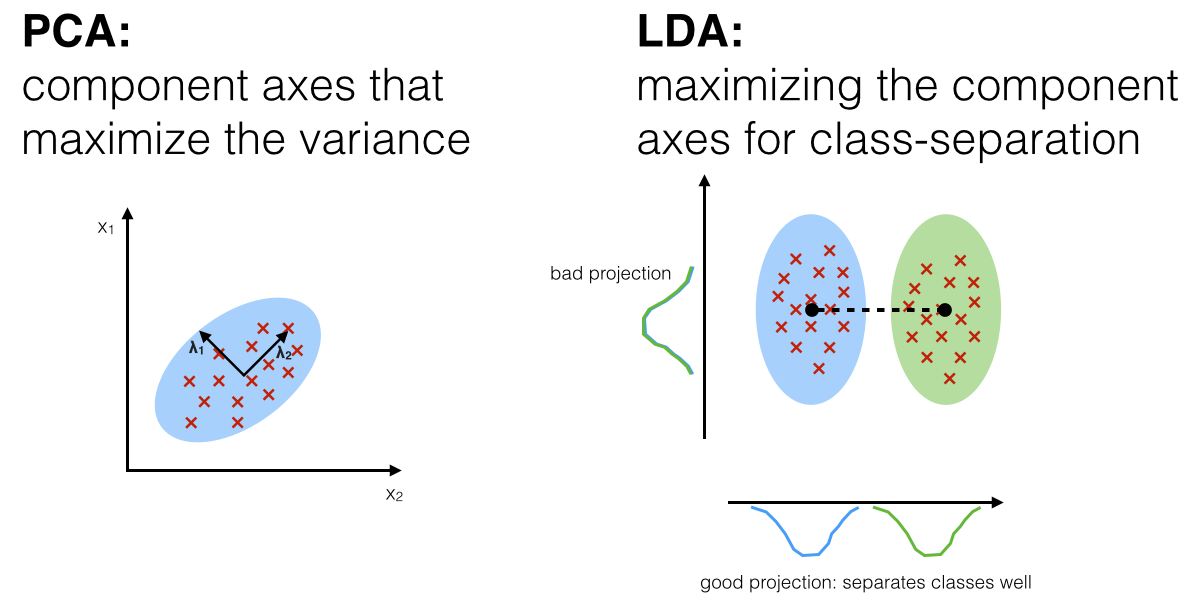
  • 目標：找到一個低維空間，使得原始數據投影後，不同類別之間的距離最大化，而同一類別內部的距離最小化。
  • 與 PCA 的區別：PCA 尋找最大化變異數的方向（無監督），而 LDA 尋找最有利於區分類別的方向（監督式，需要類別標籤）。
  • 應用：降維、人臉識別、圖像檢索。
  • 限制：降維後的維度最多為 C-1（C 為類別數）。
#11
★★
特徵選擇 (Feature Selection) vs 特徵提取 (Feature Extraction)
降維方式區別
兩者都是降維的方法：
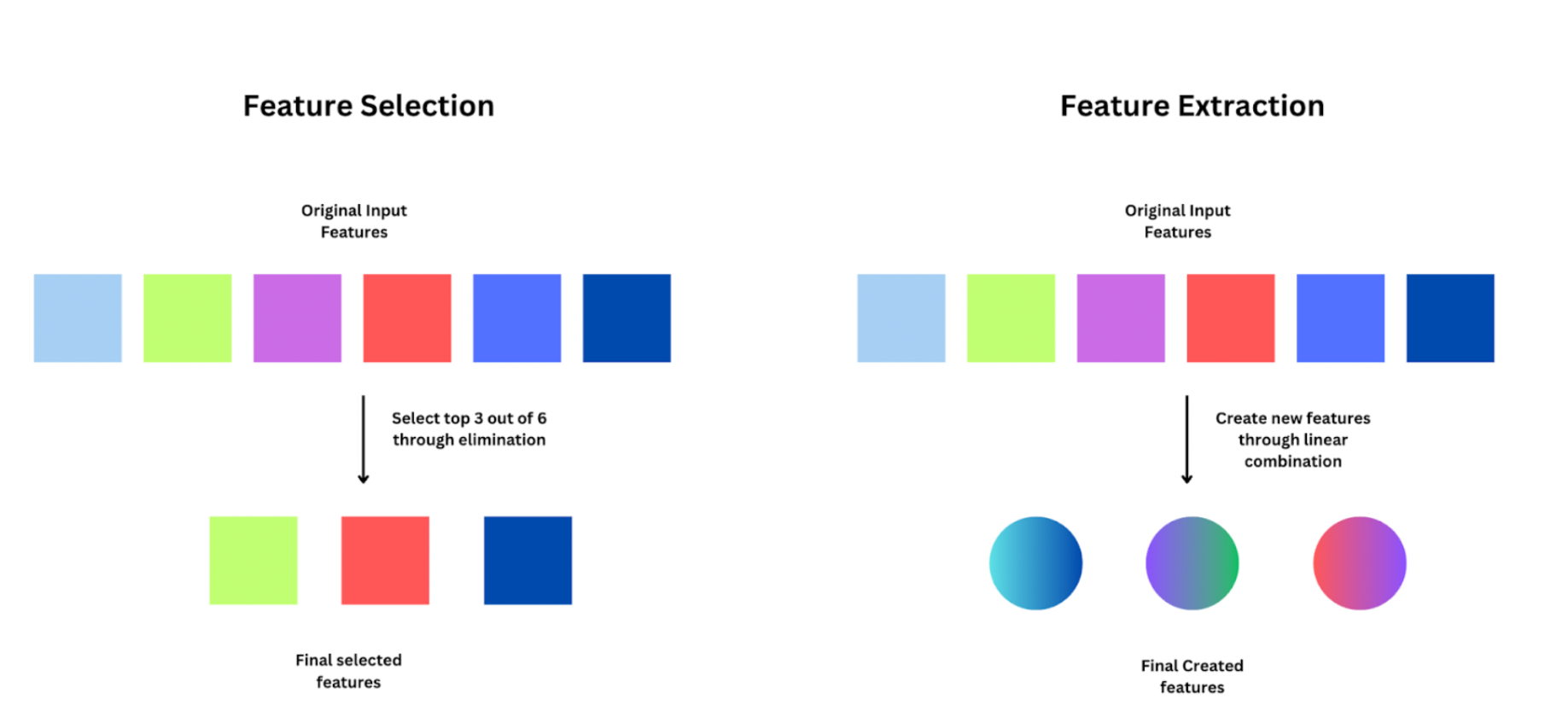
  • 特徵選擇：從原始特徵集合中，直接選取一個子集作為新的特徵。保留了原始特徵的可解釋性。方法如過濾法、嵌入法、包裝法。
  • 特徵提取：將原始特徵轉換或組合，生成一組新的、數量較少的特徵。新特徵可能不易解釋。例如：PCA, LDA。
Q8 區分了特徵工程中的不同概念。
#12
★★★★★
A/B 測試 (A/B Testing) - 基本概念
定義與目的
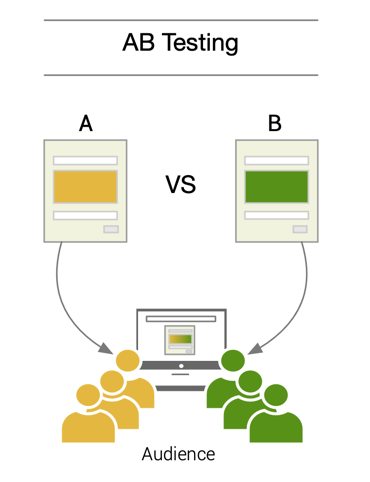
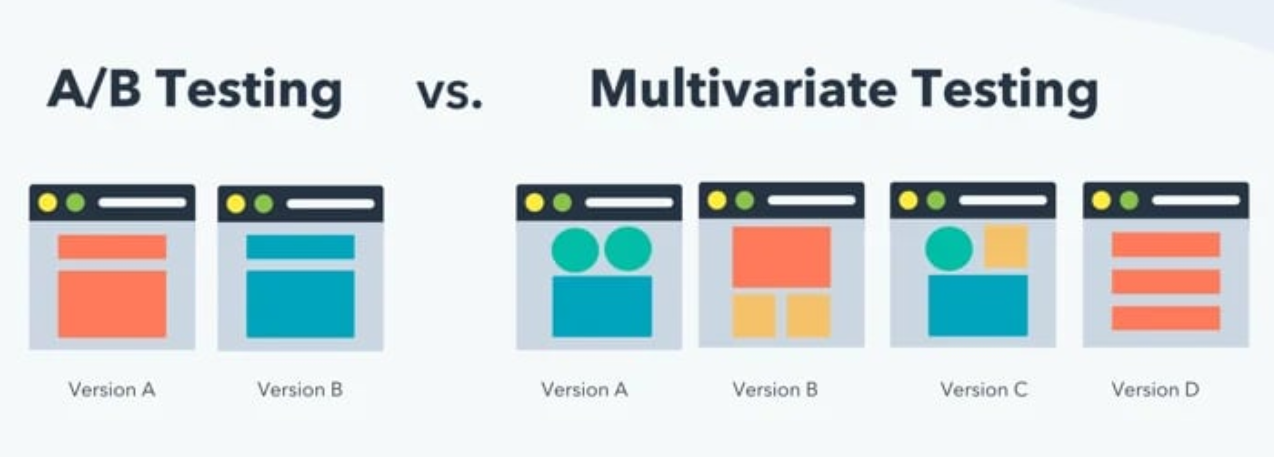
A/B 測試是一種對照實驗 (Controlled Experiment)，用於比較兩個版本（版本 A 和 版本 B）的效能差異。
  • 流程：將使用者隨機分配到兩個組別，一組看到版本 A（通常是對照組/原始版本），另一組看到版本 B（實驗組/新版本）。收集兩組在關鍵指標（如點擊率、轉換率、停留時間）上的表現數據。
  • 目的：透過統計假設檢定（如 t 檢定、Z 檢定）判斷版本 B 是否顯著優於版本 A。
  • 應用：網頁設計優化、廣告文案測試、推薦演算法比較、產品功能評估等。
#13
★★★★
A/B 測試中的假設檢定
應用流程
在 A/B 測試中應用假設檢定：
  • 設定假設：
    • H₀：兩個版本的指標沒有差異（如 p_A = p_B）。
    • H₁：兩個版本的指標有差異（如 p_A ≠ p_B 或 p_B > p_A）。
  • 選擇指標與檢定方法：根據指標類型（如比例、平均數）選擇合適的檢定（如 Z 檢定、t 檢定）。
  • 設定顯著水準 α (如 0.05)。
  • 收集足夠樣本數據。
  • 計算檢定統計量和 p 值。
  • 做出決策：若 p ≤ α，則拒絕 H₀，認為兩個版本有顯著差異。
#14
★★★
多變量測試 (Multivariate Testing, MVT)
與 A/B 測試區別
  • A/B 測試：比較兩個完整版本的效能。
  • 多變量測試 (MVT)：同時測試多個頁面元素（如標題、圖片、按鈕顏色）的不同組合，找出最佳的元素組合。
MVT 需要更大的流量來獲得統計顯著的結果，因為需要測試的組合數量更多。
#15
★★★★
統計學習 (Statistical Learning) 概觀
定義
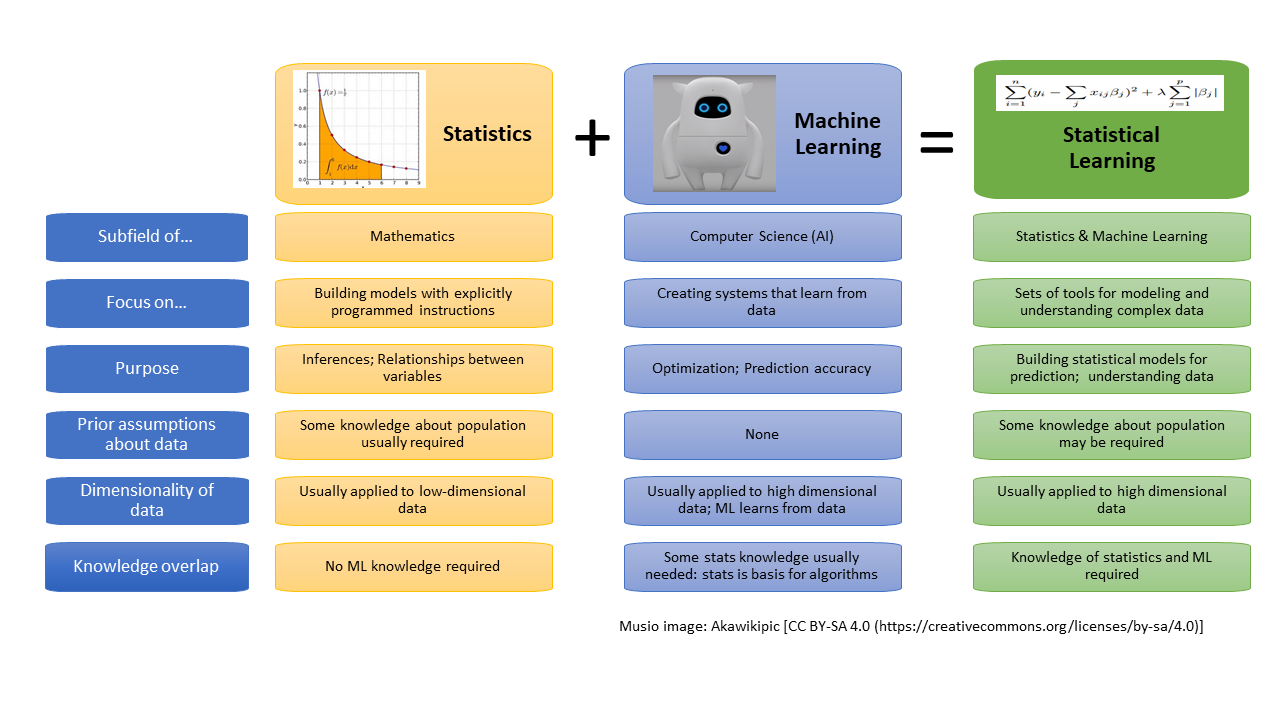
統計學習是一套基於數據來理解現象、建立模型、進行預測的工具和方法。它與機器學習密切相關，但更強調模型的統計性質、可解釋性和不確定性評估。
  • 目標：估計一個函數 f，使得 Y ≈ f(X)，其中 X 是輸入變數（特徵），Y 是輸出變數（反應）。
  • 主要任務：預測 (Prediction) 和推論 (Inference)。
#16
★★★★
監督式學習 (Supervised Learning) vs 非監督式學習 (Unsupervised Learning)
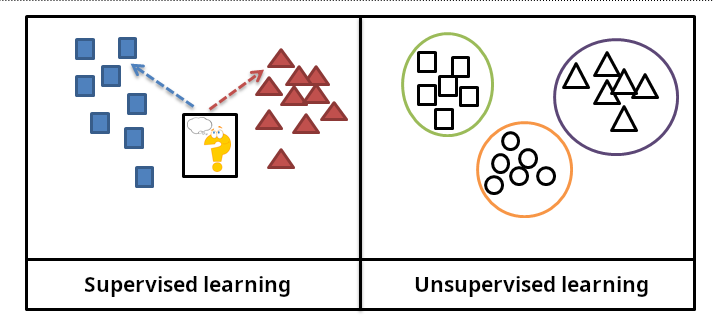
統計學習分類
  • 監督式學習：有標籤的數據，即每個輸入 X 都有對應的輸出 Y。目標是學習從 X 到 Y 的映射關係 f。
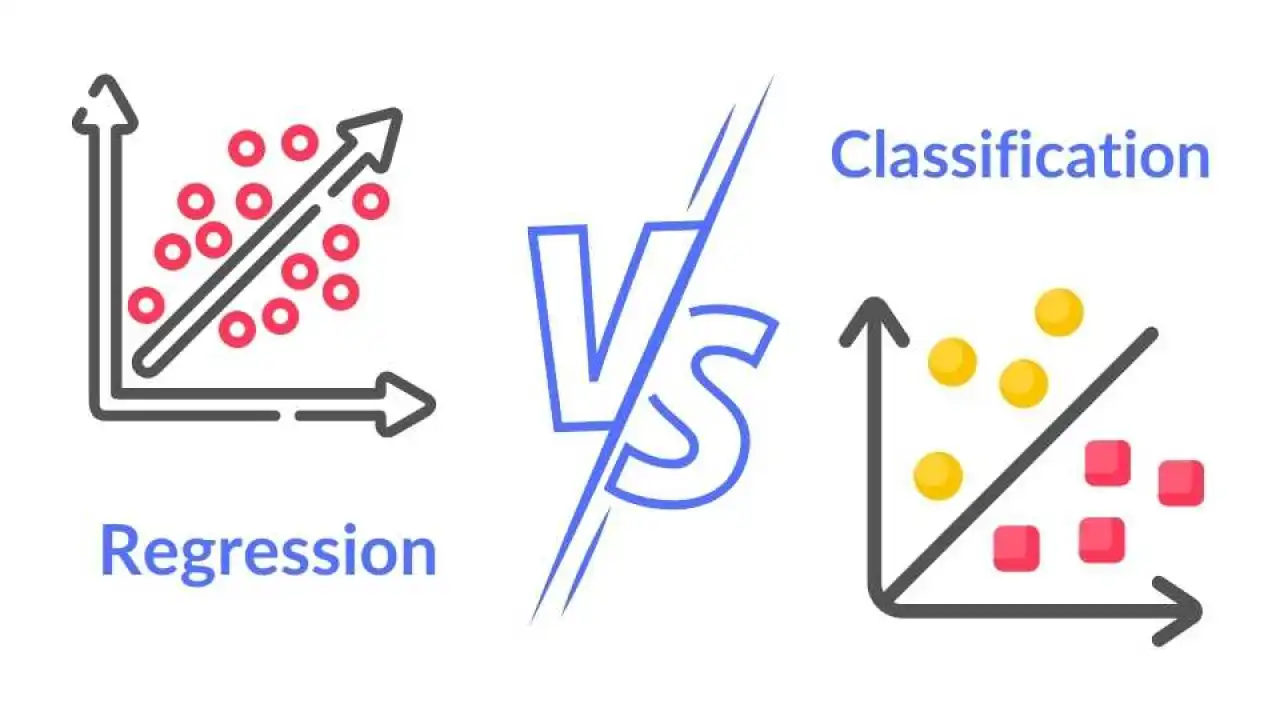
    • 回歸 (Regression)：預測連續型輸出 Y (如房價、銷售額)。Q8 提到了線性回歸用於預測。
    • 分類 (Classification)：預測類別型輸出 Y (如垃圾郵件/非垃圾郵件、客戶流失/不流失)。
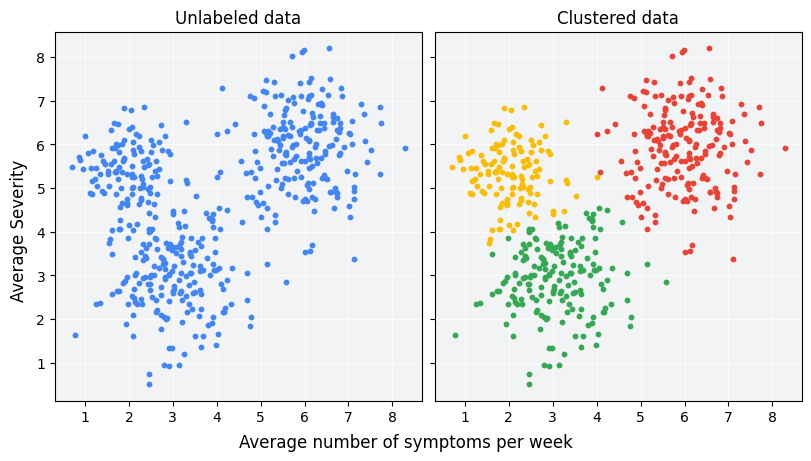
  • 非監督式學習：沒有標籤的數據，只有輸入 X。目標是發現數據中的結構或模式。
    • 分群 (Clustering)：將相似的數據點分到同一群組。Q5 提到了 K-means 分群。
    • 降維 (Dimensionality Reduction)：如 PCA。
#17
★★★★★
模型評估與選擇 - 偏差-變異權衡 (Bias-Variance Trade-off)
核心概念
在監督式學習中，模型的預測誤差可以分解為偏差、變異和不可避免的誤差：
  • 偏差 (Bias)：模型預測值與真實值之間的系統性差異。高偏差（欠擬合, Underfitting）表示模型過於簡單，未能捕捉數據的真實模式。
  • 變異 (Variance)：模型預測對於不同訓練數據集的敏感度。高變異（過擬合, Overfitting）表示模型過於複雜，對訓練數據的雜訊過度反應，導致在新數據上表現不佳。
  • 權衡：通常，增加模型複雜度會降低偏差但增加變異，反之亦然。目標是找到偏差和變異之間的最佳平衡點，以最小化總體預測誤差。
Q3 提到了降低過擬合的方法（增加正則化項）。
#18
★★★★
模型評估方法 - 交叉驗證 (Cross-Validation)
目的與方法
交叉驗證是一種評估模型在未見數據上表現（泛化能力）的技術，並有助於調整模型超參數和避免過擬合。
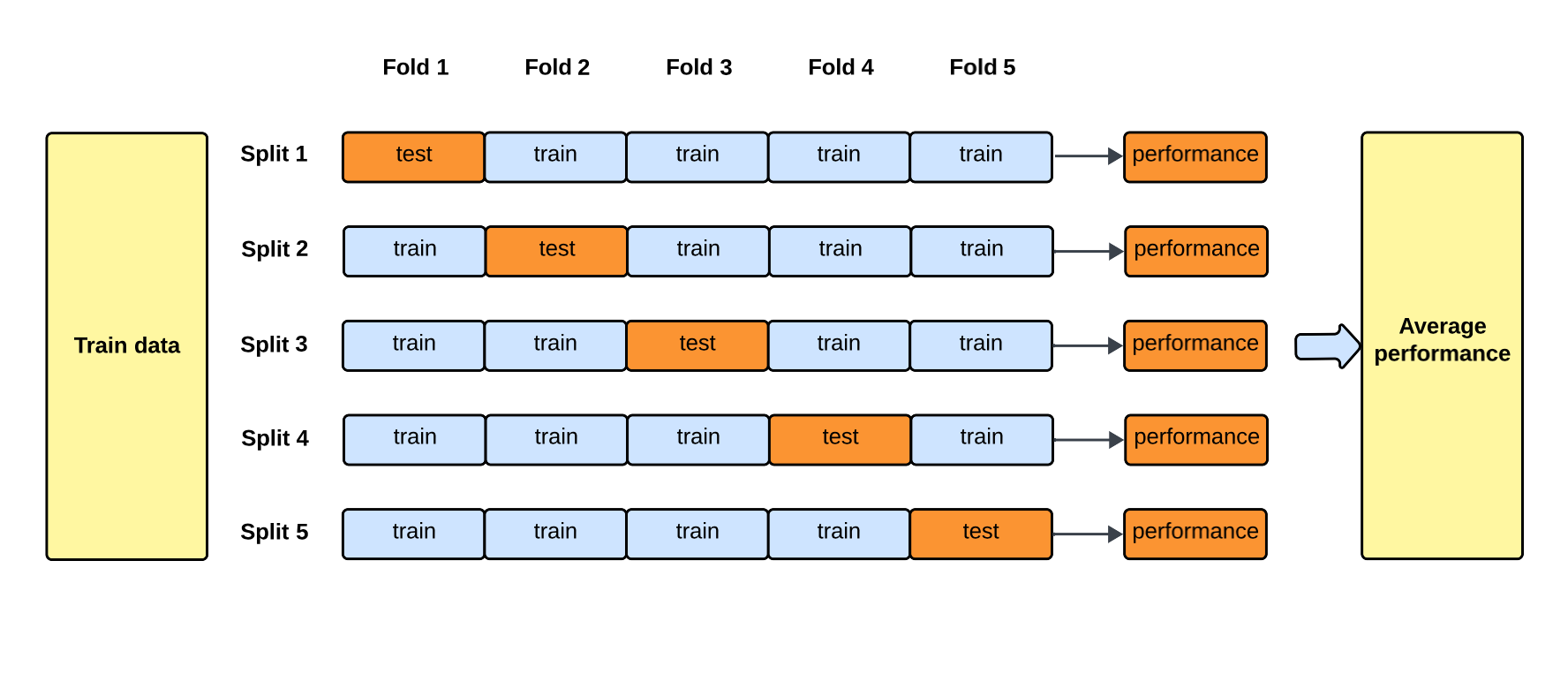
  • k 折交叉驗證 (k-fold Cross-Validation)：將數據隨機分成 k 個子集（折）。輪流將其中 k-1 折作為訓練集，剩下 1 折作為驗證集，重複 k 次。最後將 k 次的評估指標（如誤差率）平均，作為模型的最終評估。
  • 優點：比簡單地劃分訓練/測試集更有效地利用數據，評估結果更穩健。
Q9 考察了交叉驗證的主要目的。
#19
★★★★
分散式計算框架 (Distributed Computing Frameworks) - MapReduce & Spark
基本概念
為了處理無法在單機上完成的大數據統計計算，需要分散式計算框架：
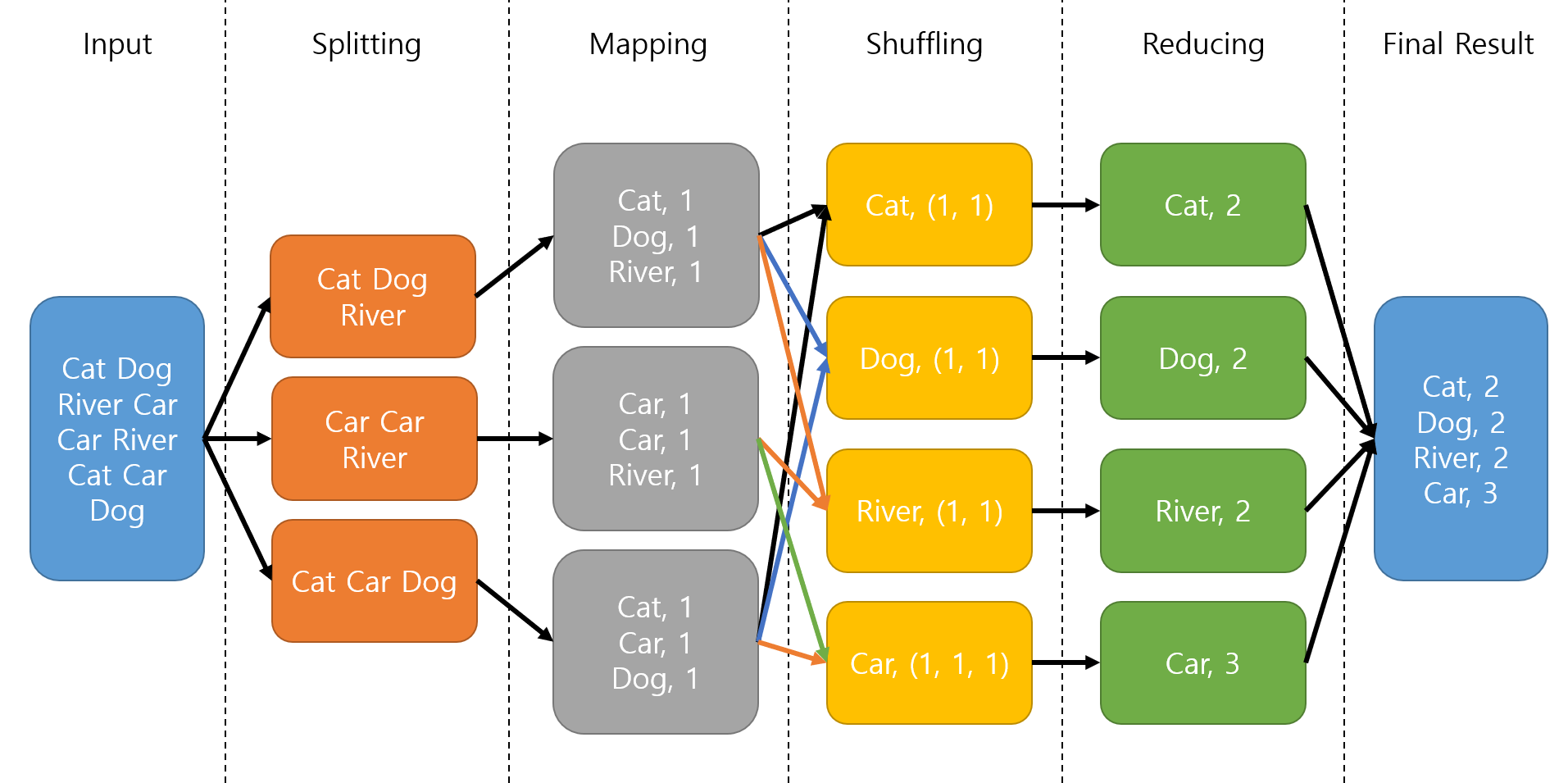
  • MapReduce：一種編程模型和處理框架，用於在大型叢集上進行並行、分散式的數據處理。包含 Map（處理和轉換數據）和 Reduce（聚合結果）兩個主要階段。Q11 提到了 MapReduce。
  • Apache Spark：一個更快速、更通用的分散式計算引擎。它將數據載入記憶體（透過 RDD - Resilient Distributed Datasets 或 DataFrames）進行處理，比基於磁碟的 MapReduce 效能更好，支援迭代計算和互動式查詢，並提供 SQL、流處理、機器學習 (MLlib) 和圖計算函式庫。
#20
★★★
分散式環境下的統計挑戰
額外考量
在分散式環境中應用統計方法需要額外考量：
  • 通訊成本 (Communication Cost)：節點間數據傳輸可能成為瓶頸。
  • 演算法的並行化 (Parallelization)：如何將統計計算分解到多個節點並行執行。
  • 結果聚合 (Aggregation)：如何有效地合併各節點的計算結果。
  • 容錯性 (Fault Tolerance)：如何處理部分節點的故障。
許多統計方法需要重新設計或調整以適應分散式環境。
#21
★★★★
大數據視覺化 (Big Data Visualization) 的挑戰與策略
應對方法
將大數據視覺化面臨挑戰（數據量大、維度高、速度快），需要特殊策略：
  • 數據聚合/摘要 (Aggregation/Summarization)：不直接繪製所有點，而是繪製摘要統計量（如直方圖、盒鬚圖、熱力圖）。
  • 抽樣 (Sampling)：在數據子集上進行視覺化以觀察模式。
  • 降維 (Dimensionality Reduction)：將高維數據降到二維或三維進行視覺化（如使用 PCA, t-SNE）。
  • 互動式視覺化 (Interactive Visualization)：允許使用者縮放、篩選、鑽取數據以探索不同層級的細節。
  • 平行座標圖 (Parallel Coordinates Plot)：用於視覺化多維數據。
#22
★★★★★
統計學在機器學習生命週期中的作用
整合應用
統計學在機器學習的各個階段都扮演重要角色：
  • 數據探索與理解：使用敘述統計和視覺化來理解數據特性。
  • 特徵工程：降維 (PCA)、檢驗變數相關性。
  • 模型建立：許多機器學習模型本身就基於統計原理（如線性回歸、羅吉斯回歸、貝氏分類器）。
  • 模型評估：使用假設檢定比較模型效能（如比較兩種模型的準確率是否有顯著差異）、計算信賴區間評估預測不確定性。
  • 結果解釋：解釋模型的預測和變數的重要性。
沒有找到符合條件的重點。
↑