iPAS AI應用規劃師 考試重點

L22103 假設檢定與統計推論
主題分類
1
假設檢定基礎概念
2
虛無假設與對立假設
3
檢定統計量、p值與顯著水準
4
型一錯誤與型二錯誤
5
檢定流程與決策
6
常用假設檢定(參數檢定)
7
常用假設檢定(無母數檢定)
8
統計推論與信賴區間
#1
★★★★★
假設檢定 (Hypothesis Testing) - 定義與目的
核心概念
假設檢定是一種統計推論 (Statistical Inference) 的方法，用於根據樣本資料來判斷關於母體參數（如平均數、比例、變異數）或母體分佈的某個假設是否成立。
  • 目的：利用樣本證據，對關於母體的陳述（假設）做出決策，判斷該陳述是否有足夠的證據支持或反對。
  • 例如：檢定新藥是否比舊藥更有效、檢定兩種教學方法的效果是否有差異。
#2
★★★★★
虛無假設 (Null Hypothesis, H₀)
定義與特性
虛無假設是研究者想要推翻或檢驗其真實性的假設，通常代表「沒有效果」、「沒有差異」或「現狀」的陳述。
  • 它是一個關於母體參數的明確陳述，包含等號（=, ≤, ≥）。
  • 檢定過程一開始假設 H₀ 為真，然後收集證據看是否能拒絕它。
  • 例如：H₀: 新藥效果 = 舊藥效果 (μ_new = μ_old)； H₀: 男性平均身高 ≤ 女性平均身高 (μ_male ≤ μ_female)。
#3
★★★★★
對立假設 (Alternative Hypothesis, H₁ 或 Ha)
定義與特性
對立假設是與虛無假設相對立的陳述，是研究者通常希望找到證據支持的假設。它代表了「有效果」、「有差異」或與現狀不同的情況。
  • 它通常不包含等號，而是使用 ≠, <, >。
  • H₀ 和 H₁ 是互斥且窮盡的，涵蓋了所有可能性。
  • 例如：H₁: 新藥效果 ≠ 舊藥效果 (μ_new ≠ μ_old)； H₁: 男性平均身高 > 女性平均身高 (μ_male > μ_female)。
  • 根據 H₁ 的形式，檢定可以是雙尾 (Two-tailed) (≠)、左尾 (Left-tailed) (<) 或右尾 (Right-tailed) (>)。
#4
★★★★★
檢定統計量 (Test Statistic)
定義與目的
檢定統計量是一個根據樣本資料計算出的數值，用於衡量樣本證據與虛無假設 H₀ 之間的不一致程度。
  • 其計算方式取決於檢定的類型（如 t 檢定、Z 檢定、卡方檢定）和檢定的參數。
  • 檢定統計量的值越大（或越小，取決於檢定類型和對立假設），表示樣本結果越偏離 H₀ 所預期的情況。
  • 例如：t 統計量、Z 統計量、χ² 統計量、F 統計量。
#5
★★★★★
p 值 (p-value)
定義與判讀
p 值是在假設虛無假設 H₀ 為真的前提下，觀察到當前樣本結果或更極端結果的機率。
  • 它衡量了樣本證據反對 H₀ 的強度。
  • p 值越小，表示觀察到的樣本結果在 H₀ 為真的情況下越不可能發生，反對 H₀ 的證據越強。
  • p 值不是 H₀ 為真的機率，也不是犯錯誤的機率。
  • 計算 p 值需要知道檢定統計量的值及其在 H₀ 下的抽樣分佈。
#6
★★★★★
顯著水準 (Significance Level, α)
定義與選擇
顯著水準 α 是在進行假設檢定前預先設定的一個閾值，代表研究者願意容忍犯型一錯誤（見後）的最大機率。
  • 它作為拒絕 H₀ 的決策標準。
  • 常用的 α 值包括 0.05 (5%)、0.01 (1%) 和 0.10 (10%)。
  • α 的選擇取決於研究領域的慣例和犯錯誤的後果嚴重性。α 越小，拒絕 H₀ 的標準越嚴格。
#7
★★★★★
型一錯誤 (Type I Error)
定義與機率
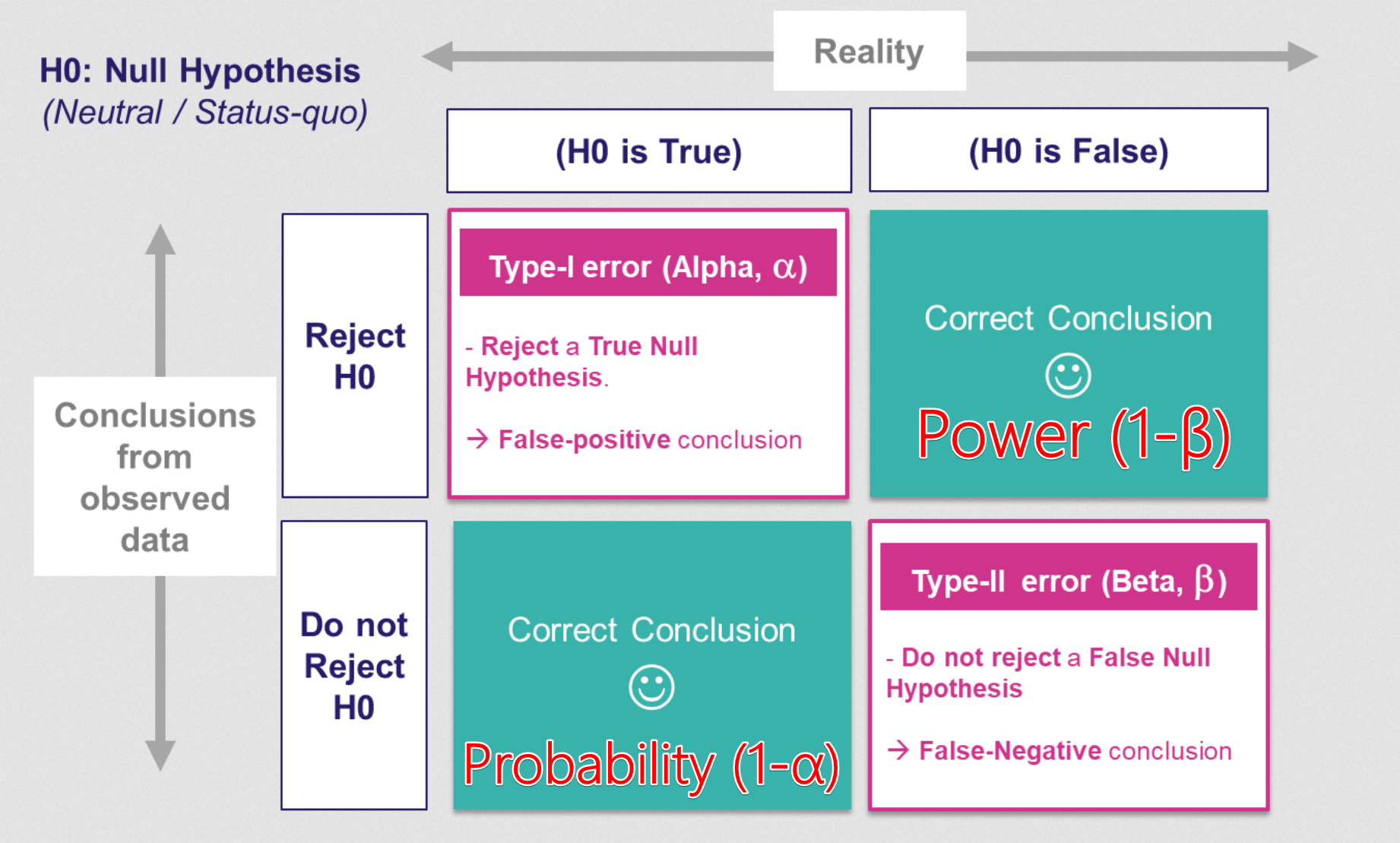
型一錯誤是指當虛無假設 H₀ 實際上為真時，我們卻錯誤地拒絕了 H₀。也稱為偽陽性 (False Positive)。
  • 犯型一錯誤的機率用 α 表示。
  • P(Type I Error) = P(拒絕 H₀ | H₀ 為真) = α。
  • 降低 α 可以減少犯型一錯誤的風險，但會增加犯型二錯誤的風險。
#8
★★★★★
型二錯誤 (Type II Error)
定義與機率
型二錯誤是指當虛無假設 H₀ 實際上為假（即對立假設 H₁ 為真）時，我們卻未能拒絕 H₀。也稱為偽陰性 (False Negative)。
  • 犯型二錯誤的機率用 β 表示。
  • P(Type II Error) = P(未能拒絕 H₀ | H₀ 為假) = β。
  • β 的大小受多種因素影響，包括 α、樣本大小、效應大小 (Effect Size) 和資料變異性。
#9
★★★★
統計檢定力 (Statistical Power)
定義與關係
統計檢定力是指當虛無假設 H₀ 實際上為假時，正確地拒絕 H₀ 的機率。
  • 檢定力 = 1 - β = P(拒絕 H₀ | H₀ 為假)。
  • 檢定力越高越好，表示研究越有可能偵測到真實存在的效應或差異。
  • 提高檢定力的方法：增加樣本大小、增大 α (不建議輕易做)、減小資料變異性、選擇效應量更大的研究設計。
#10
★★★★★
假設檢定的決策規則
p 值法
最常用的決策方法是比較 p 值與顯著水準 α：
  • 如果 p 值 ≤ α：拒絕虛無假設 H₀。表示觀察到的樣本結果足夠極端，足以反對 H₀。我們稱結果具有「統計顯著性」。
  • 如果 p 值 > α：未能拒絕 (Fail to Reject) 虛無假設 H₀。表示樣本證據不足以推翻 H₀。（注意：不是「接受 H₀」，因為檢定是基於 H₀ 為真的假設）。
#11
★★★★
假設檢定的基本流程
步驟
一個典型的假設檢定流程包含：
  1. 設定假設：明確定義虛無假設 H₀ 和對立假設 H₁。
  2. 選擇顯著水準 α。
  3. 選擇合適的檢定方法並計算檢定統計量。
  4. 確定拒絕域 (Rejection Region) 或計算 p 值。
  5. 做出決策：比較檢定統計量與臨界值，或比較 p 值與 α，決定是否拒絕 H₀。
  6. 解釋結果：根據決策，結合研究背景解釋結論。
#12
★★★★★
t 檢定 (t-test) - 適用情境
主要用途
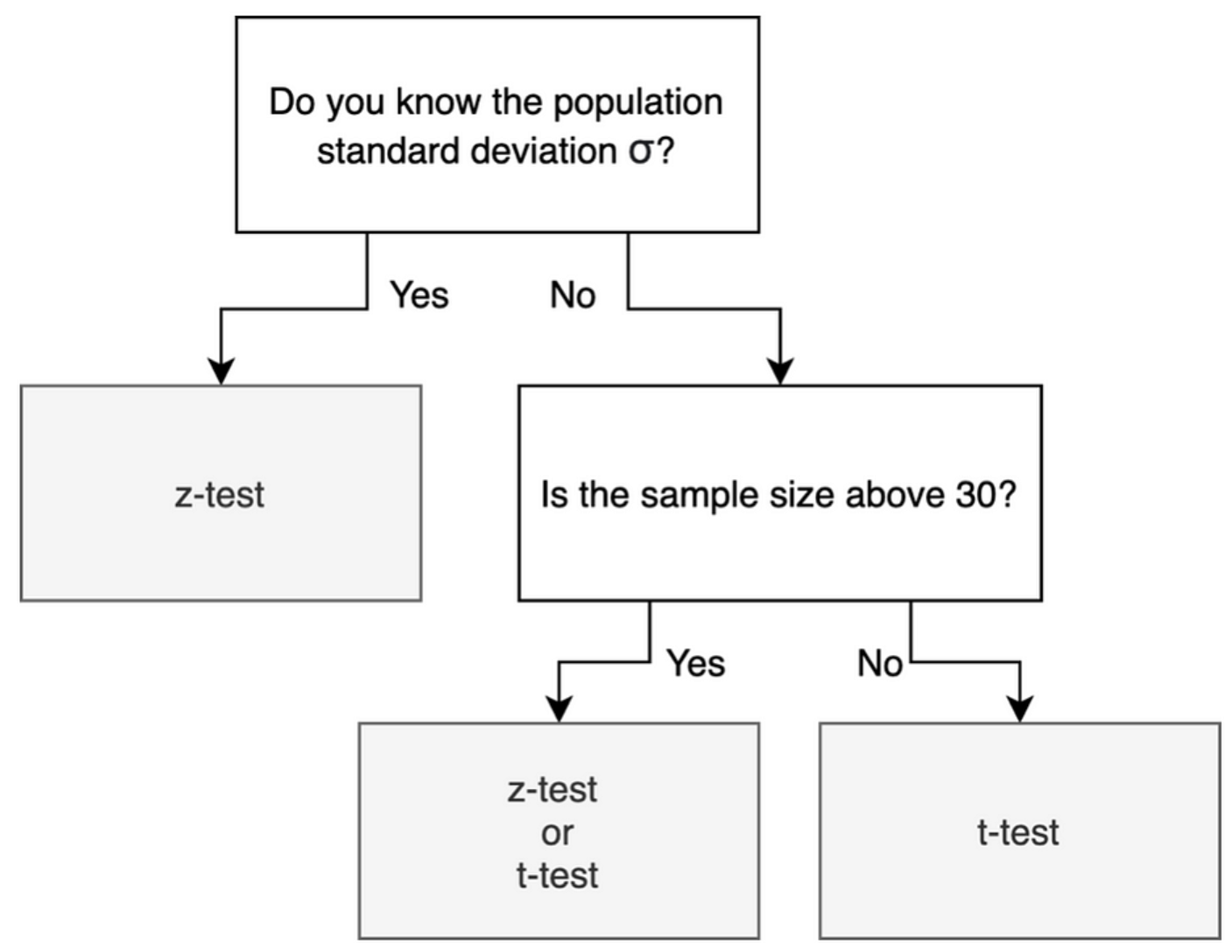
t 檢定主要用於檢定一個或兩個樣本平均數的假設。前提假設是資料來自常態分佈（或樣本數足夠大時依賴中央極限定理），且母體變異數未知（使用樣本變異數估計）。
  • 單樣本 t 檢定 (One-sample t-test)：檢定單個樣本的平均數是否等於一個已知的特定值。
  • 獨立樣本 t 檢定 (Independent samples t-test)：比較兩個獨立組別的平均數是否有顯著差異。
  • 成對樣本 t 檢定 (Paired samples t-test)：比較同一個體或配對個體在兩種不同處理或時間點下的平均數差異（檢定差值的平均數是否為 0）。
Q6(A) 和 Q6(B) 提到了 t 檢定的應用場景。
#13
★★★★
Z 檢定 (Z-test) - 適用情境
主要用途
Z 檢定也用於檢定一個或兩個樣本平均數（或比例）的假設，但其適用條件與 t 檢定略有不同：
  • 當母體變異數已知時，用於檢定平均數。
  • 當樣本數非常大（通常 n > 30 或更大）時，即使母體變異數未知，樣本標準差也能很好地估計母體標準差，此時 t 分佈趨近於 Z 分佈，也可以使用 Z 檢定（依賴中央極限定理）。
  • 常用於檢定樣本比例是否等於某特定值，或比較兩個樣本比例是否有差異（大樣本情況下）。
#14
★★★★
卡方檢定 (Chi-squared Test, χ² Test)
主要用途
卡方檢定主要用於分析類別型資料。
  • 適合度檢定 (Goodness-of-Fit Test)：檢定單個類別變數的觀察頻率分佈是否符合某個預期的理論分佈。
  • 獨立性檢定 (Test of Independence)：檢定兩個類別變數之間是否相互獨立（即是否有關聯）。基於列聯表 (Contingency Table)。
  • 同質性檢定 (Test of Homogeneity)：檢定多個不同母體（組別）在某個類別變數上的分佈比例是否相同。
Q6(D) 提到卡方檢定不適用於檢定平均數是否等於特定值。
#15
★★★★★
變異數分析 (Analysis of Variance, ANOVA) / F 檢定 (F-test)
主要用途
ANOVA 使用 F 檢定 來比較三個或以上獨立組別的平均數是否有顯著差異。
  • 基本思想：比較組間變異 (Between-group variance) 與組內變異 (Within-group variance)。如果組間變異遠大於組內變異，則傾向於認為各組平均數不全相等。
  • H₀：所有組別的母體平均數相等 (μ₁ = μ₂ = ... = μk)。
  • H₁：至少有兩組的母體平均數不相等。
  • 前提假設：各組資料來自常態分佈、各組變異數相等（變異數同質性）、樣本獨立。
Q6(C) 提到了 F 檢定（ANOVA）適用於比較多個組別（如三個年級）的平均身高差異。 F 檢定也可用於比較兩個母體的變異數。
#16
★★★★
信賴區間 (Confidence Interval, CI)
定義與意義
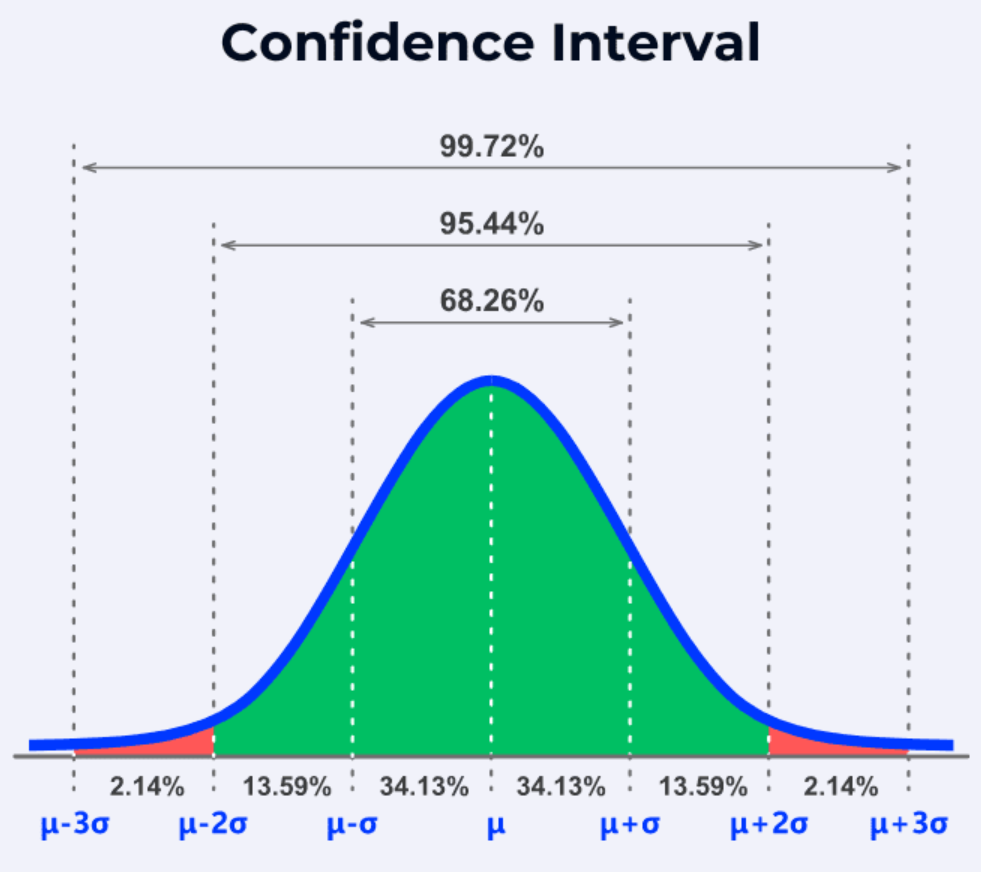
信賴區間是統計推論的一種形式，提供了一個根據樣本資料估計出的區間，我們有一定信心（信賴水準）認為真實的母體參數（如平均數 μ 或比例 p）會落入這個區間內。
  • 例如，一個 95% 信賴區間表示：如果我們重複抽樣並建構區間多次，約有 95% 的區間會包含真實的母體參數。
  • 信賴水準 (Confidence Level)：通常設為 90%、95% 或 99%。信賴水準越高，區間越寬。
  • 區間寬度受信賴水準、樣本大小和資料變異性影響。樣本越大、變異性越小，區間越窄（估計越精確）。
#17
★★★
點估計 (Point Estimation) vs 區間估計 (Interval Estimation)
比較
都是用樣本資訊來推論母體參數：
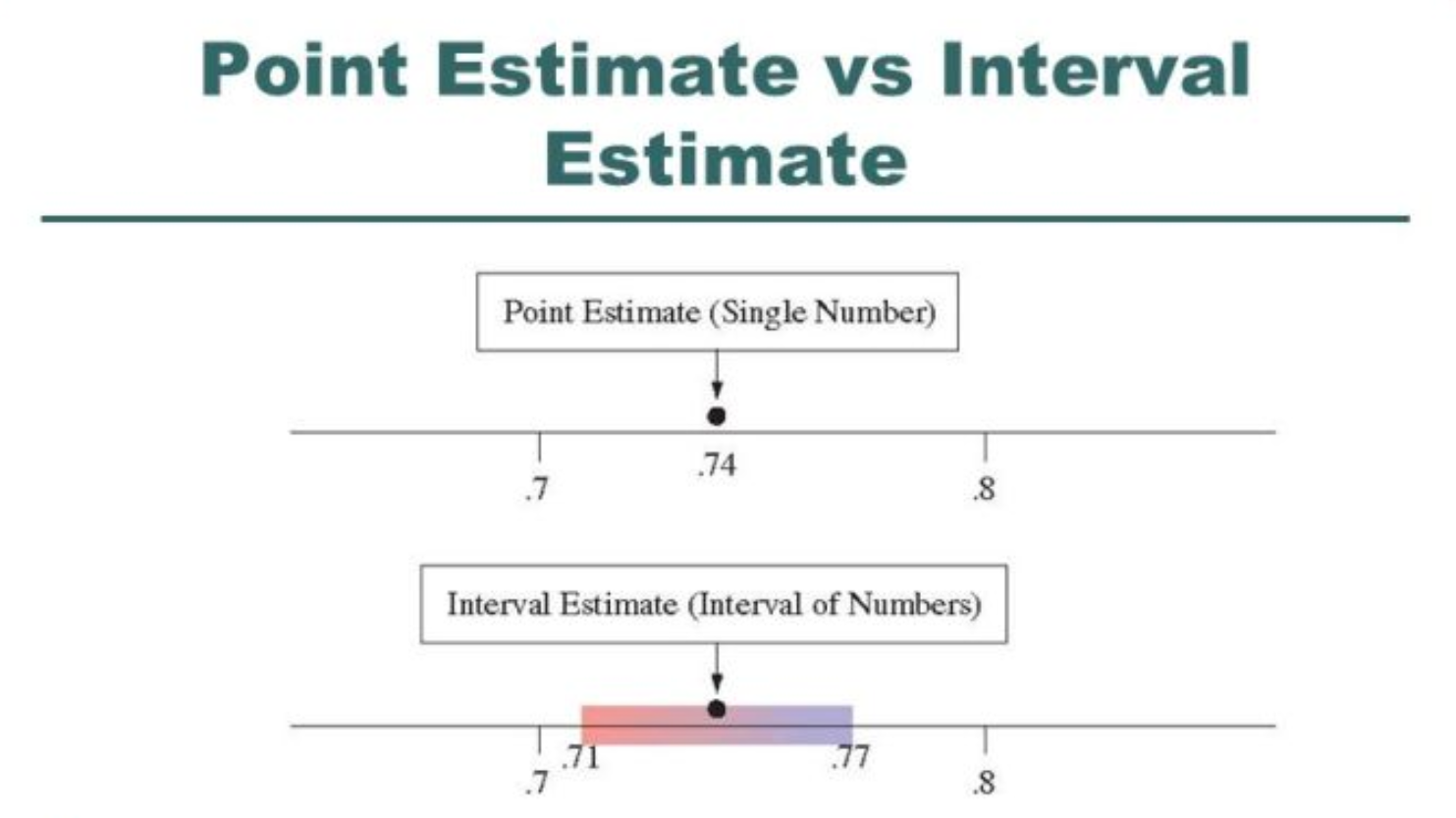
  • 點估計：用單一數值（如樣本平均數 x̄）來估計母體參數（如 μ）。簡單直觀，但無法提供估計的精確度或信賴程度。
  • 區間估計：提供一個可能包含母體參數的區間（信賴區間），並附帶一個信賴水準，反映了估計的不確定性。
#18
★★★
參數檢定 (Parametric Test) vs 無母數檢定 (Nonparametric Test)
區別
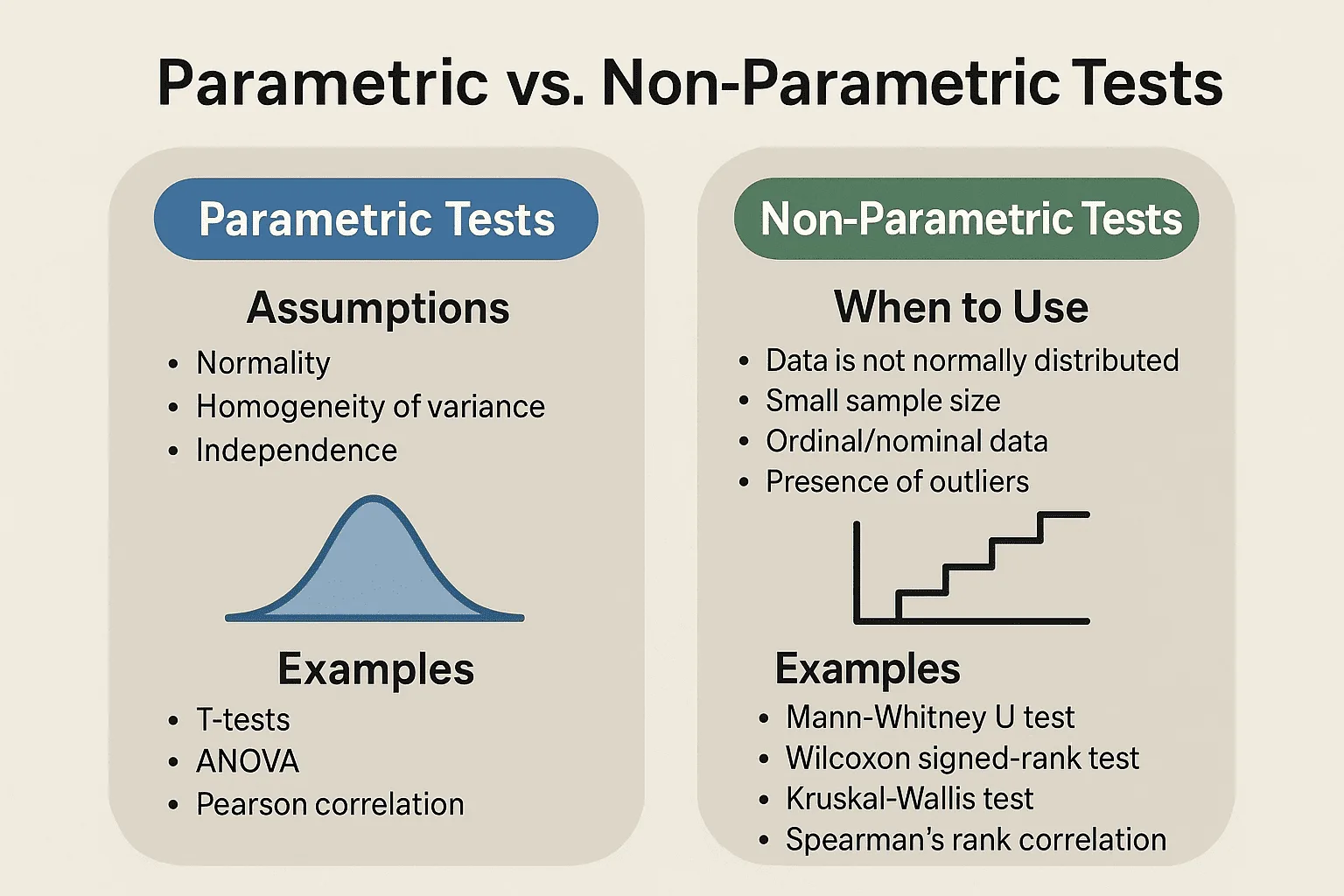
  • 參數檢定：對母體分佈有特定假設（通常是常態分佈），且檢定的是關於母體參數（如平均數、變異數）的假設。例如：t 檢定、Z 檢定、ANOVA。
  • 無母數檢定：對母體分佈沒有嚴格的假設（或假設較少），適用於分佈未知或非常態、小樣本、或次序型/名目型資料。檢定的假設通常與參數無關（如中位數、分佈形狀）。例如：卡方檢定、符號檢定、等級和檢定。
通常在滿足假設條件下，參數檢定比無母數檢定有更高的統計檢定力。
#19
★★
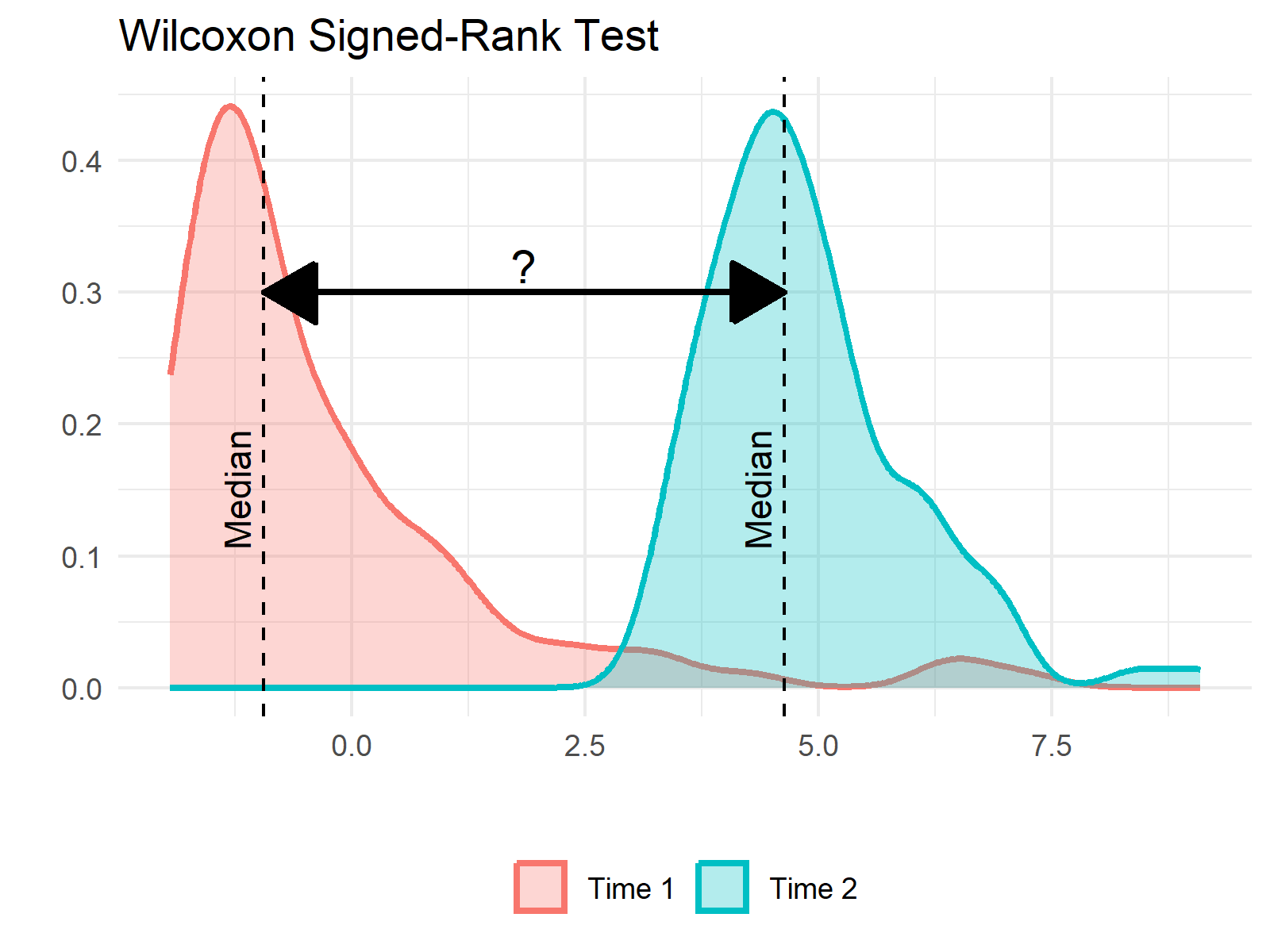
魏克森符號等級檢定 (Wilcoxon Signed-Rank Test)
用途
魏克森符號等級檢定是成對樣本 t 檢定的無母數替代方法。
  • 用於比較兩個相關樣本或重複測量的中位數差異，當資料不符合常態分佈假設時使用。
  • 它考慮了配對差異的符號和等級。
#20
★★
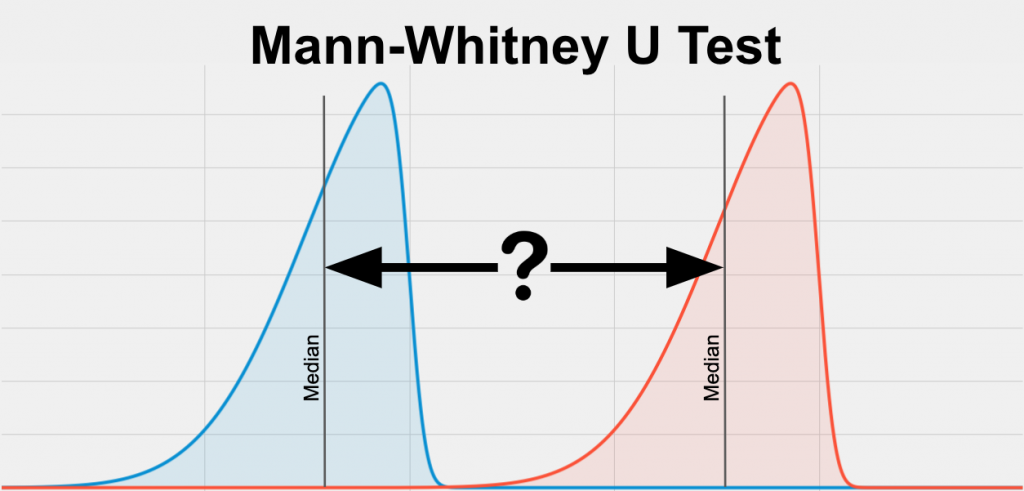
曼-惠特尼 U 檢定 (Mann-Whitney U Test / Wilcoxon Rank-Sum Test)
用途
曼-惠特尼 U 檢定是獨立樣本 t 檢定的無母數替代方法。
  • 用於比較兩個獨立樣本的中位數（或更準確地說是分佈位置）是否有差異，當資料不符合常態分佈假設時使用。
  • 它基於兩個樣本混合後的等級和。
#21
★★
克魯斯卡-瓦利斯檢定 (Kruskal-Wallis Test)
用途
克魯斯卡-瓦利斯檢定是單因子 ANOVA 的無母數替代方法。
  • 用於比較三個或以上獨立樣本的中位數（或分佈位置）是否有差異，當資料不符合常態分佈或變異數同質性假設時使用。
  • 它基於所有樣本混合後的等級和。
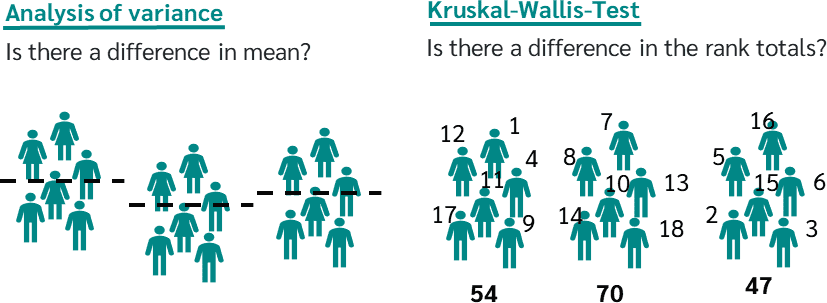
#22
★★★
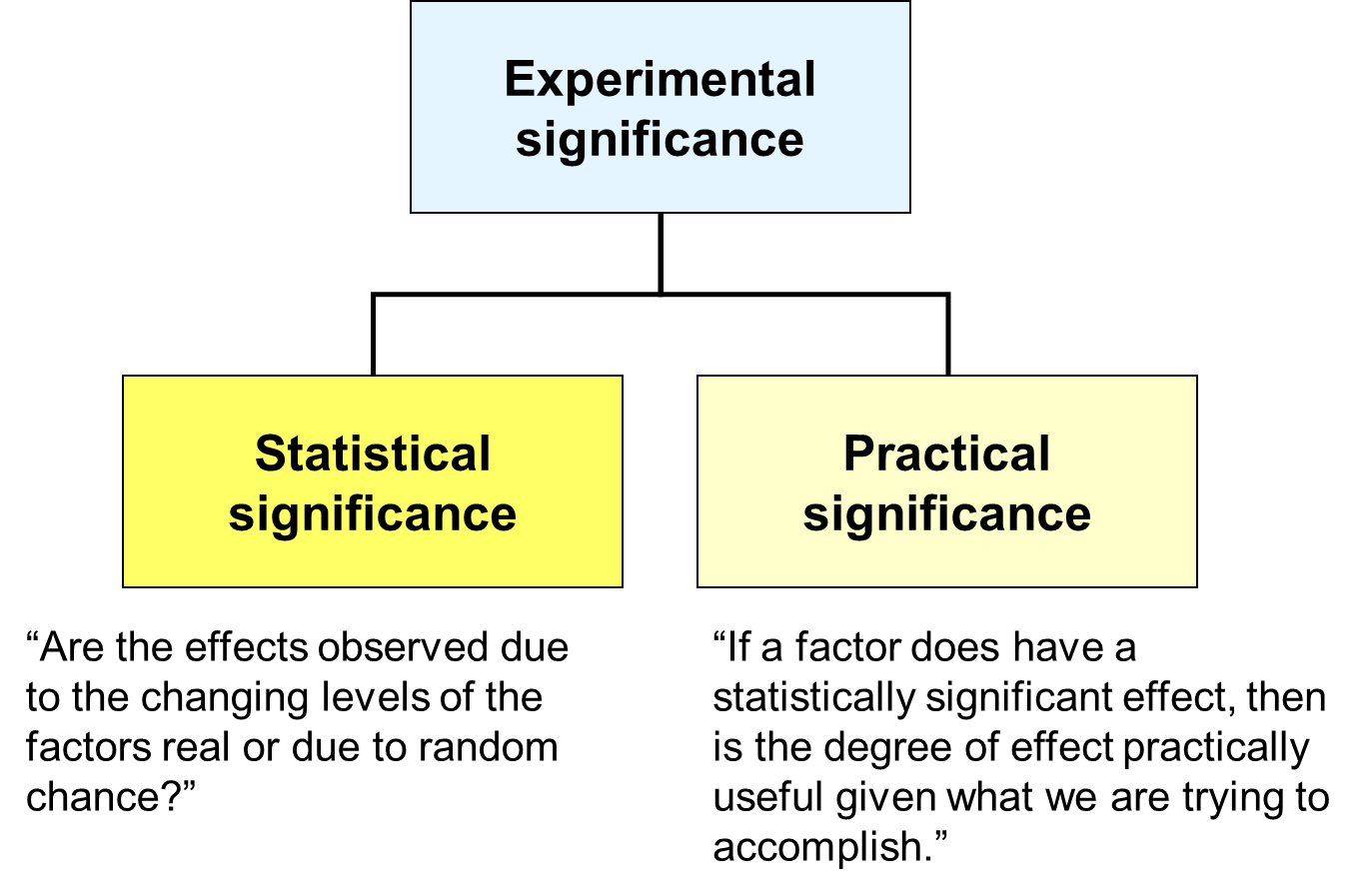
統計顯著性 (Statistical Significance) vs 實際顯著性 (Practical Significance)
區別
  • 統計顯著性：指觀察到的結果（如樣本平均數差異）不太可能僅由隨機抽樣誤差引起（通常指 p ≤ α）。
  • 實際顯著性：指觀察到的效應或差異在現實世界中是否具有重要性或實用價值。
非常大的樣本量可能導致微小的、實際意義不大的差異也達到統計顯著性。因此，除了 p 值，還應考慮效應大小 (Effect Size) 和信賴區間來評估結果的實際意義。
#23
★★
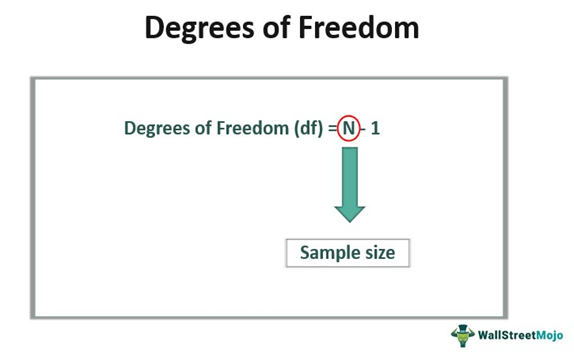
自由度 (Degrees of Freedom, df)
概念
自由度是指在計算統計量時，可以自由變化的數值的個數。
  • 它影響 t 分佈、卡方分佈、F 分佈等抽樣分佈的形狀。
  • 例如，在計算樣本變異數時，由於使用了樣本平均數（一個由樣本資料決定的值），自由度為 n-1。在獨立樣本 t 檢定中，自由度通常與兩個樣本的大小有關。
#24
★★★
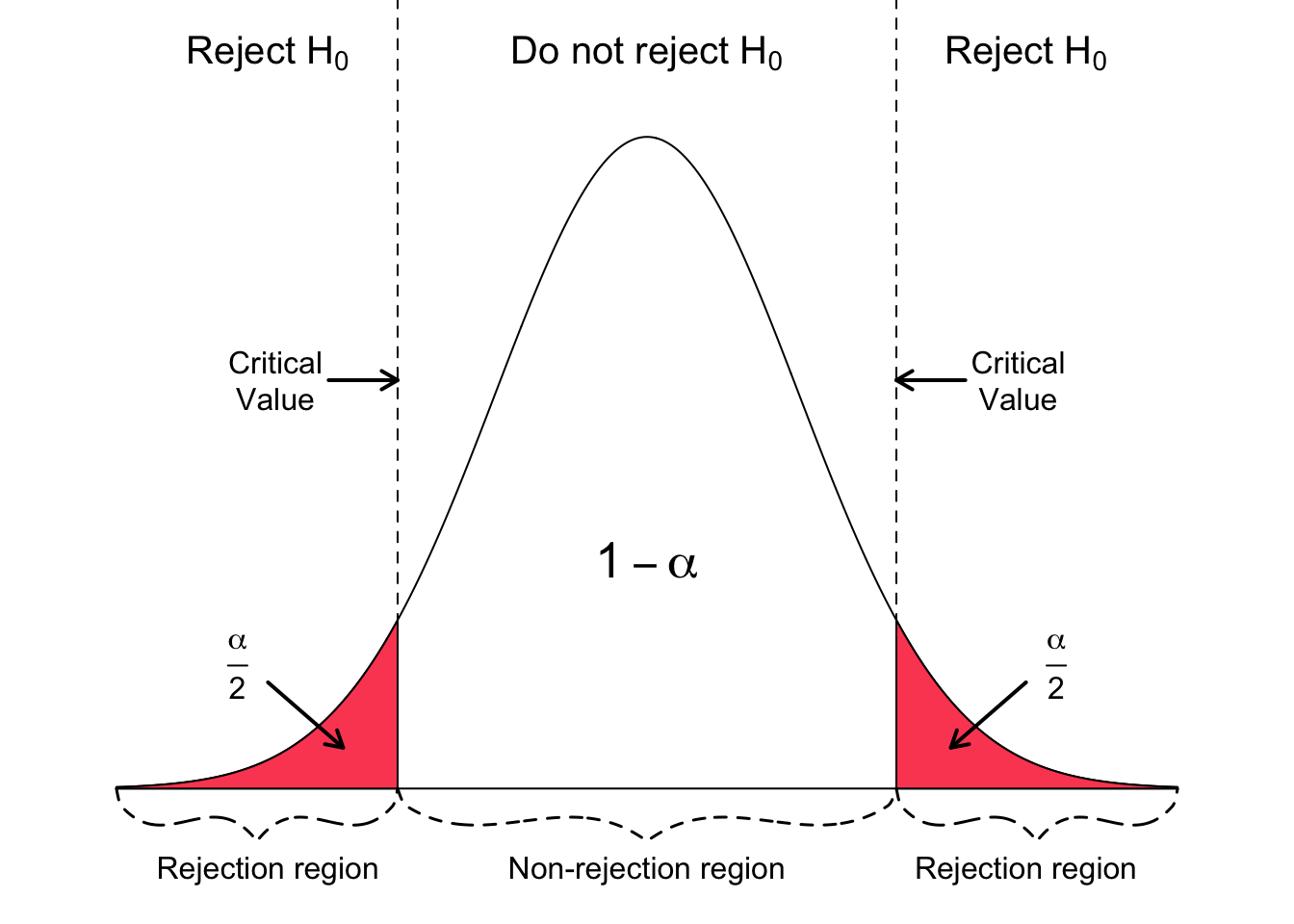
臨界值 (Critical Value)
定義與用途
臨界值是在假設檢定中，根據顯著水準 α 和檢定統計量的分佈（如 t 分佈、Z 分佈）確定的閾值。
  • 它定義了拒絕域的邊界。
  • 臨界值法決策規則：如果計算出的檢定統計量的值落入拒絕域（即比臨界值更極端），則拒絕 H₀。
  • 在 p 值法普及後，臨界值法相對少用，但理解其概念有助於理解檢定原理。
沒有找到符合條件的重點。
↑