iPAS AI應用規劃師經典題庫

#1

★★★★

根據機率的公理化定義，下列關於事件 A 的機率 P(A) 的敘述何者恆為真？

A

P(A) 可以是負數

B

0 ≤ P(A) ≤ 1

C

P(A) 必定大於 1

D

P(A) 必定等於 0.5

答案解析

機率公理（Axioms of Probability）是機率論的基礎，由科摩哥洛夫（Kolmogorov）提出。主要包含三條公理：

非負性（Non-negativity）：對於任何事件 A，其機率 P(A) ≥ 0。
歸一性（Normalization）：樣本空間 S（包含所有可能結果的集合）的機率 P(S) = 1。
可加性（Additivity）：對於一系列互斥（Mutually Exclusive）事件 A1, A2, ...，這些事件聯集的機率等於它們各自機率的總和。

根據公理 1 和公理 2（以及事件 A 是樣本空間 S 的子集），可以推導出任何事件 A 的機率必定介於 0 和 1 之間，即 0 ≤ P(A) ≤ 1。選項 B 正確。選項 A 和 C 違反公理。選項 D 僅在特定情況下成立。

#2

★★★★★

一個離散隨機變數 X 的期望值（Expected Value）E[X] 代表什麼意義？

A

X 最常出現的數值

B

X 所有可能數值根據其發生機率加權的平均值，代表 X 的長期平均表現

C

X 的最大可能數值減去最小可能數值

D

X 的數值偏離其平均值的平均程度

答案解析

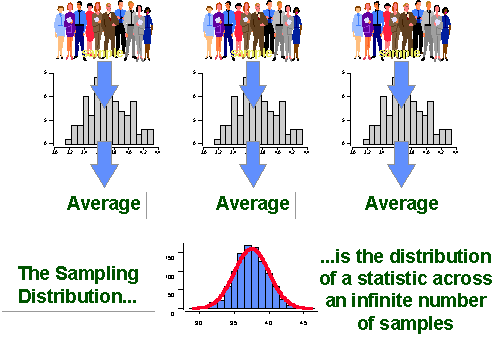
期望值是隨機變數的「中心」或「平均」的量度。對於一個離散隨機變數 X，其可能取值為 x1, x2, ..., xn，對應的機率為 P(X=x1), P(X=x2), ..., P(X=xn)。期望值 E[X] 的計算公式為：E[X] = Σ [xi * P(X=xi)]，即將每個可能值乘以其發生的機率，然後加總。它代表了如果我們重複進行這個隨機試驗很多次，觀察到的 X 值的長期平均結果會趨近於期望值。選項 A 是眾數（Mode）。選項 C 是全距（Range）。選項 D 描述的是變異數或標準差的概念。

#3

★★★★★

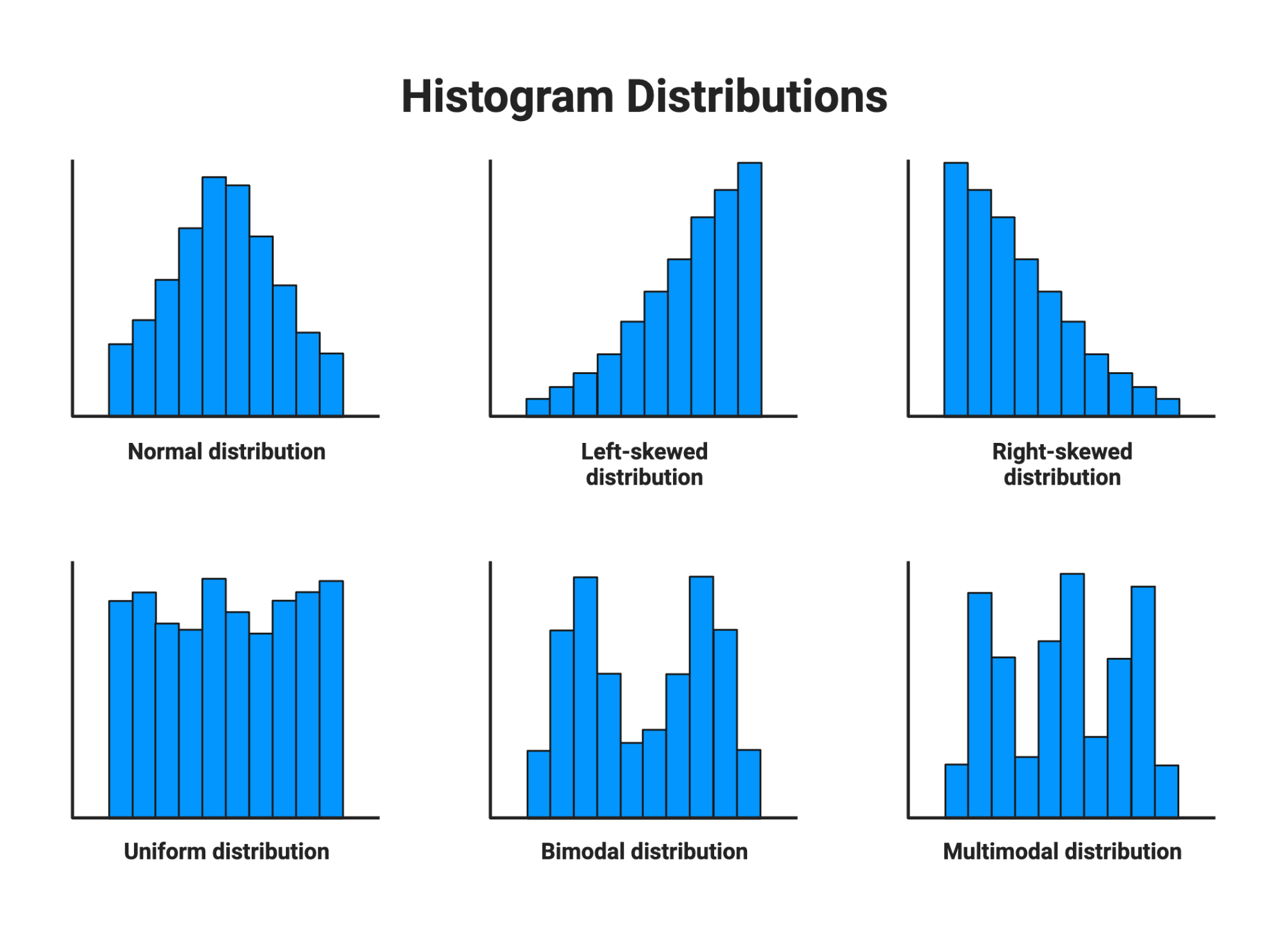
二項分佈（Binomial Distribution）描述的是下列哪種情境的機率？

A

在固定時間間隔或空間區域內，某事件發生的次數

B

進行 n 次獨立的伯努利試驗（Bernoulli Trial），每次試驗成功機率為 p，觀察到恰好 k 次成功的機率

C

連續型隨機變數落在某個特定區間的機率

D

直到第一次成功發生所需的試驗次數

答案解析

二項分佈用於模擬滿足以下條件的隨機試驗：

試驗由固定次數 n 的重複試驗組成。
每次試驗都是獨立的。
每次試驗只有兩種可能結果，通常稱為「成功」和「失敗」。
每次試驗成功的機率 p 保持不變（失敗機率則為 1-p）。

二項分佈計算的是在這 n 次試驗中，觀察到恰好 k 次成功的機率。選項 A 描述的是卜瓦松分佈（Poisson Distribution）的典型情境。選項 C 涉及連續分佈。選項 D 描述的是幾何分佈（Geometric Distribution）。

#4

★★★★★

常態分佈（Normal Distribution）的機率密度函數（Probability Density Function, PDF）曲線形狀主要由哪兩個參數決定？

A

試驗次數 n 和成功機率 p

B

平均數（Mean, μ）和標準差（Standard Deviation, σ）

C

事件發生率 λ

D

自由度（Degrees of Freedom）

答案解析

常態分佈是最重要的連續機率分佈之一，其機率密度函數呈現對稱的鐘形曲線。這個曲線的位置和形狀完全由兩個參數決定：

平均數 (μ)：決定了分佈的中心位置，即鐘形曲線對稱軸的位置。
標準差 (σ)：決定了分佈的離散程度或寬度。標準差越大，曲線越矮胖（數據越分散）；標準差越小，曲線越高瘦（數據越集中）。

選項 A 是二項分佈的參數。選項 C 是卜瓦松分佈或指數分佈的參數。選項 D 是 t 分佈或卡方分佈的參數。

#5

★★★★★

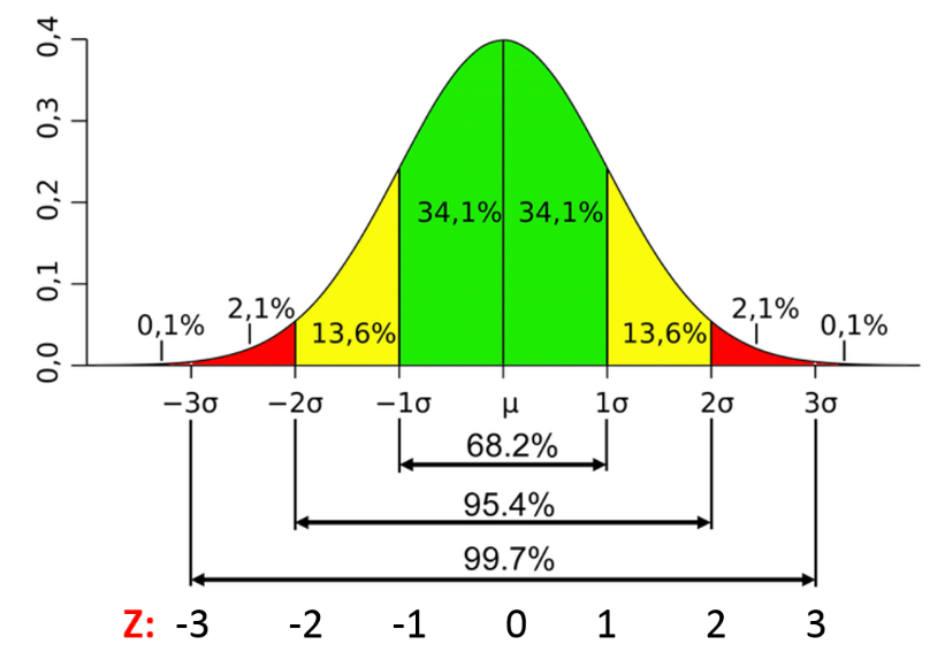
根據常態分佈的經驗法則（Empirical Rule），約有多少比例的數據會落在距離平均數 μ 正負一個標準差 σ 的範圍內（即 [μ - σ, μ + σ]）？

A

約 50%

B

約 68%

C

約 95%

D

約 99.7%

答案解析

經驗法則（也稱為 68-95-99.7 法則）是對常態分佈數據散佈情況的近似描述：

約 68% 的數據落在平均數正負一個標準差的範圍內 [μ - σ, μ + σ]。
約 95% 的數據落在平均數正負兩個標準差的範圍內 [μ - 2σ, μ + 2σ]。
約 99.7% 的數據落在平均數正負三個標準差的範圍内 [μ - 3σ, μ + 3σ]。

這個法則對於理解常態分佈數據的集中和離散情況非常有用。因此，落在 [μ - σ, μ + σ] 範圍內的數據約佔 68%。

#6

★★★★★

中央極限定理（Central Limit Theorem, CLT）的主要內容是關於什麼的分佈？

A

單個隨機樣本的分佈

B

從任何母體（無論其分佈如何）中抽取的大量獨立隨機樣本的樣本平均數（Sample Mean）的分佈

C

母體變異數（Population Variance）的分佈

D

單次伯努利試驗成功機率的分佈

答案解析

中央極限定理是統計學中一個非常重要的定理。它指出，如果從一個任何分佈（不一定需要是常態分佈）的母體中，重複抽取足夠大的獨立隨機樣本（通常認為樣本大小 n ≥ 30 即可），那麼這些樣本平均數的分佈將會近似於常態分佈。這個近似常態分佈的平均數等於母體平均數 μ，標準差（稱為標準誤 Standard Error, SE）等於母體標準差 σ 除以樣本大小的平方根（σ/√n）。CLT 的重要性在於它允許我們在不知道母體分佈的情況下，利用常態分佈來對樣本平均數進行統計推斷（如建立信賴區間、進行假設檢定）。

#7

★★★★

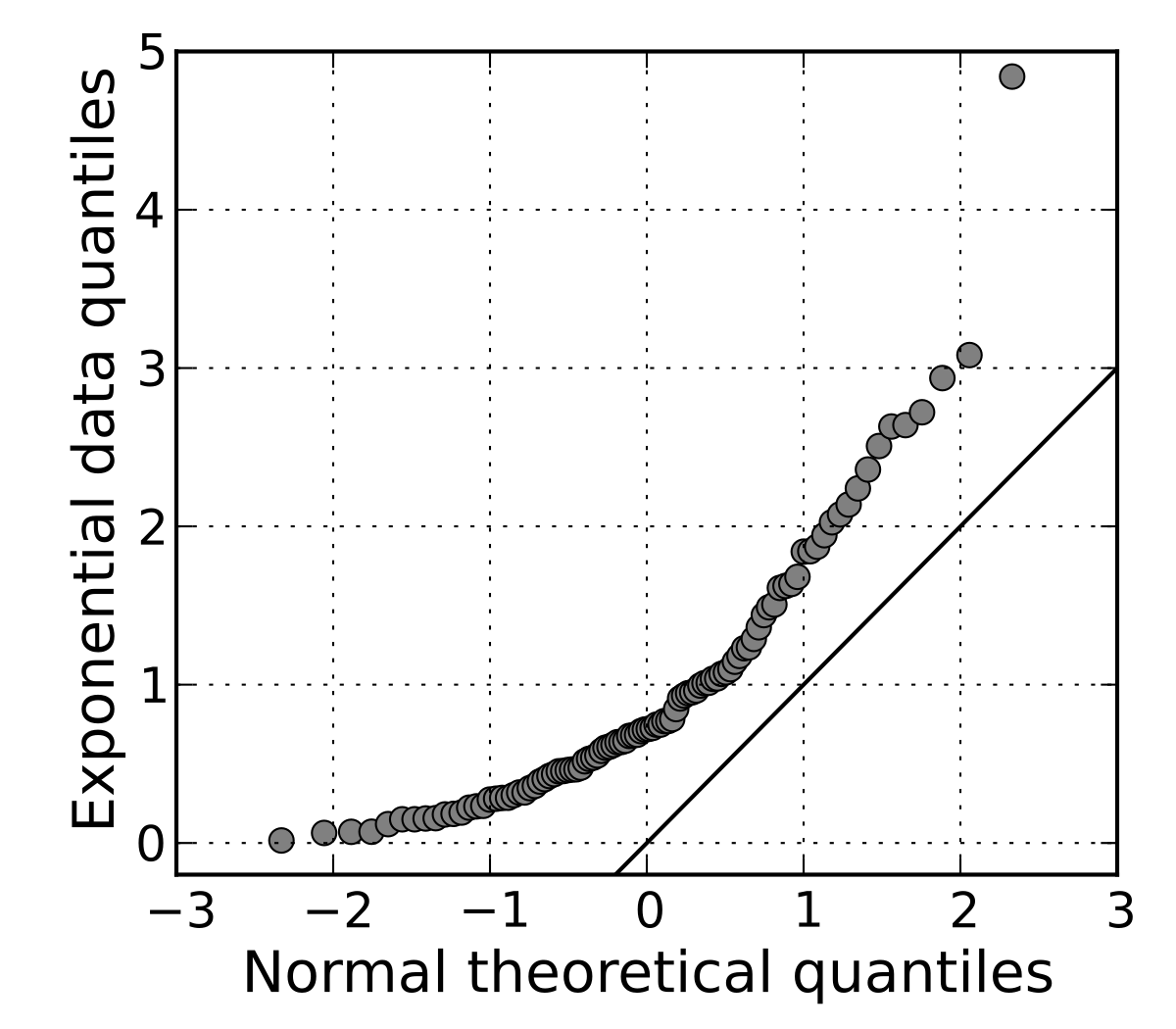
Q-Q 圖（Quantile-Quantile Plot）常用於檢查什麼？

A

兩個類別變數之間是否存在關聯

B

一組樣本數據的分佈是否接近於某個理論分佈（例如常態分佈）

C

數據中是否存在異常值

D

兩個數值變數之間的線性相關強度

答案解析

Q-Q 圖是一種視覺化比較兩組數據分佈或一組數據與理論分佈（最常用的是常態分佈）的圖形方法。它繪製的是兩組數據（或樣本數據與理論分佈）相對應的分位數（Quantiles）的散佈圖。如果樣本數據的分佈與比較的理論分佈非常吻合，那麼 Q-Q 圖上的點應該大致落在一條直線上（通常是 y=x 的對角線）。如果點明顯偏離直線，則表明樣本數據的分佈與理論分佈存在差異。Q-Q 圖是判斷數據是否服從常態分佈假設的常用視覺化工具。

#8

★★★★

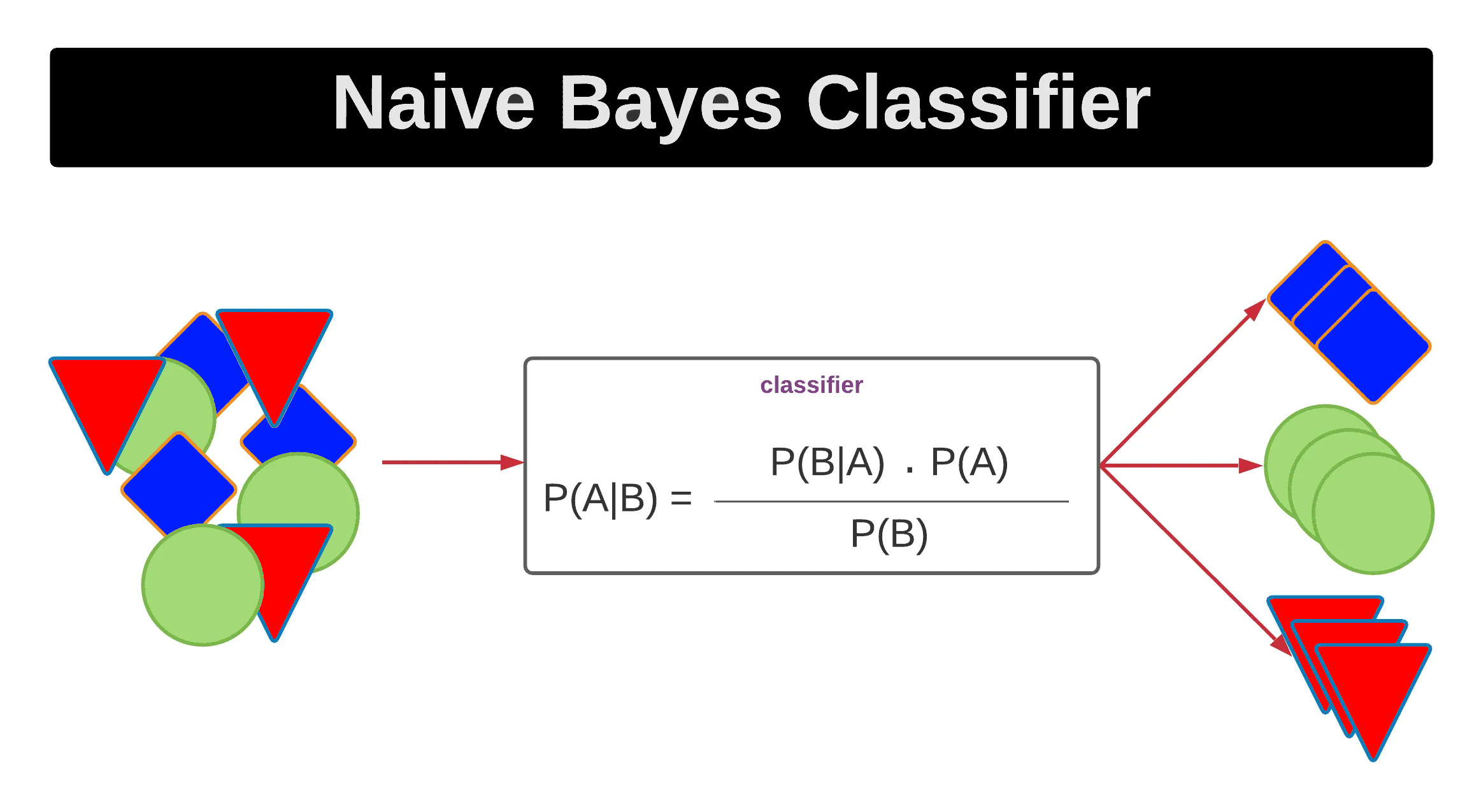
在機器學習的貝氏分類器（Naive Bayes Classifier）中，通常假設特徵之間是什麼關係，以簡化機率計算？

A

完全線性相關

B

在給定類別的條件下，特徵之間相互獨立（條件獨立性假設）

C

特徵之間存在複雜的非線性關係

D

所有特徵都服從常態分佈

答案解析

貝氏分類器是基於貝氏定理（Bayes' Theorem）的一類分類演算法。它計算給定特徵條件下，樣本屬於每個類別的後驗機率（Posterior Probability），並將樣本歸類到後驗機率最大的那個類別。「單純」（Naive）貝氏分類器的「單純」之處在於它做了一個很強的假設：假設所有特徵在給定類別的條件下是相互獨立的。這個條件獨立性假設大大簡化了聯合機率的計算，使得模型易於實現且計算效率高。儘管這個假設在現實中往往不成立，但單純貝氏分類器在許多應用（如文本分類）中仍然表現得相當不錯。

#9

★★★★

卜瓦松分佈（Poisson Distribution）通常用於模擬什麼類型的事件？

A

連續測量值（如身高、溫度）

B

在一個固定的時間間隔或空間區域內，獨立且隨機發生的事件的次數（例如，一小時內到達客服中心的電話數量）

C

一系列試驗中成功的比例

D

從有限母體中不放回抽樣得到的特定項目數量

答案解析

卜瓦松分佈是一種離散機率分佈，描述的是在固定單位時間、空間或體積內，某種稀有事件（事件之間相互獨立，且發生率 λ 在該單位內是常數）發生的次數 k 的機率。其應用場景包括：

單位時間內到達某服務點的顧客數。
單位長度內某材料的瑕疵數。
單位面積內某種植物的數量。
單位時間內網站收到的點擊數。

選項 B 正確描述了卜瓦松過程的特徵。選項 A 是連續變數。選項 C 可能涉及二項分佈。選項 D 描述的是超幾何分佈（Hypergeometric Distribution）。

#10

★★★★

指數分佈（Exponential Distribution）通常用於模擬什麼？

A

固定次數試驗中成功的次數

B

獨立且隨機發生的事件之間的時間間隔，或者直到下一個事件發生的等待時間（假設事件發生率恆定）

C

對稱分佈的連續測量值

D

多個類別的比例

答案解析

指數分佈是一種連續機率分佈，它與卜瓦松過程密切相關。如果事件的發生遵循卜瓦松過程（即事件在單位時間內發生的平均次數 λ 是常數），那麼兩次連續事件之間的時間間隔，或者從任意時間點開始直到下一個事件發生的等待時間，就服從指數分佈。其應用場景包括：

顧客到達服務點的時間間隔。
電子元件的壽命（假設故障率恆定）。
放射性粒子衰變的時間間隔。

指數分佈具有「無記憶性」（Memoryless Property），即過去等待了多久不影響未來還需要等待多久。選項 A 是二項分佈。選項 C 常為常態分佈。選項 D 可能用多項分佈。

#11

★★★★

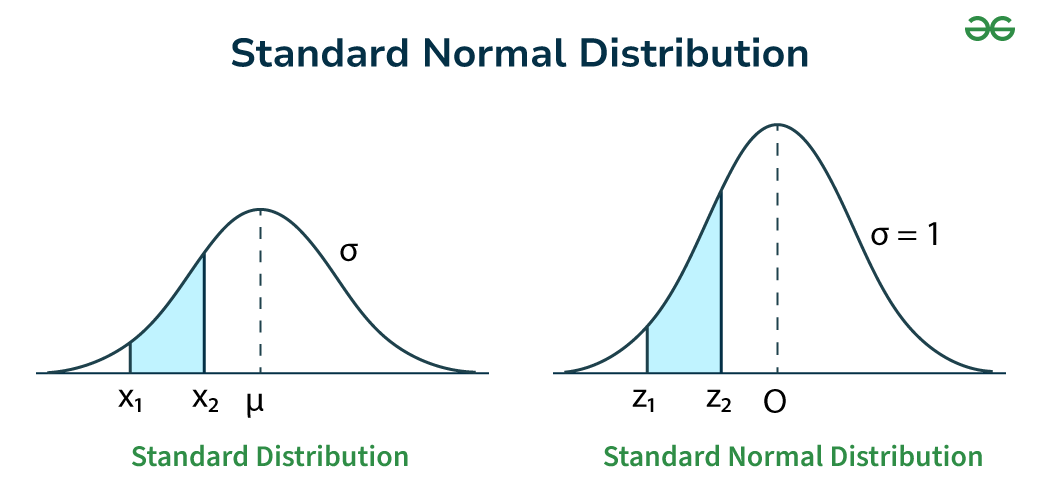
標準常態分佈（Standard Normal Distribution）是指平均數 μ 和標準差 σ 分別為多少的常態分佈？

A

μ=1, σ=1

B

μ=0, σ=1

C

μ=0, σ=0

D

μ 由數據決定, σ=1

答案解析

標準常態分佈是常態分佈家族中的一個特例，其平均數 μ 固定為 0，標準差 σ 固定為 1。任何一個服從平均數為 μ、標準差為 σ 的常態分佈的隨機變數 X，都可以通過 Z = (X - μ) / σ 的轉換（即計算 Z 分數），將其標準化為服從標準常態分佈的隨機變數 Z。標準常態分佈的機率值有標準化的表格（Z 表）或函數可供查詢，因此在統計計算中非常重要。

#12

★★★★

根據中央極限定理，當樣本大小 n 增大時，樣本平均數的分佈會發生什麼變化？

A

分佈的平均數會偏離母體平均數

B

分佈會越來越接近常態分佈，且分佈的標準差（標準誤）會減小

C

分佈會越來越偏離常態分佈

D

分佈的標準差會增大

答案解析

中央極限定理（CLT）說明了樣本平均數抽樣分佈的兩個重要特性隨樣本大小 n 的變化：

趨近常態：無論母體分佈如何，只要 n 足夠大，樣本平均數的分佈就會近似於常態分佈。
標準誤減小：樣本平均數分佈的標準差，即標準誤 (SE)，等於 σ/√n。當樣本大小 n 增大時，標準誤 σ/√n 會減小。這意味著隨著樣本量的增加，樣本平均數會更緊密地圍繞在母體平均數 μ 周圍，即樣本平均數作為母體平均數估計量的精度會提高。

因此，選項 B 正確描述了這兩個變化。

#13

★★★

機率密度函數（Probability Density Function, PDF）f(x) 對於連續隨機變數 X 的主要作用是？

A

直接給出 X 取某個特定值 x 的機率 P(X=x)

B

描述 X 在不同數值點附近的相對可能性，其在某個區間 [a, b] 上的積分等於 X 落在該區間的機率 P(a ≤ X ≤ b)

C

計算 X 的期望值 E[X]

D

計算 X 的變異數 Var(X)

答案解析

對於連續隨機變數，其取任何一個特定單點值的機率理論上為 0（A 錯誤）。我們關心的是變數落在某個區間內的機率。機率密度函數 PDF f(x) 本身並非機率值，但它描述了變數在數值 x 附近單位寬度內的機率密度（相對可能性）。要計算變數 X 落在區間 [a, b] 內的機率 P(a ≤ X ≤ b)，需要計算 PDF 曲線在該區間下方的面積，即對 f(x) 從 a 到 b 進行積分（∫[a,b] f(x) dx）（B 正確）。雖然 PDF 可以用來計算期望值（∫ x*f(x) dx）和變異數（∫ (x-μ)^2*f(x) dx），但其主要作用是定義和計算區間機率。

#14

★★★★

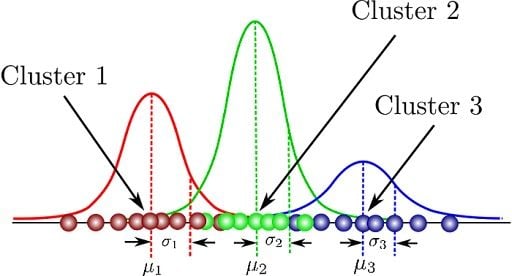
在機器學習中，高斯混合模型（Gaussian Mixture Model, GMM）是一種基於機率模型的什麼演算法？

A

監督式分類演算法

B

無監督式聚類演算法

C

強化學習演算法

D

降維演算法

答案解析

高斯混合模型（GMM）假設數據是由 K 個不同的常態（高斯）分佈所混合生成的。它是一種基於機率的聚類演算法，屬於無監督學習。GMM 的目標是找出這 K 個高斯分佈的參數（每個分佈的平均數、共變異數矩陣以及它們在混合中的權重），使得模型能夠最好地擬合觀測到的數據。每個數據點可以被指派到它最可能隸屬的那個高斯分佈（群集），並且 GMM 可以提供每個數據點屬於每個群集的機率（軟聚類 Soft Clustering）。相較於 K-means（假設群集是球狀的），GMM 可以擬合更複雜的橢球狀群集。

#15

★★★

如果事件 A 和事件 B 是相互獨立（Independent）的，那麼 P(A and B) 等於多少？

A

P(A) + P(B)

B

P(A) * P(B)

C

P(A) / P(B)

D

0

答案解析

兩個事件 A 和 B 相互獨立的定義是，一個事件的發生不影響另一個事件發生的機率，即 P(A|B) = P(A) 且 P(B|A) = P(B)。根據條件機率的乘法法則 P(A and B) = P(A|B) * P(B) 或 P(A and B) = P(B|A) * P(A)，當 A 和 B 獨立時，可以直接推導出 P(A and B) = P(A) * P(B)。這是獨立事件聯合機率的計算公式。選項 A 是互斥事件聯集機率的公式（且需 P(A and B)=0）。

#16

★★★

隨機變數 X 的變異數（Variance）Var(X) 的計算公式是？

A

E[X]

B

E[X^2]

C

E[(X - E[X])^2] 或 E[X^2] - (E[X])^2

D

(E[X])^2

答案解析

變異數衡量隨機變數取值相對於其期望值（平均數）的離散程度。其定義是離差平方的期望值，即 Var(X) = E[(X - μ)^2]，其中 μ = E[X]。這個公式直觀地表示了變數偏離其平均數的平均平方距離。另一個常用的計算公式是 Var(X) = E[X^2] - (E[X])^2，即平方的期望值減去期望值的平方。這兩個公式是等價的。標準差則是變異數的平方根。

#17

★★★

伯努利試驗（Bernoulli Trial）指的是什麼？

A

進行無限多次的隨機試驗

B

只有兩種可能結果（如成功/失敗、是/否、正面/反面）的單次隨機試驗

C

結果可以是任何連續數值的試驗

D

至少有三種可能結果的試驗

答案解析

伯努利試驗是最簡單的隨機試驗模型，它描述的是只進行一次、且只有兩種互斥結果的試驗。通常將這兩種結果標記為「成功」（機率為 p）和「失敗」（機率為 1-p）。例如，投擲一次硬幣（正面/反面）、檢查一個產品是否合格（合格/不合格）、進行一次射門（進球/未進球）都可以視為伯努利試驗。多次獨立重複的伯努利試驗是構成二項分佈、幾何分佈等離散分佈的基礎。

#18

★★★

均勻分佈（Uniform Distribution）的主要特徵是？

A

機率密度集中在平均數附近

B

在一個指定的區間 [a, b] 內，所有數值的機率密度（對於連續型）或機率（對於離散型）都是相等的

C

分佈呈現明顯的向右偏斜

D

只可能取 0 或 1 兩個值

答案解析

均勻分佈描述的是「等可能性」。對於連續均勻分佈，在一個有限區間 [a, b] 內，任何長度相同的子區間具有相同的機率，其機率密度函數在區間 [a, b] 內是一個常數（1/(b-a)），在區間外為 0，圖形呈矩形。對於離散均勻分佈，如果一個變數有 n 個可能的結果，則每個結果發生的機率都是 1/n。選項 B 正確描述了這種等可能性的特徵。常態分佈集中在平均數附近（A）。指數分佈是右偏的（C）。伯努利分佈只取兩個值（D）。

#19

★★★★

將一個常態分佈的隨機變數 X 轉換為標準常態分佈的隨機變數 Z，使用的公式是？

A

Z = (X + μ) / σ

B

Z = (X - μ) * σ

C

Z = (X - μ) / σ

D

Z = X / μ

答案解析

標準化（Standardization）是將服從任意常態分佈 N(μ, σ^2) 的隨機變數 X 轉換為服從標準常態分佈 N(0, 1) 的隨機變數 Z 的過程。這個轉換公式就是計算 X 的 Z 分數：先將 X 減去其平均數 μ（使新的平均數為 0），然後再除以其標準差 σ（使新的標準差為 1）。即 Z = (X - μ) / σ。這個轉換使得不同常態分佈的數值可以在同一個標準尺度上進行比較和查表計算機率。

#20

★★★

在探索資料分佈時，密度圖（Density Plot 或 Kernel Density Estimate, KDE）相比於直方圖的主要優勢是？

A

可以顯示每個數據點的精確值

B

提供一個更平滑的連續曲線來估計數據的機率密度函數，不受組距（bin）寬度選擇的影響

C

只能用於離散數據

D

計算速度遠快於直方圖

答案解析

直方圖的形狀會受到組距（bin）數量和寬度選擇的影響，不同的選擇可能呈現出不同的分佈樣貌。密度圖（特別是核密度估計 KDE）透過在每個數據點放置一個平滑的核函數（如高斯核），然後將這些核函數疊加起來，得到一個連續、平滑的曲線來估計數據的潛在機率密度函數。它不受 bin 選擇的影響，能更好地呈現分佈的形狀（如峰值、偏態），尤其是在樣本量較大時。然而，KDE 也有其參數（如核函數的帶寬 bandwidth）需要選擇。選項 A 錯誤。選項 C 錯誤，主要用於連續數據。選項 D 不一定，KDE 計算可能更複雜。

#21

★★★

貝氏定理（Bayes' Theorem）提供了一種更新機率的方法，它描述了哪個機率與哪個機率之間的關係？

A

邊際機率（Marginal Probability）和聯合機率（Joint Probability）

B

後驗機率（Posterior Probability）與事前機率（Prior Probability）、概度（Likelihood）和證據（Evidence）

C

條件機率（Conditional Probability）和互斥事件的機率

D

獨立事件的機率和相依事件的機率

答案解析

貝氏定理的公式通常寫為：P(A|B) = [P(B|A) * P(A)] / P(B)。它描述了在觀察到證據 B 之後，事件 A 發生的後驗機率 P(A|B) 如何從事件 A 的事前機率 P(A)（在觀察到 B 之前的信念）透過概度 P(B|A)（假設 A 發生時，觀察到 B 的機率）和證據 B 的邊際機率 P(B)（觀察到 B 的總機率）來更新。即：後驗機率 ∝ 概度 × 事前機率。貝氏定理是貝氏統計推斷和許多機器學習演算法（如貝氏分類器）的基礎。

#22

★★

隨機變數 X 的累積分布函數（Cumulative Distribution Function, CDF）F(x) 定義為？

A

P(X = x)

B

P(X ≤ x)

C

P(X > x)

D

f(x)，即機率密度函數

答案解析

累積分布函數（CDF）F(x) 給出的是隨機變數 X 的取值小於或等於某個特定值 x 的機率，即 F(x) = P(X ≤ x)。無論是離散還是連續隨機變數，CDF 都是一個非遞減函數，其值域為 [0, 1]。對於連續變數，CDF 是其 PDF 的積分；對於離散變數，CDF 是其機率質量函數（Probability Mass Function, PMF）的累加和。CDF 完整地描述了一個隨機變數的機率分佈。

#23

★★

幾何分佈（Geometric Distribution）描述的是在重複獨立的伯努利試驗中，什麼事件發生的機率？

A

恰好觀察到 k 次成功

B

直到第一次成功出現時，所需要進行的試驗次數

C

在固定時間內成功的次數

D

試驗成功的比例

答案解析

幾何分佈也是基於一系列獨立的伯努利試驗（每次成功機率為 p）。它關注的是第一次成功發生前的失敗次數，或者直到第一次成功發生所需的總試驗次數（這兩種定義略有不同，但都屬於幾何分佈）。例如，不斷投擲一枚硬幣直到第一次出現正面，投擲的次數就服從幾何分佈。選項 A 是二項分佈。選項 C 是卜瓦松分佈。選項 D 是一個比例。

#24

★★★

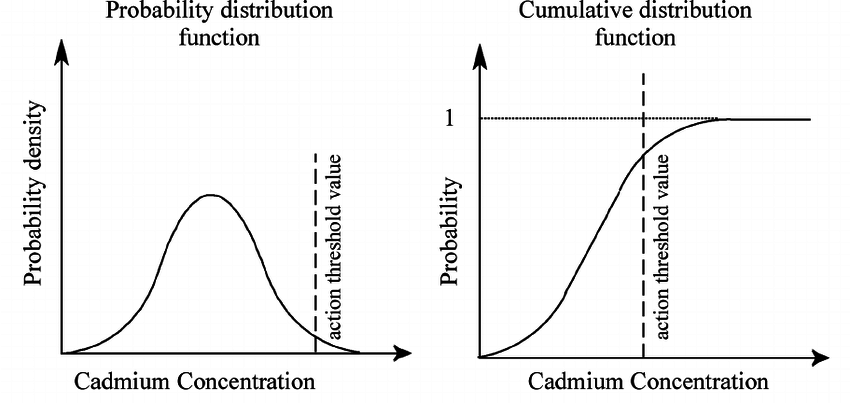
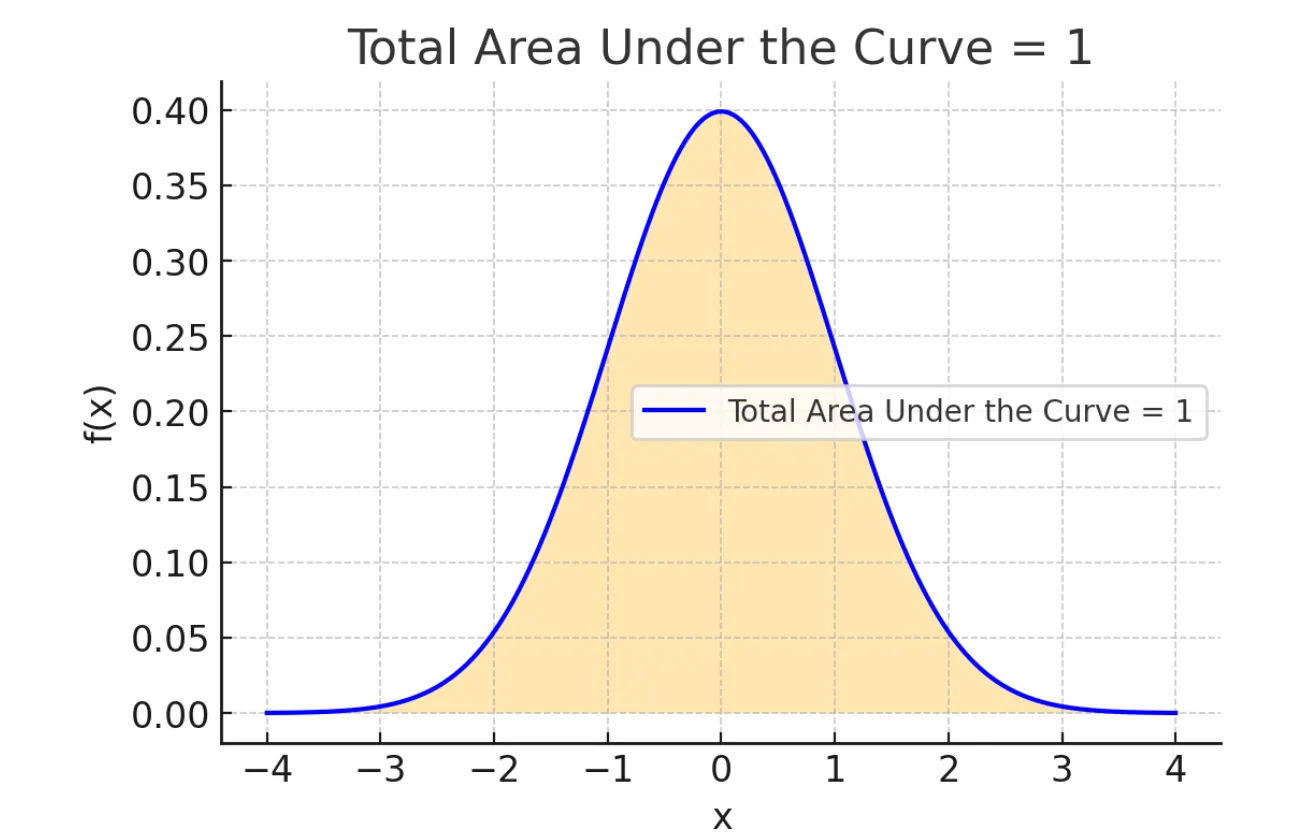
常態分佈的機率密度曲線下方的總面積等於多少？

A

0

B

1

C

平均數 μ

D

標準差 σ

答案解析

對於任何有效的機率密度函數（PDF），其定義域內（通常是負無窮到正無窮）曲線下方的總面積必須等於 1。這代表了隨機變數取所有可能值的總機率為 1（即必然事件的機率）。常態分佈作為一種連續機率分佈，其 PDF 曲線下方的總面積也必須等於 1。

#25

★★★

中央極限定理（CLT）成立的一個重要前提條件（或要求）是？

A

母體分佈必須是常態分佈

B

抽取的樣本必須是獨立且來自相同分佈（Independent and Identically Distributed, i.i.d.），且樣本數 n 足夠大

C

樣本大小 n 必須小於 30

D

母體標準差必須已知

答案解析

中央極限定理的應用有幾個關鍵條件：

獨立同分佈 (i.i.d.)：從母體中抽取的樣本觀測值之間必須相互獨立，並且都來自同一個母體分佈。（這是許多統計推斷的基礎假設）
樣本數足夠大 (n is large enough)：通常認為 n ≥ 30 是一個經驗法則，但對於接近常態的母體，較小的 n 可能就足夠；對於偏度很大的母體，則需要更大的 n。
母體變異數有限 (Finite Variance)：母體分佈需要有有限的變異數 σ^2。

CLT 最強大的地方在於它對母體分佈的形狀沒有嚴格要求（A 錯誤），只要滿足 i.i.d.、n 足夠大和變異數有限，樣本平均數的分佈就會趨近常態。選項 C 錯誤。母體標準差是否已知（D）會影響後續推斷方法的選擇（Z 檢定 vs. t 檢定），但不是 CLT 成立的前提。

#26

★★★

卡方適合度檢定（Chi-squared Goodness-of-Fit Test）通常用於檢定什麼？

A

兩個數值變數的平均數是否相等

B

觀測到的樣本頻率分佈是否符合某個預期的理論分佈（例如，骰子各點數出現的頻率是否符合均勻分佈）

C

兩個數值變數之間是否存在線性相關

D

樣本數據是否服從常態分佈

答案解析

卡方適合度檢定是一種非參數檢定方法，用於比較一組類別數據的觀測頻數（Observed Frequencies）與基於某個理論假設或預期機率分佈計算出的期望頻數（Expected Frequencies）之間是否存在顯著差異。虛無假設（Null Hypothesis）通常是觀測分佈與理論分佈沒有差異。如果計算出的卡方統計量大於臨界值（或 p 值小於顯著水準），則拒絕虛無假設，認為觀測分佈與理論分佈存在顯著差異。它常用於檢定骰子是否公平、孟德爾遺傳定律的比例是否符合預期等。選項 A 可用 t 檢定或 ANOVA。選項 C 可用相關係數檢定。選項 D 有專門的常態性檢定方法（如 Shapiro-Wilk test, K-S test）或透過 Q-Q 圖判斷。

#27

★★★

在推薦系統中，可以使用機率模型來估計一個使用者對一個物品評分的機率分佈，這屬於哪種機器學習任務？

A

聚類（Clustering）

B

機率預測（Probabilistic Prediction）或回歸（Regression，如果評分視為連續）

C

降維（Dimensionality Reduction）

D

異常檢測（Anomaly Detection）

答案解析

推薦系統的目標是預測使用者對他們尚未接觸過的物品的偏好或評分。當使用機率模型（例如基於矩陣分解的機率模型或貝氏個人化排序 BPR）來估計使用者給予物品特定評分（或評分區間）的機率時，這本質上是在進行一個機率預測任務。如果將評分視為一個連續的數值（即使可能是有限範圍的，如 1-5 星），也可以看作是一個回歸問題，只是模型輸出的是一個預測分佈而非單一點估計。這與無監督的聚類、降維或異常檢測任務不同。

#28

★★

事件 A 的補集（Complement）A' 的機率 P(A') 與 P(A) 的關係是？

A

P(A') = P(A)

B

P(A') = 1 / P(A)

C

P(A') = 1 - P(A)

D

P(A') = 0

答案解析

事件 A 的補集 A'（或寫作 A^c）是指在樣本空間 S 中，所有不屬於事件 A 的結果所構成的事件。事件 A 和其補集 A' 是互斥的（它們不可能同時發生），並且它們的聯集構成了整個樣本空間（A ∪ A' = S）。根據機率公理 P(S) = 1 和互斥事件的可加性 P(A ∪ A') = P(A) + P(A')，我們可以得到 P(A) + P(A') = 1。因此，補集的機率 P(A') = 1 - P(A)。

#29

★★★

如果隨機變數 X 的所有可能取值都乘以一個常數 c，其期望值 E[cX] 會如何變化？

A

變為 E[X] / c

B

變為 c * E[X]

C

變為 E[X] + c

D

保持不變

答案解析

期望值具有線性性質。根據期望值的定義 E[cX] = Σ [(c * xi) * P(X=xi)]。由於常數 c 可以提出求和符號外，得到 E[cX] = c * Σ [xi * P(X=xi)] = c * E[X]。也就是說，一個常數乘以一個隨機變數的期望值，等於該常數乘以該隨機變數的期望值。

#30

★★★

二項分佈 B(n, p) 的平均數（期望值）和變異數分別是多少？

A

平均數=np, 變異數=np

B

平均數=np, 變異數=np(1-p)

C

平均數=n/p, 變異數=n(1-p)/p^2

D

平均數=p, 變異數=p(1-p)

答案解析

對於一個服從二項分佈 B(n, p) 的隨機變數（代表 n 次獨立伯努利試驗中成功的次數，每次成功機率為 p），其期望值（平均成功次數）為 E[X] = np，其變異數為 Var(X) = np(1-p)。選項 D 是單次伯努利試驗的期望值和變異數。

#31

★★★

指數分佈的機率密度函數（PDF）具有什麼特性？

A

對稱的鐘形

B

單調遞減且恆為正（對於 x > 0）

C

U 形

D

在某個區間內為常數

答案解析

指數分佈的機率密度函數為 f(x) = λ * exp(-λx)，其中 x ≥ 0 且 λ > 0（λ 是事件發生率）。這個函數在 x=0 時取得最大值 λ，然後隨著 x 的增加而指數級地單調遞減，趨近於 0。因此，它是一個典型的右偏分佈，表示短時間間隔發生的機率較高，長時間間隔發生的機率較低。選項 A 是常態分佈。選項 D 是均勻分佈。

#32

★★★

常態分佈在哪個值達到其峰值（即眾數）？

A

平均數（μ）

B

平均數 + 一個標準差（μ + σ）

C

平均數 - 一個標準差（μ - σ）

D

0

答案解析

常態分佈的機率密度函數曲線是對稱的鐘形，其對稱軸位於平均數 μ 處。曲線的最高點（峰值），也就是隨機變數最可能取值（或取值密度最大）的地方，正好就是平均數 μ。同時，由於對稱性，常態分佈的平均數、中位數和眾數是相等的，都等於 μ。

#33

★★★

抽樣分佈（Sampling Distribution）指的是什麼的分佈？

A

原始母體數據的分佈

B

從同一母體中抽取的所有可能樣本（或大量樣本）的某個統計量（如樣本平均數、樣本比例）的分佈

C

單個樣本內數據點的分佈

D

理論機率分佈（如常態分佈）

答案解析

抽樣分佈不是指單個樣本的分佈，也不是指母體的分佈。它是指樣本統計量（例如樣本平均數、樣本變異數、樣本比例等）的機率分佈。想像一下，我們從同一個母體中反覆抽取大小為 n 的樣本，每次都計算一個統計量（如樣本平均數）。將所有這些計算出的樣本統計量收集起來，它們自身會形成一個分佈，這個分佈就叫做該統計量的抽樣分佈。理解抽樣分佈對於進行統計推斷（估計母體參數、進行假設檢定）至關重要，例如中央極限定理描述的就是樣本平均數的抽樣分佈。

#34

★★★

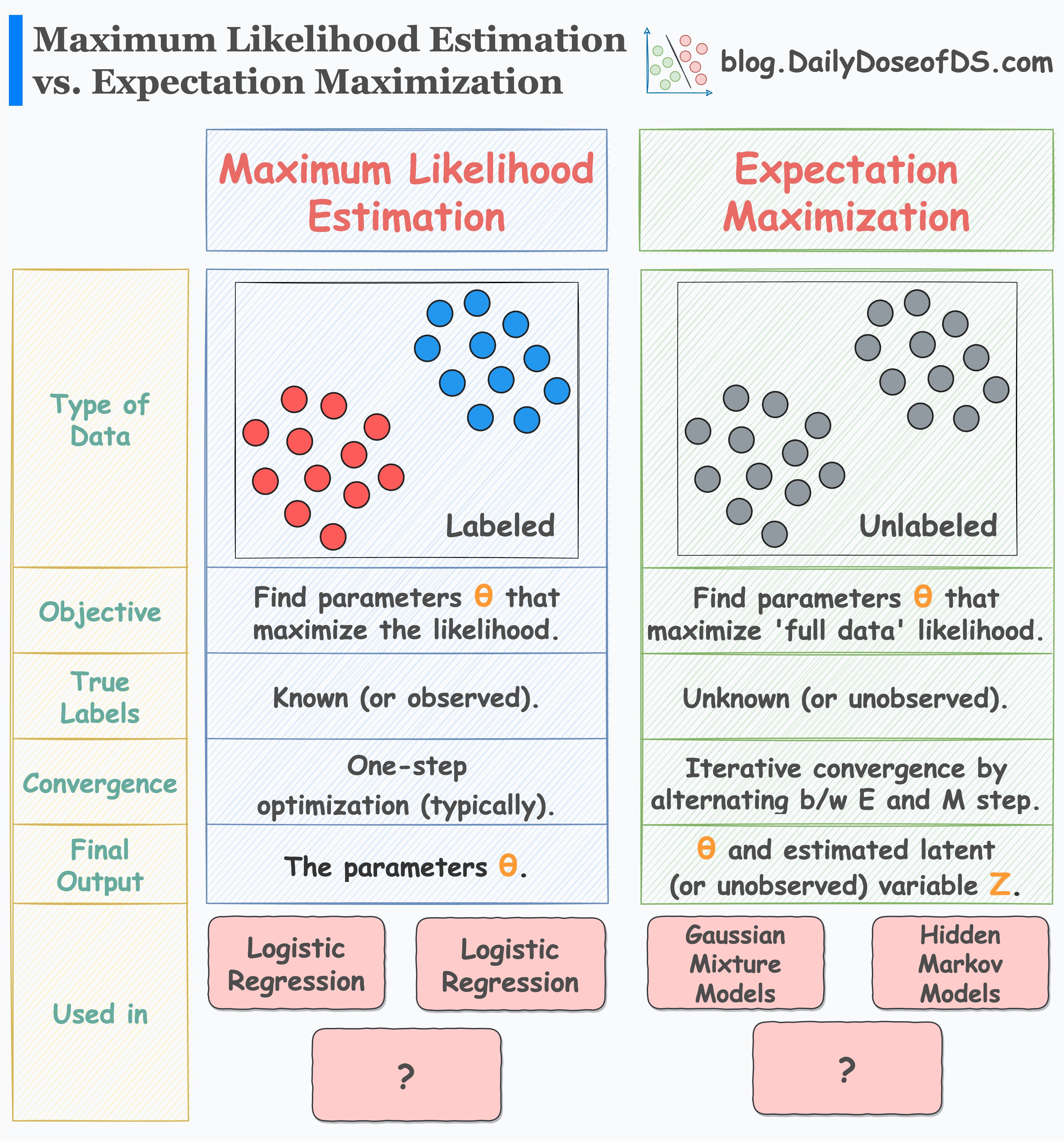
最大概度估計（Maximum Likelihood Estimation, MLE）是一種常用的參數估計方法，其基本思想是？

A

選擇使得事前機率最大的參數值

B

選擇一組參數值，使得在這些參數下觀測到當前樣本數據的聯合機率（概度）最大化

C

選擇使得模型誤差平方和最小的參數值

D

選擇使得後驗機率最大的參數值

答案解析

最大概度估計（MLE）是頻率學派統計中一種常用的點估計方法。假設我們有一個機率模型（其形式已知，但包含未知參數 θ），並且觀察到了一組樣本數據 D。MLE 的目標是找到一組參數值 θ^，使得在參數為 θ^ 的條件下，觀察到數據 D 的機率（稱為概度函數 L(θ|D) = P(D|θ)）達到最大。直觀地說，就是找到最可能產生我們所觀察到的數據的那組參數值。選項 C 描述的是最小平方法（Least Squares Estimation），常用於回歸。選項 D 描述的是最大後驗機率估計（Maximum A Posteriori, MAP），屬於貝氏推斷。

#35

★★★

在隱馬可夫模型（Hidden Markov Model, HMM）中，「隱藏」（Hidden）指的是什麼？

A

模型的轉移機率是隱藏的

B

模型內部的狀態（States）序列是無法直接觀測到的，只能透過可觀測的輸出序列來推斷

C

模型的輸出機率是隱藏的

D

模型的初始狀態分佈是隱藏的

答案解析

隱馬可夫模型（HMM）是一種用於描述含有隱藏狀態的馬可夫過程的統計模型。它包含兩個序列：一個是無法直接觀察到的隱藏狀態序列（遵循馬可夫鏈，即當前狀態只依賴於前一個狀態），另一個是可以觀察到的輸出符號序列。模型的假設是，每個輸出符號的生成機率僅僅依賴於當前的隱藏狀態。由於我們只能觀察到輸出序列，而無法直接知道系統處於哪個隱藏狀態，因此這些狀態被稱為「隱藏」的。HMM 的典型任務包括：給定模型和觀測序列，計算該序列出現的機率；給定模型和觀測序列，找出最可能的隱藏狀態序列（解碼問題）；給定觀測序列，學習模型的參數（轉移機率、輸出機率、初始狀態分佈）。HMM 廣泛應用於語音識別、自然語言處理（如詞性標註）、生物資訊學等領域。

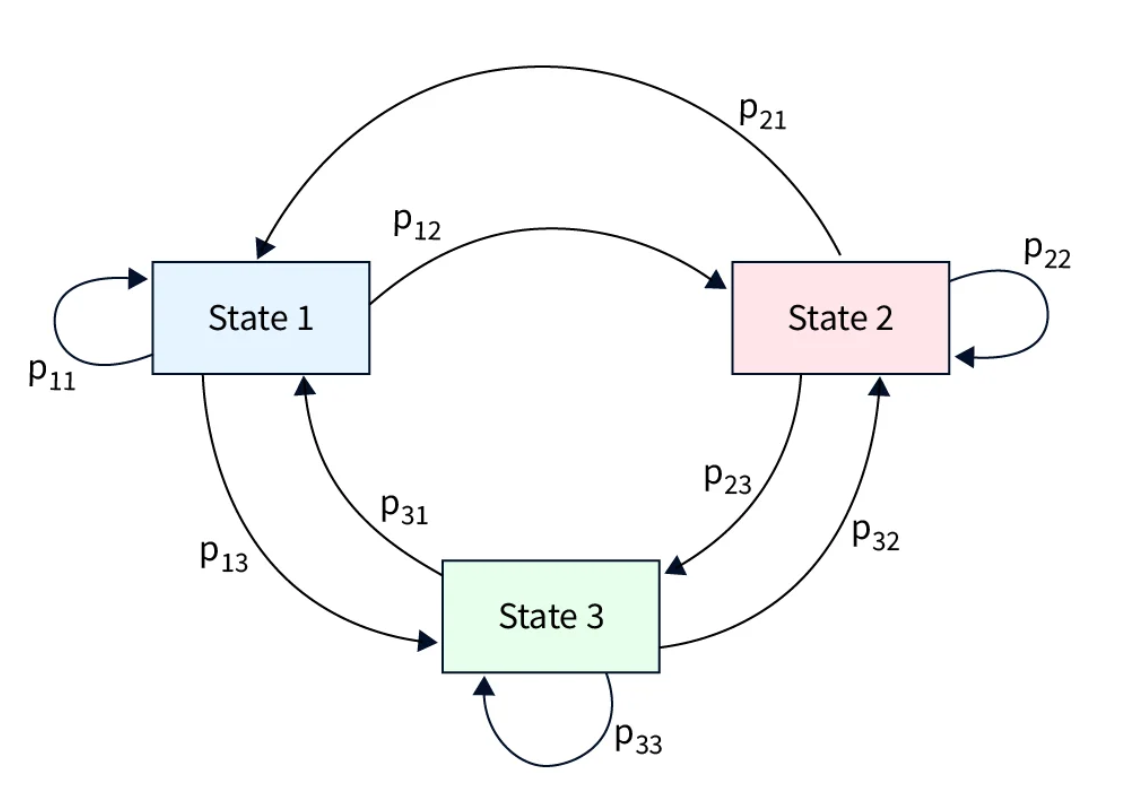
#36

★★★

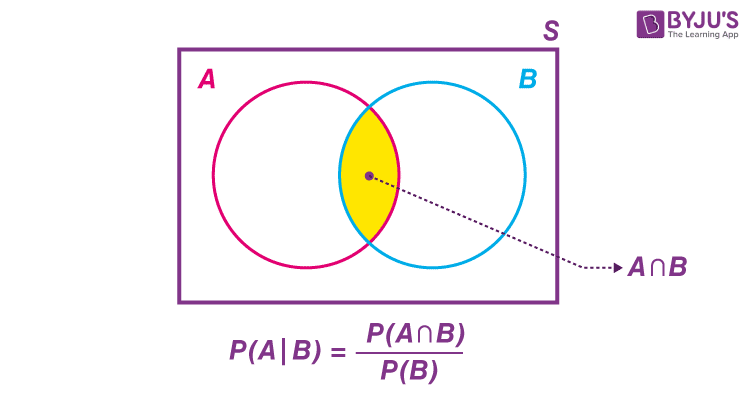
條件機率 P(A|B) 指的是什麼？

A

事件 A 和事件 B 同時發生的機率

B

在事件 B 已經發生的條件下，事件 A 發生的機率

C

事件 A 或事件 B 發生的機率

D

事件 A 不發生的機率

答案解析

條件機率 P(A|B) 衡量的是當我們知道事件 B 已經發生（或者說，將樣本空間限制在 B 發生的結果中）時，事件 A 也會發生的機率。其計算公式為 P(A|B) = P(A and B) / P(B)，前提是 P(B) > 0。條件機率是理解事件間依賴關係和進行統計推斷的基礎概念。選項 A 是聯合機率 P(A and B)。選項 C 是聯集機率 P(A or B)。選項 D 是補集機率 P(A')。

#37

★★★

如果隨機變數 X 和 Y 相互獨立，則它們的共變異數（Covariance）Cov(X, Y) 等於多少？

A

0

B

1

C

-1

D

Var(X) * Var(Y)

答案解析

共變異數 Cov(X, Y) = E[(X - E[X])(Y - E[Y])] 衡量兩個隨機變數之間線性關係的強度和方向。如果 X 和 Y 相互獨立，那麼 E[XY] = E[X]E[Y]。根據共變異數的另一個計算公式 Cov(X, Y) = E[XY] - E[X]E[Y]，當 X 和 Y 獨立時，Cov(X, Y) = E[X]E[Y] - E[X]E[Y] = 0。因此，獨立的隨機變數其共變異數必定為 0。需要注意的是，反之不一定成立：共變異數為 0 僅表示兩者沒有線性關係，但可能存在非線性關係，因此不一定相互獨立（除非它們服從多元常態分佈）。

#38

★★

下列哪個機率分佈通常用於模擬壽命、等待時間等非負連續變數？

A

常態分佈（Normal Distribution）

B

二項分佈（Binomial Distribution）

C

指數分佈（Exponential Distribution）或韋伯分佈（Weibull Distribution）

D

卜瓦松分佈（Poisson Distribution）

答案解析

壽命、等待時間等變數具有非負（必然大於等於零）且連續的特性。指數分佈是模擬這類變數的常用模型，特別是當事件發生率（或故障率）被假設為常數時。韋伯分佈是更廣義的模型，可以模擬故障率隨時間增加、減少或恆定的情況，也常用於可靠性工程和生存分析。常態分佈的取值範圍是負無窮到正無窮，不適合直接模擬非負變數（儘管在某些情況下可用作近似）。二項分佈和卜瓦松分佈是離散分佈。

#39

★★★

標準常態分佈的累積分布函數（CDF）通常用哪個符號表示？

A

Φ(z)

B

φ(z)

C

Γ(z)

D

B(n, p)

答案解析

標準常態分佈的累積分布函數（CDF），即 P(Z ≤ z)，在統計學中通常用大寫的希臘字母 Phi（Φ）來表示，寫作 Φ(z)。它表示標準常態變數 Z 的取值小於或等於某個值 z 的機率。而標準常態分佈的機率密度函數（PDF）通常用小寫的希臘字母 phi（φ）表示，φ(z) = (1/√(2π)) * exp(-z^2/2)。Γ(z) 是 Gamma 函數。B(n, p) 是二項分佈的表示法。

#40

★★

大數法則（Law of Large Numbers, LLN）主要說明了什麼現象？

A

樣本平均數的分佈趨近常態分佈

B

當獨立重複試驗的次數趨近無窮大時，樣本平均數會收斂到母體期望值（平均數）

C

樣本變異數總是等於母體變異數

D

機率值必定介於 0 和 1 之間

答案解析

大數法則是機率論中的另一個基本定理。它描述了樣本平均數的穩定性。簡單來說，當我們對一個隨機現象進行越來越多次的獨立重複觀測時，觀測結果的算術平均值（樣本平均數）會越來越接近該現象的真實期望值（母體平均數）。例如，重複投擲一枚公正硬幣，出現正面的比例會隨著投擲次數的增加而越來越接近 0.5。大數法則為使用樣本平均數來估計母體平均數提供了理論基礎。選項 A 描述的是中央極限定理。

#41

★★

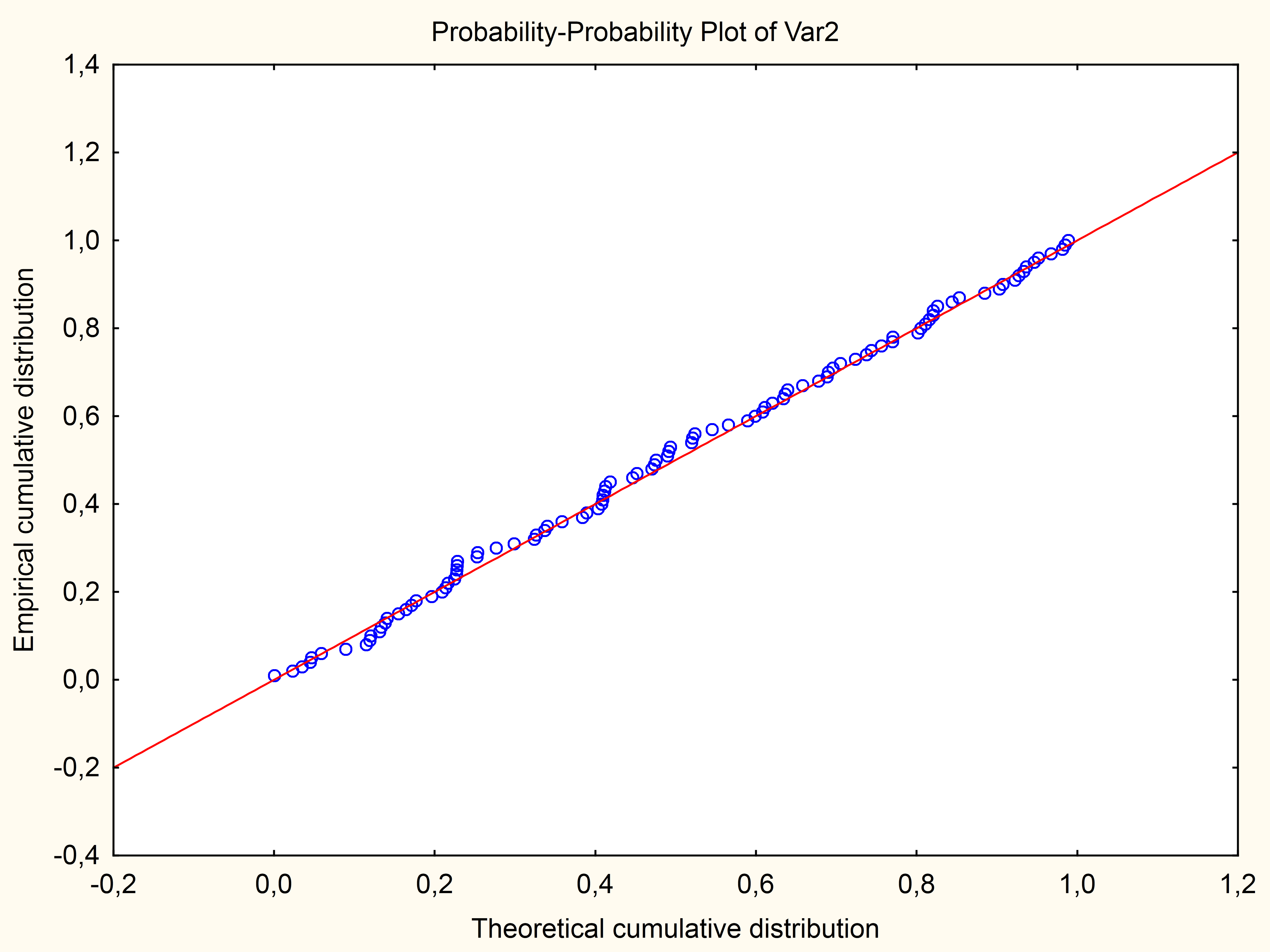
P-P 圖（Probability-Probability Plot）與 Q-Q 圖類似，也用於比較分佈，但它的座標軸繪製的是什麼？

A

機率密度函數值

B

累積機率（Cumulative Probabilities）

C

期望值

D

變異數

答案解析

P-P 圖也是一種比較兩個機率分佈（通常是一個樣本分佈和一個理論分佈）的圖形方法。與 Q-Q 圖繪製分位數不同，P-P 圖繪製的是兩個分佈對應的累積機率。對於一系列的數值點，計算其在樣本分佈中的經驗累積機率（Empirical CDF value）和在理論分佈中的理論累積機率（Theoretical CDF value），然後將這兩組累積機率值作為 (X, Y) 座標繪製散佈圖。如果兩個分佈吻合，點應該落在 y=x 的對角線上。P-P 圖對分佈中心部分的差異比 Q-Q 圖更敏感，而 Q-Q 圖對分佈尾部的差異更敏感。

#42

★★★

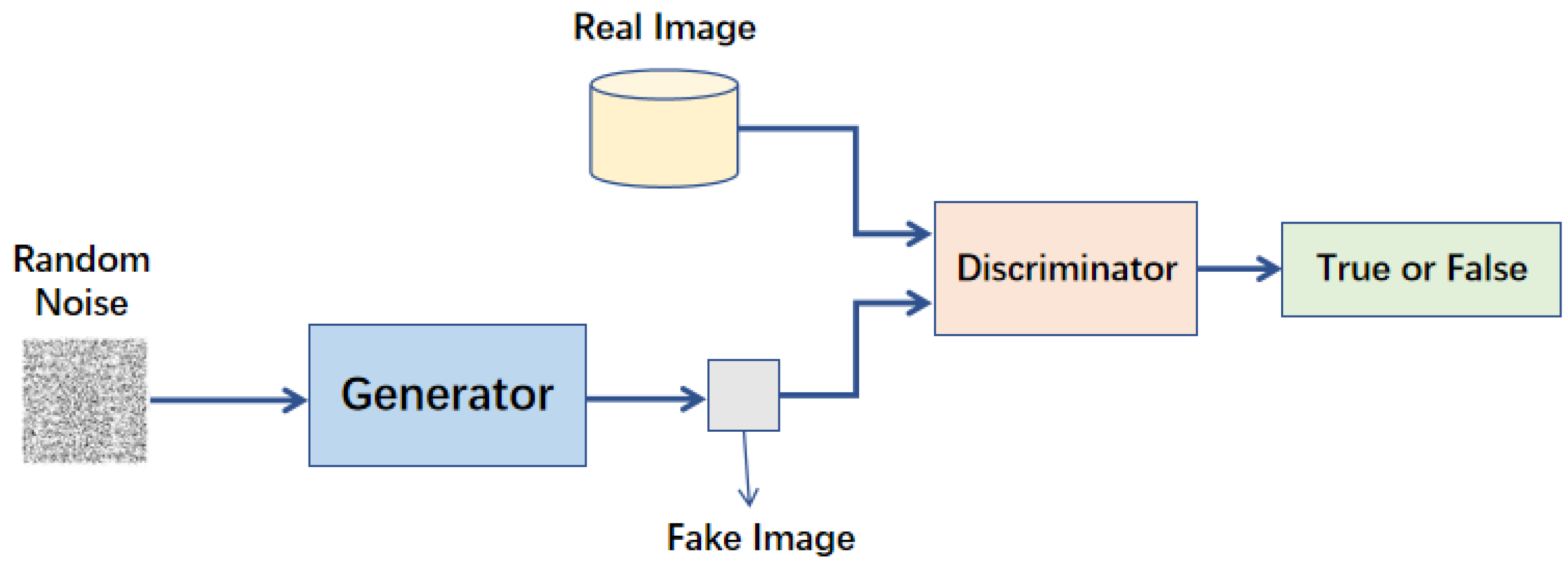
在生成對抗網路（Generative Adversarial Network, GAN）中，生成器（Generator）試圖學習什麼？

A

判斷輸入數據是真實的還是生成的

B

學習真實數據的潛在機率分佈，並生成與真實數據相似的新樣本

C

將高維數據映射到低維空間

D

最大化分類任務的準確率

答案解析

GAN 包含兩個相互競爭的神經網路：生成器（G）和判別器（D）。生成器的目標是學習訓練數據（如真實圖像）的潛在機率分佈。它接收隨機噪聲作為輸入，並嘗試生成看起來像真實數據的假樣本。判別器（A）則學習如何區分真實樣本和生成器生成的假樣本。兩者透過對抗訓練過程相互改進：生成器努力生成更逼真的樣本來欺騙判別器，判別器則努力提高辨別真偽的能力。最終目標是讓生成器能夠生成與真實數據分佈非常相似、難以被判別器區分的新樣本。

#43

★★★

如果一系列事件的發生遵循卜瓦松過程，且平均每小時發生 3 次，那麼在接下來的 2 小時內恰好發生 5 次事件的機率，應該使用哪個分佈來計算？

A

二項分佈 B(5, 3/5)

B

卜瓦松分佈，其參數 λ = 3 * 2 = 6

C

指數分佈，其參數 λ = 6

D

常態分佈 N(6, 6)

答案解析

卜瓦松分佈描述在固定區間內事件發生的次數。如果事件發生率是恆定的，那麼在一個長度為 t 的區間內，事件發生的平均次數（即卜瓦松分佈的參數 λ'）等於單位區間內的平均發生率 λ 乘以區間長度 t。本題中，單位時間（1 小時）內的平均發生率 λ = 3。我們關心的是在 2 小時這個區間內發生的次數，因此這個新區間對應的卜瓦松參數 λ' = λ * t = 3 * 2 = 6。我們需要計算的是服從參數為 6 的卜瓦松分佈的隨機變數取值為 5 的機率 P(X=5 | λ'=6)。

#44

★★★

為何常態分佈在統計推斷中如此重要？主要原因之一是？

A

所有真實世界的數據都完美服從常態分佈

B

根據中央極限定理，許多樣本統計量（如樣本平均數）的分佈在大樣本下會趨近常態分佈

C

常態分佈的計算最為簡單

D

常態分佈可以用來模擬任何類型的數據

答案解析

常態分佈之所以重要，並非因為所有數據都服從它（A 錯誤），也不是因為它能模擬所有數據（D 錯誤）或計算最簡單（C 不一定）。其核心重要性很大程度上源於中央極限定理（CLT）。CLT 告訴我們，即使原始母體數據不是常態分佈，只要樣本量足夠大，樣本平均數的抽樣分佈也會近似常態分佈。這使得我們可以利用常態分佈的良好數學性質來對樣本平均數進行假設檢定和信賴區間估計，即使我們不知道母體的確切分佈。此外，許多自然和社會現象的測量誤差也傾向於服從常態分佈。

#45

★★

下列哪種圖表最不適合用於視覺化單一連續變數的分佈？

A

直方圖（Histogram）

B

箱型圖（Box Plot）

C

密度圖（Density Plot）

D

散佈圖（Scatter Plot）

答案解析

直方圖、箱型圖和密度圖都是常用於視覺化單一連續變數分佈的工具，它們各自從不同角度展示數據的集中趨勢、離散程度、分佈形狀和異常值。散佈圖則是用於展示兩個連續變數之間的關係，需要 X 軸和 Y 軸兩個變數，因此不適合用於視覺化單一變數的分佈。

#46

★★★

在自然語言處理中，語言模型（Language Model）通常是基於什麼來預測下一個詞彙？

A

整個文檔的主題

B

給定前面詞彙序列的條件下，下一個詞彙出現的機率分佈

C

詞彙的詞性標籤

D

句子的語法結構

答案解析

語言模型的核心任務是學習詞彙序列的機率分佈。給定一個詞彙序列（即前面出現的詞彙），語言模型會計算詞彙表中每個詞彙作為下一個詞彙出現的條件機率 P(下一個詞 | 前面詞彙序列)。基於這個機率分佈，模型可以預測最可能出現的下一個詞彙，或者從這個分佈中進行抽樣來生成文本。這是許多 NLP 應用（如機器翻譯、文本生成、語音識別）的基礎。

#47

★

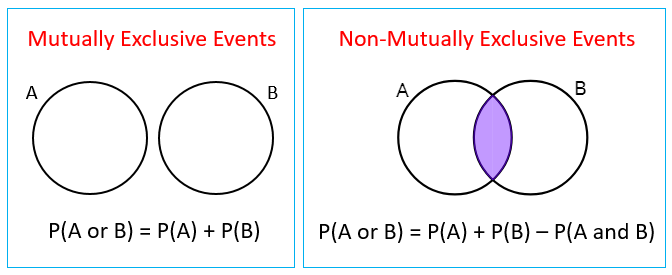
互斥（Mutually Exclusive）事件是指？

A

兩個或多個事件不能同時發生

B

一個事件的發生不影響另一個事件的發生機率

C

兩個事件必定同時發生

D

兩個事件的聯集是整個樣本空間

答案解析

如果兩個事件 A 和 B 是互斥的（或稱互不相容 Disjoint），則意味著它們不可能在同一次試驗中同時發生。換句話說，它們的交集是空集合（A ∩ B = ∅），因此它們同時發生的機率 P(A and B) = 0。例如，投擲一次骰子，得到點數 1 和得到點數 2 就是互斥事件。選項 B 描述的是獨立事件。

#48

★★

如果隨機變數 X 的變異數 Var(X) = 9，那麼它的標準差（Standard Deviation）是多少？

A

81

B

3

C

9

D

1.5

答案解析

標準差定義為變異數的正平方根。因此，如果變異數 Var(X) = 9，那麼標準差 σ = √Var(X) = √9 = 3。標準差的單位與原始隨機變數相同，而變異數的單位是原始變數單位的平方。

#49

★

連續型均勻分佈 U(a, b) 的機率密度函數（PDF）在區間 [a, b] 內的值是多少？

A

1

B

1 / (b - a)

C

b - a

D

0

答案解析

連續型均勻分佈 U(a, b) 的 PDF 圖形是一個矩形，其底寬為 (b - a)。為了使 PDF 曲線下方的總面積等於 1（機率公理），矩形的高度（即 PDF 在區間 [a, b] 內的值）必須是 1 / (b - a)。在區間 [a, b] 之外，PDF 的值為 0。

#50

★★

蒙地卡羅方法（Monte Carlo methods）利用什麼來模擬和估計複雜問題的結果？

A

精確的數學公式推導

B

重複進行隨機抽樣（Random Sampling）並利用統計結果

C

邏輯規則推理

D

專家系統知識庫

答案解析

蒙地卡羅方法是一大類計算演算法的總稱，它們依賴於重複的隨機抽樣來獲得數值結果。當一個問題難以透過解析方法（精確公式推導）求解時，蒙地卡羅方法提供了一種基於模擬的近似求解途徑。其基本思想是：對問題涉及的隨機過程進行大量模擬（每次模擬都是一次隨機抽樣），然後根據這些模擬結果的統計特性（如平均值、比例）來估計問題的解。它廣泛應用於物理模擬、金融定價、計算機圖形學、機器學習（如 MCMC - Markov Chain Monte Carlo）等領域。

iPAS AI應用規劃師 經典題庫