iPAS AI應用規劃師 經典題庫
L22101 敘述性統計與資料摘要技術
出題方向
1
統計學基本概念與數據類型
2
集中趨勢量數
3
離散趨勢量數
4
相對位置量數
5
資料分佈形狀
6
敘述統計圖表
7
相關性與關聯分析
8
資料摘要與報表技術
#1
★★★★
敘述性統計(Descriptive Statistics)的主要目的是什麼?
答案解析
統計學主要分為敘述性統計和推論性統計(Inferential
Statistics)。敘述性統計旨在描述和呈現手頭上數據(樣本)的狀況,使用圖表(如直方圖、箱型圖)和數值量數(如平均數、標準差)來總結數據的集中趨勢、離散程度、分佈形狀等基本特徵。它不涉及從樣本推論到母體。選項 B 和 C 屬於推論性統計的範疇。選項 D 屬於預測建模的範疇,雖然可能基於統計原理,但其目的超越了單純的描述。

#2
★★★★★
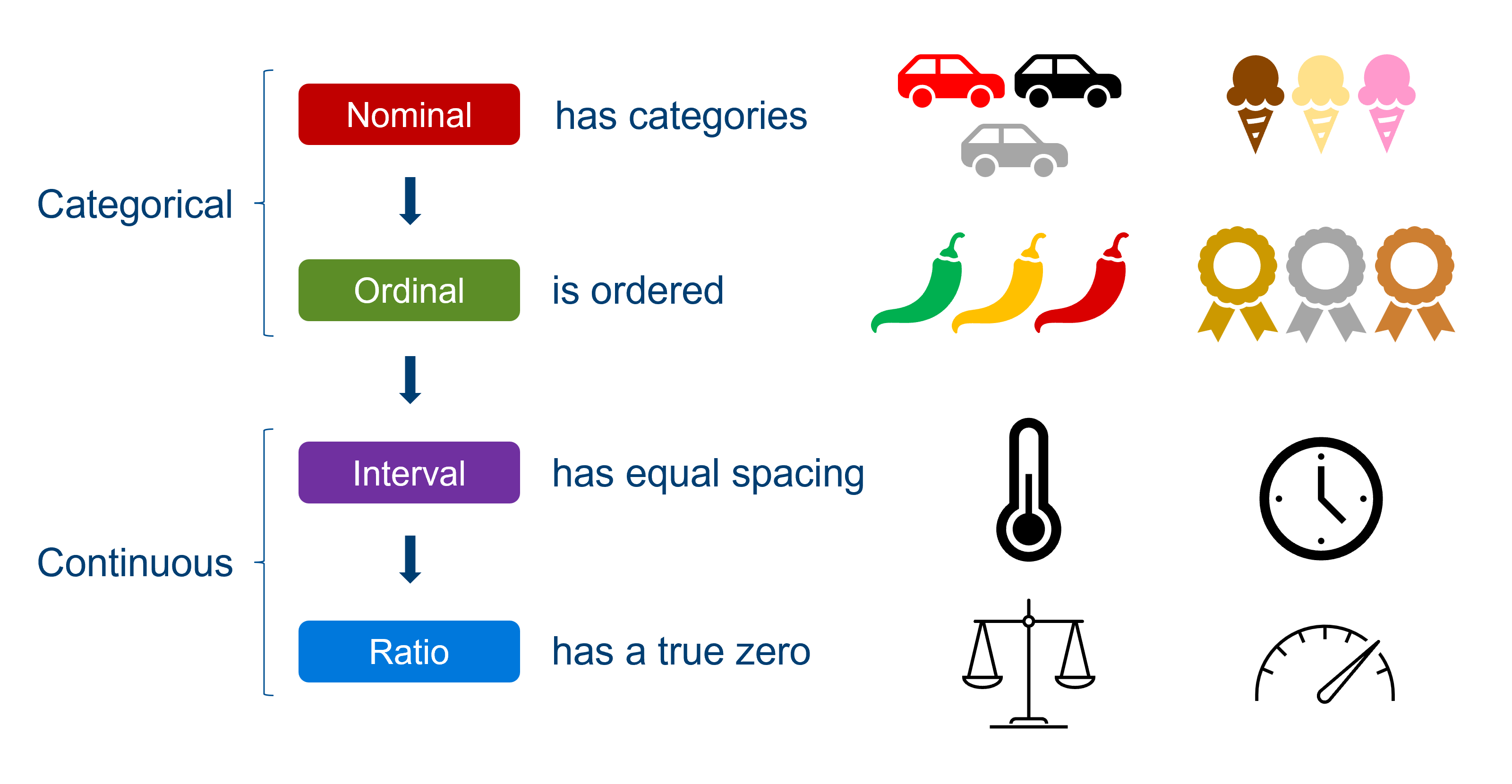
在統計學中,將數據分為名目(Nominal)、次序(Ordinal)、等距(Interval)和等比(Ratio)四種尺度,主要是基於數據的什麼特性?
答案解析
數據的測量尺度決定了數據的性質以及可以對其進行的統計分析類型:
- 名目尺度:僅用於分類,數值無大小或順序意義(如性別、血型)。只能計算次數、眾數。
- 次序尺度:具有順序關係,但差值無意義(如教育程度:國小、國中、高中)。可計算中位數、百分位數。
- 等距尺度:具有順序和相等間距,差值有意義,但沒有絕對零點(如攝氏溫度)。可進行加減運算,計算平均數、標準差。
- 等比尺度:具有等距尺度的所有性質,且有絕對零點,比值有意義(如身高、體重、收入)。可進行所有算術運算。
#3
★★★★★
下列哪一個集中趨勢量數最容易受到極端值(Outliers)的影響?
答案解析
集中趨勢量數用於描述數據的中心位置。
- 平均數:所有數值的總和除以數值個數。因為計算涉及所有數值,所以一個或幾個極端值會顯著拉高或拉低平均數。
- 中位數:將數據排序後位於中間位置的數值。它只取決於數據的位置,不受兩端極端值的影響,因此對異常值具有穩健性(Robust)。
- 眾數:數據中出現次數最多的數值。它也不受極端值的影響,但可能不存在或有多個。
- 幾何平均數:常用於計算比率或增長率的平均,對極端值也較敏感。
#4
★★★★★
標準差(Standard Deviation)是衡量數據的什麼特性?
答案解析
離散趨勢量數用於描述數據的分散或變異程度。標準差是其中最常用的一個指標,它計算的是各數據點與其平均數之間差異的平方的平均數的平方根(即變異數
Variance 的平方根)。標準差越大,表示數據點越分散,偏離平均數的程度越大;標準差越小,表示數據點越集中在平均數附近。選項 A 是集中趨勢。選項 C
是分佈形狀(偏態)。選項 D
是眾數。

#5
★★★★
百分位數(Percentile) P75 代表什麼意義?
答案解析
百分位數是衡量數據相對位置的指標。第 k 個百分位數(Pk)是指一個數值,使得數據集中至少有 k% 的觀測值小於或等於它,同時至少有 (100-k)% 的觀測值大於或等於它。因此,P75(也稱為第三四分位數 Q3)表示數據集中至少有 75% 的數值小於或等於 P75,且至少有 25% 的數值大於或等於 P75。它將數據分成了較低的 75% 和較高的 25%。
#6
★★★★
如果一個數據分佈的偏態係數(Skewness Coefficient)為正值,這通常表示該分佈呈現什麼形狀?
答案解析
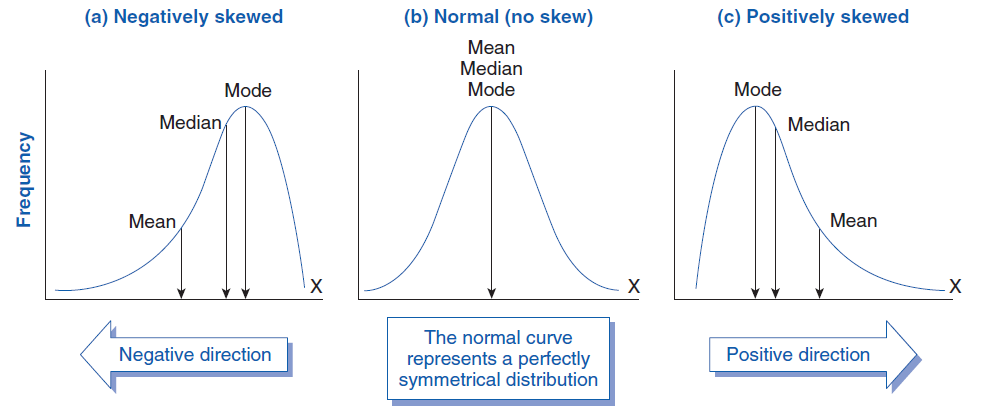
偏態(Skewness)是衡量數據分佈不對稱程度的指標。
- 偏態係數 = 0:表示分佈大致對稱(如常態分佈)。
- 偏態係數 > 0:表示分佈為右偏(或稱正偏),數據的尾部向右側(數值較大的一側)延伸較長,大部分數據集中在左側。在右偏分佈中,通常 平均數 > 中位數 > 眾數。
- 偏態係數 < 0:表示分佈為左偏(或稱負偏),數據的尾部向左側(數值較小的一側)延伸較長,大部分數據集中在右側。在左偏分佈中,通常 平均數 < 中位數 < 眾數。
#7
★★★★★
箱型圖(Box
Plot,或稱盒鬚圖)主要用於呈現數據的哪些統計資訊?
答案解析
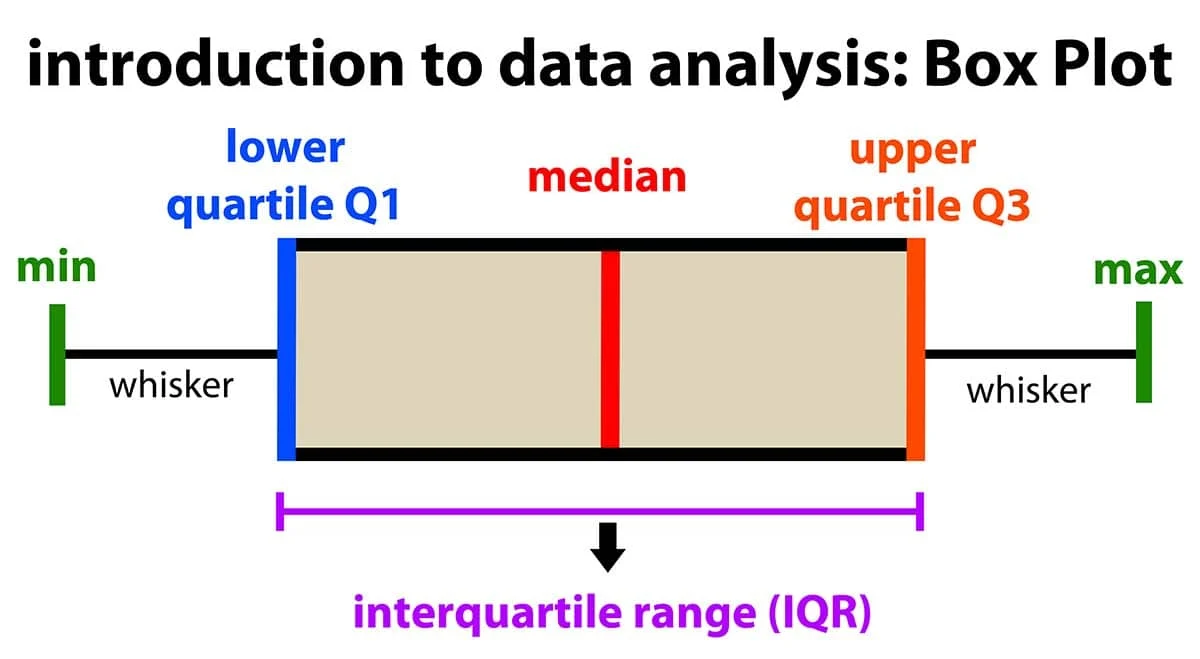
箱型圖是一種有效呈現數據分佈摘要的視覺化圖表。它主要展示了五個關鍵的數值摘要(Five-Number Summary)以及異常值:
- 最小值(Minimum):通常是數據的下邊緣(不含異常值)。
- 第一四分位數(Q1):第 25 百分位數,盒子的下邊緣。
- 中位數(Median, Q2):第 50 百分位數,盒子中間的線。
- 第三四分位數(Q3):第 75 百分位數,盒子的上邊緣。
- 最大值(Maximum):通常是數據的上邊緣(不含異常值)。
#8
★★★★★
皮爾森相關係數(Pearson Correlation Coefficient)主要用於衡量哪種類型變數之間的關係強度與方向?
答案解析
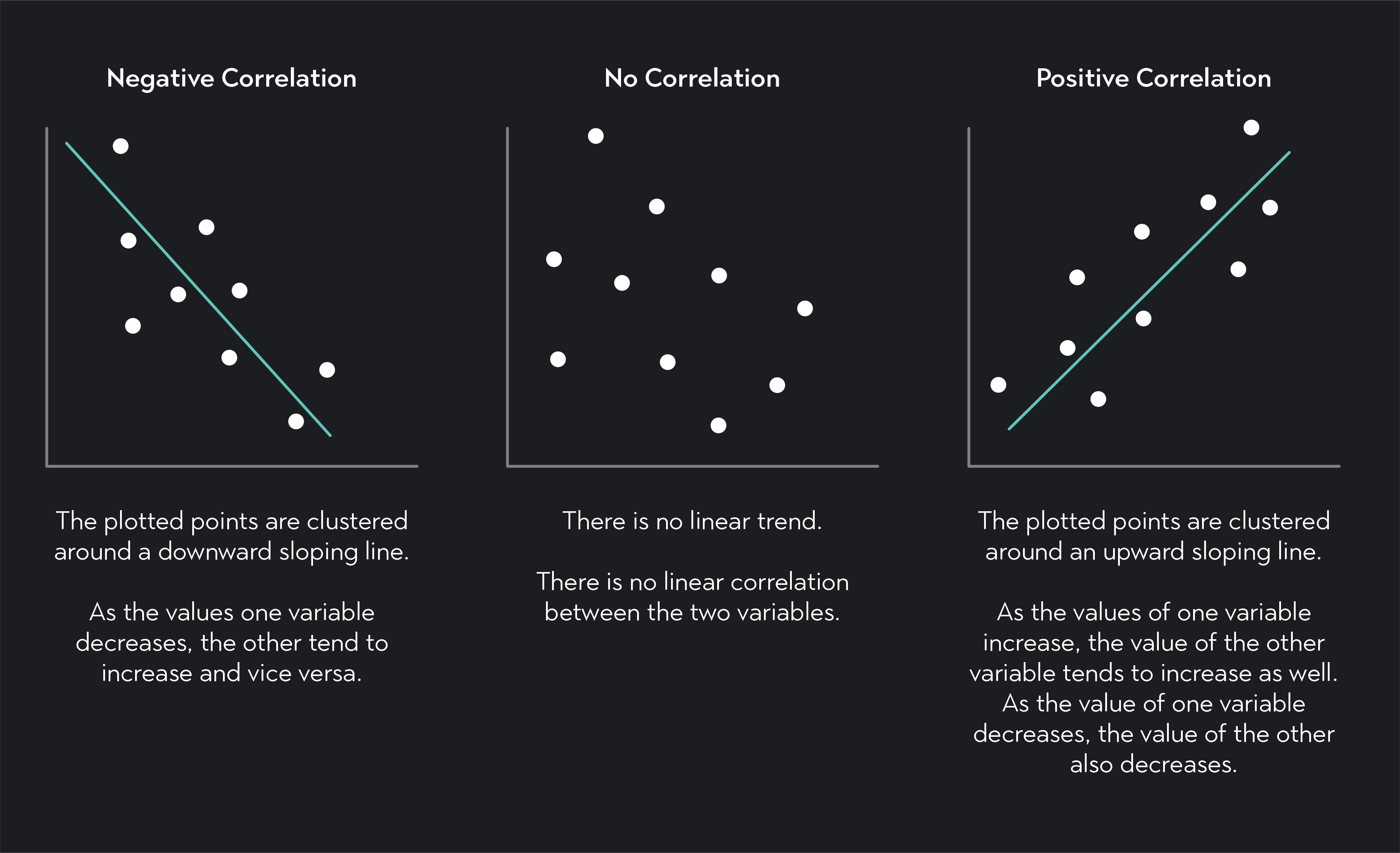
皮爾森相關係數(常用符號 r)是衡量兩個連續變數之間線性關係強度和方向的最常用指標。其值介於 -1 和 +1 之間:
- +1:表示完全正線性相關。
- -1:表示完全負線性相關。
- 0:表示沒有線性相關。
#9
★★★★
四分位距(Interquartile Range, IQR)是如何計算的?它主要用於衡量什麼?
答案解析
四分位距(IQR)是衡量數據離散程度的另一個常用指標,特別是它對異常值不敏感(穩健性)。其計算方法是第三四分位數(Q3,第 75 百分位數)減去第一四分位數(Q1,第 25
百分位數)。IQR 代表了數據集中間
50% 的數值所散佈的範圍。IQR
越大,表示數據中間部分的變異程度越大;IQR 越小,表示數據中間部分越集中。全距(Range)(A)是最大值減最小值,易受極端值影響。選項 C 描述的是常態分佈下的經驗法則。選項 D 是平均數的定義。

#10
★★★★
直方圖(Histogram)與長條圖(Bar Chart)的主要區別在於?
答案解析
雖然兩者都使用長條來表示數據,但用途和繪製方式不同:
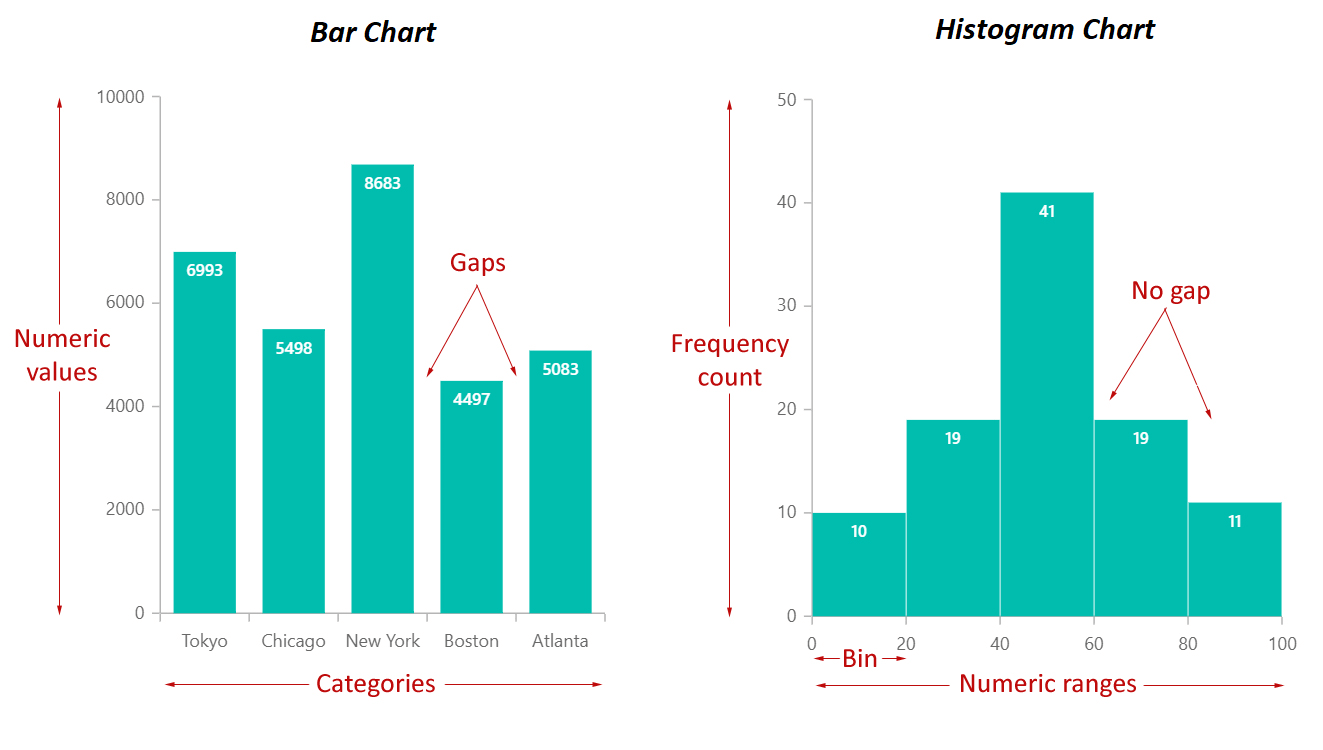
- 直方圖:用於視覺化連續數值型變數的分佈。它將數值範圍劃分成若干個連續的區間(稱為 bins 或組距),然後計算落入每個區間的數據點數量(頻數或頻率),並用長條的高度表示。由於區間是連續的,長條之間通常沒有間隙(除非某區間頻數為零)。
- 長條圖:用於比較離散類別型變數的數量、頻率或某個數值指標。每個長條代表一個獨立的類別,長條的高度表示該類別對應的數值。由於類別是離散的,長條之間通常有間隙以示區分。
#11
★★★★
對於呈現左偏(Left-Skewed)分佈的數據,集中趨勢的典型關係是?
答案解析
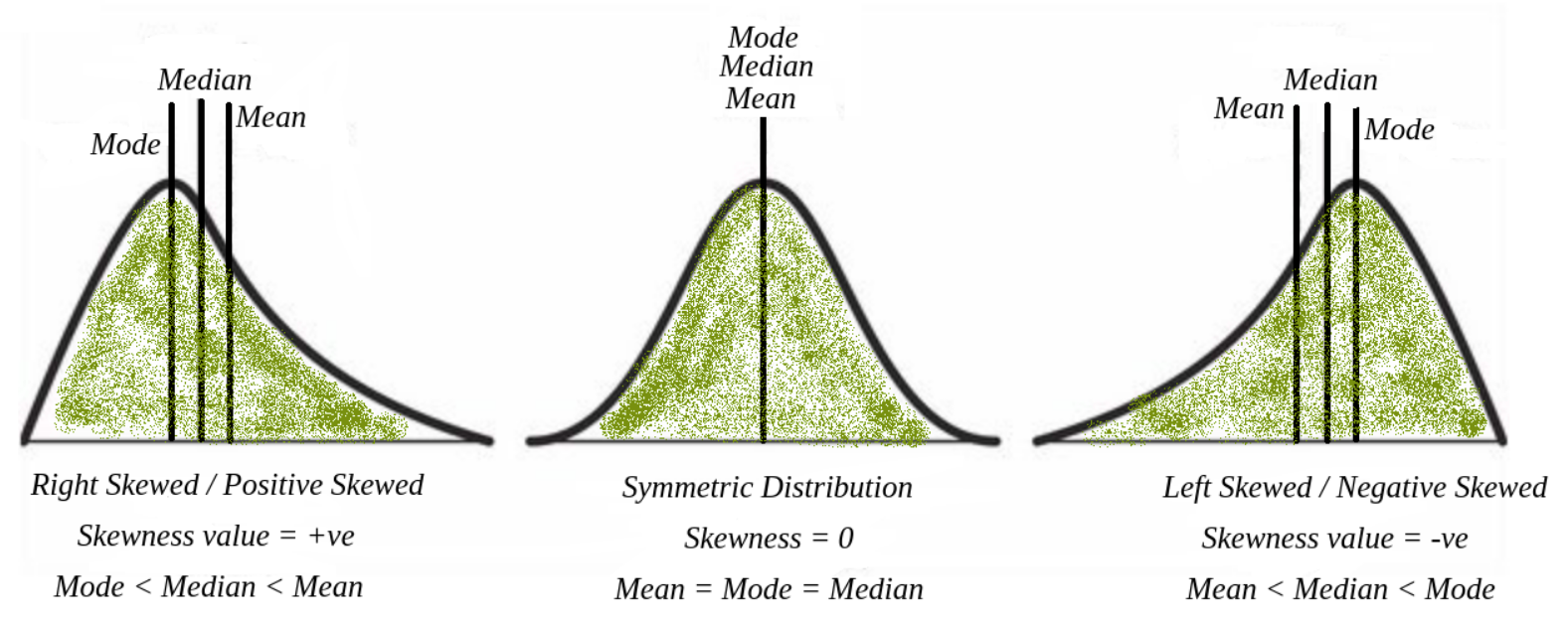
分佈的偏斜度會影響三種集中趨勢量數的相對位置:
- 對稱分佈:平均數 ≈ 中位數 ≈ 眾數。
- 右偏分佈(正偏,尾部向右):少數較大的極端值會將平均數向右拉,因此 平均數 > 中位數 > 眾數。
- 左偏分佈(負偏,尾部向左):少數較小的極端值會將平均數向左拉,因此 平均數 < 中位數 < 眾數。
#12
★★★★
變異係數(Coefficient of Variation, CV)的計算方式及其主要用途是?
答案解析
標準差是一個絕對的離散程度量數,其單位與原始數據相同。當需要比較兩組單位不同(如身高 vs. 體重)或平均數差異很大(如成人身高 vs. 嬰兒身高)的數據的相對變異程度時,直接比較標準差可能沒有意義。變異係數(CV)透過將標準差相對於平均數進行標準化(CV = 標準差 / |平均數|),得到一個無單位的相對離散程度指標。CV 越大,表示數據的相對變異程度越大。例如,可以用 CV 來比較股票 A 的價格波動相對於其平均價格的程度,與股票 B 的價格波動相對於其平均價格的程度。

#13
★★★
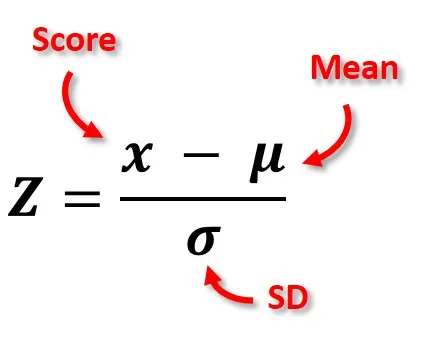
Z 分數(Z-score)的計算公式是 (X - μ) / σ,其中 X 是原始分數,μ 是平均數,σ 是標準差。Z 分數代表什麼意義?
答案解析
Z 分數(也稱為標準分數 Standard
Score)是一種將原始分數轉換為以標準差為單位表示其相對位置的方法。Z
分數的數值表示該原始分數距離其所在數據集的平均數有多少個標準差。Z > 0 表示分數高於平均數,Z
< 0 表示分數低於平均數,Z =
0 表示分數等於平均數。Z
分數的絕對值越大,表示該分數距離平均數越遠。Z 分數常用於:(1) 比較來自不同分佈的分數的相對位置;(2) 偵測異常值(通常 |Z| > 3 被視為異常)。
#14
★★★
峰度(Kurtosis)是衡量數據分佈形態的哪個特性?
答案解析
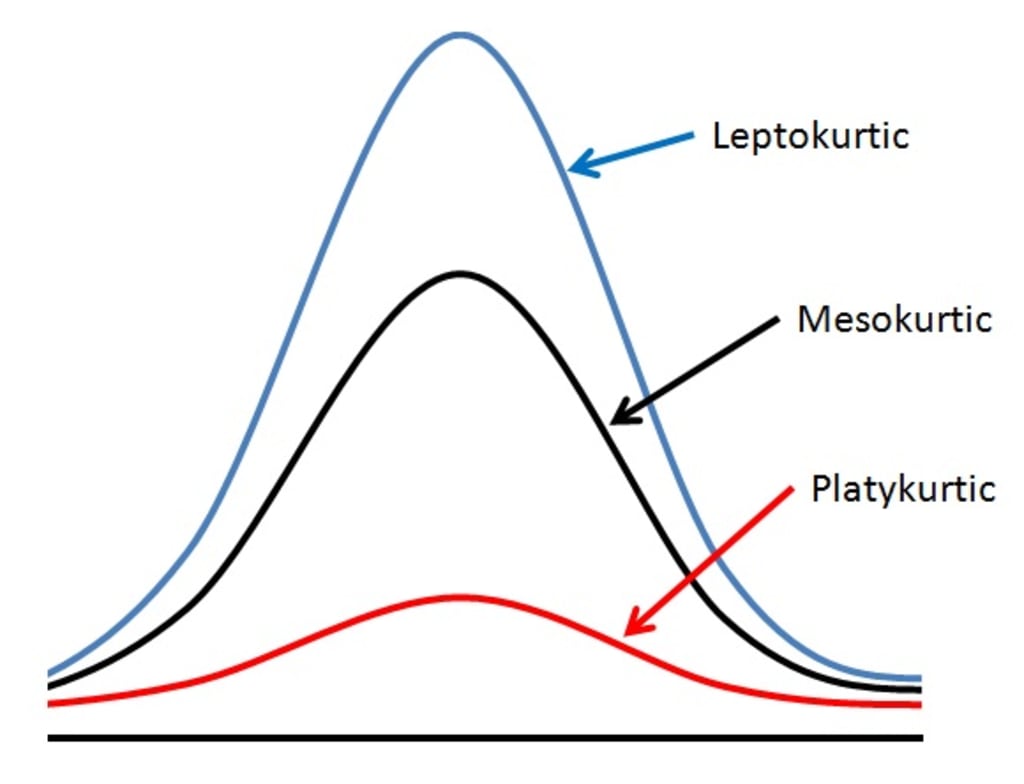
峰度是描述數據分佈形狀的另一個指標(相對於常態分佈)。它主要衡量分佈的峰部是比常態分佈更尖峭還是更平坦,以及尾部是比常態分佈更厚重(包含更多極端值)還是更輕薄。
- 高狹峰(Leptokurtic):峰度值 > 0(相對於常態的超額峰度),峰部更尖,尾部更厚。
- 常態峰(Mesokurtic):峰度值 ≈ 0,與常態分佈相似。
- 低闊峰(Platykurtic):峰度值 < 0,峰部更平坦,尾部更輕薄,極端值較少。

#15
★★★★
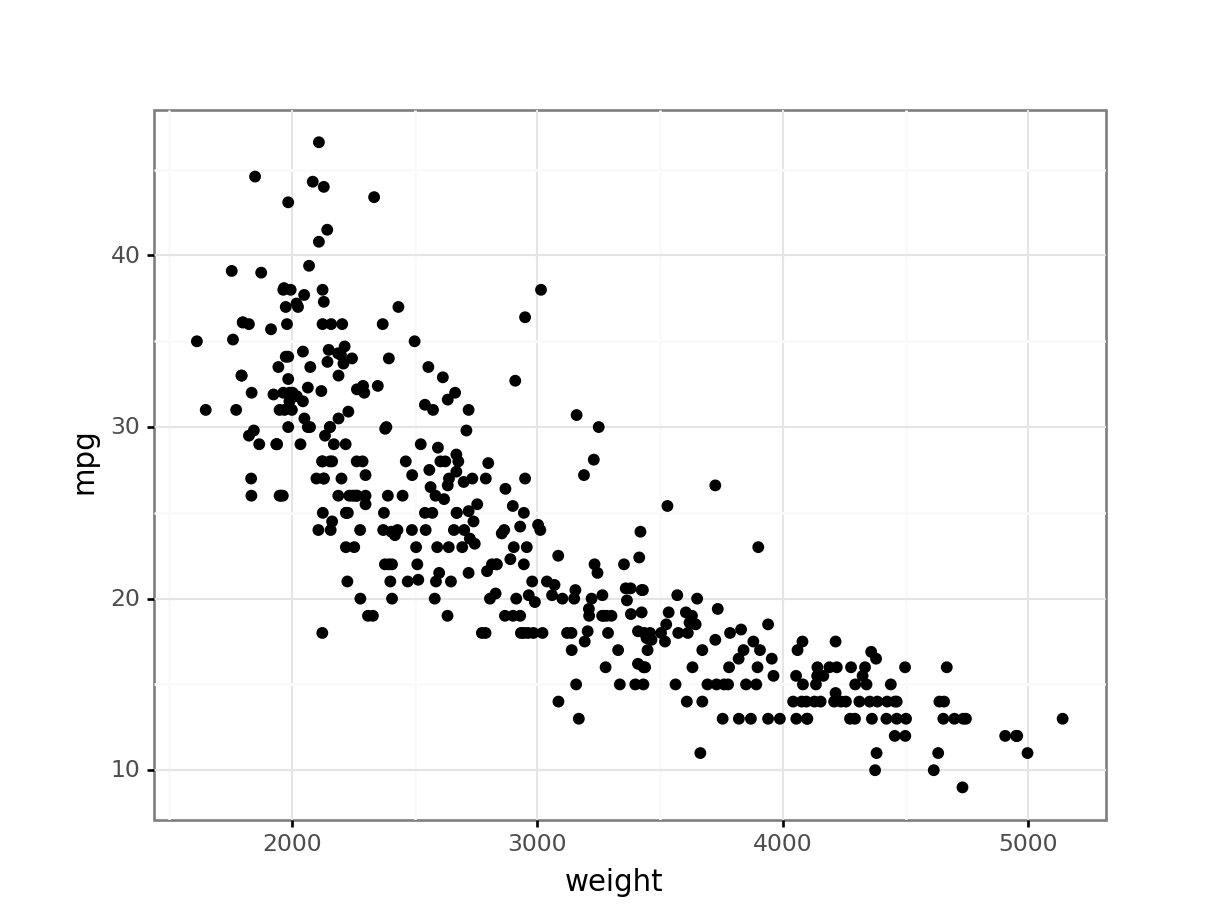
散佈圖(Scatter Plot)最適合用於視覺化探索哪種類型數據之間的關係?
答案解析
散佈圖使用二維笛卡爾座標系,將每個數據點表示為一個點,其中一個數值變數的值對應 X 軸座標,另一個數值變數的值對應 Y 軸座標。透過觀察點的分佈模式,可以直觀地判斷兩個數值變數之間是否存在某種關係(如線性正相關、負相關、非線性關係或無關係),以及關係的強度和是否存在異常點。選項
A 常用長條圖或圓餅圖。選項 C
常用折線圖。選項 D 常用堆疊長條圖或圓餅圖。
#16
★★★★
若兩個變數的皮爾森相關係數為
-0.85,這表示兩者之間存在什麼樣的關係?
答案解析
皮爾森相關係數 r 的值介於 -1 到 +1
之間。符號表示關係的方向:正號表示正相關(一個變數增加,另一個傾向於增加),負號表示負相關(一個變數增加,另一個傾向於減少)。絕對值 |r| 表示線性關係的強度:越接近 1,表示線性關係越強;越接近
0,表示線性關係越弱。r = -0.85,符號為負,表示負相關;絕對值為 0.85,接近 1,表示線性關係強度很強。因此,這表示兩個變數之間存在強度很強的負線性關係。

#17
★★★★
製作資料摘要報告時,針對不同的受眾(如技術團隊 vs.
管理階層),應該注意調整報告的哪個方面?
答案解析
有效的溝通需要考慮受眾的背景和需求。向技術團隊報告時,可以包含更詳細的統計量、模型細節和技術挑戰。但向管理階層或非技術背景的利害關係人報告時,應避免過多的技術術語,著重於呈現關鍵的發現、業務洞察和結論,並多使用易於理解的視覺化圖表(如長條圖、折線圖、儀表板)。報告的重點、詳細程度和呈現方式都需要根據受眾進行調整,以確保資訊能夠被有效接收和理解。數據準確性(A)對所有受眾都很重要。收集時間(C)和軟體版本(D)通常不是報告呈現的主要調整點。
#18
★★★
「請問您的教育程度:(A) 國小 (B) 國中 (C) 高中 (D) 大學 (E) 研究所及以上」,這個問題收集到的數據屬於哪種測量尺度?
答案解析
教育程度的選項之間存在明確的順序關係(研究所 > 大學 > 高中 > ...),因此它不僅僅是名目尺度。然而,我們不能說「大學」和「高中」之間的差距與「國中」和「國小」之間的差距是相等的(差值無意義),也不存在絕對的零點。因此,這種數據屬於次序尺度。

#19
★★★
計算一組數據 {2, 3, 3, 4, 5, 8, 10} 的中位數(Median)是多少?
答案解析
計算中位數的步驟:
- 將數據從小到大排序:{2, 3, 3, 4, 5, 8, 10}
- 找出位於中間位置的數值。這組數據有 7 個數值(奇數個),中間位置是第 (7+1)/2 = 4 個數值。
- 第 4 個數值是 4。
#20
★★★
變異數(Variance)的計算涉及到每個數據點與平均數差異的平方和。如果所有數據點都完全相同,則變異數為多少?
答案解析
變異數衡量數據的離散程度。如果所有數據點都完全相同,那麼每個數據點都等於平均數。因此,每個數據點與平均數的差異都是
0。這些差異的平方和自然也是 0,所以變異數為 0。這表示數據沒有任何變異或分散。

#21
★★★
某次考試中,小明的 Z 分數為 1.5,小華的 Z 分數為 -0.5。這表示?
答案解析
Z 分數表示一個分數距離平均數有多少個標準差。正的 Z 分數表示該分數高於平均數,負的 Z
分數表示該分數低於平均數。小明的 Z 分數為 1.5(正數),表示他的分數高於平均數 1.5 個標準差。小華的 Z 分數為 -0.5(負數),表示他的分數低於平均數 0.5 個標準差。因此,小明的表現相對較好,高於平均;小華的表現相對較差,低於平均。

#22
★★★
峰度係數(Kurtosis Coefficient)可以用來比較數據分佈尾部的厚重程度。哪個分佈的尾部最厚重(包含更多極端值)?
答案解析
如前所述,峰度衡量峰部尖峭度和尾部厚重度。高狹峰(Leptokurtic)分佈的特點是峰部比常態分佈更尖,同時尾部比常態分佈更厚,這意味著出現極端值的機率相對較高。常態峰(Mesokurtic)是基準。低闊峰(Platykurtic)則是峰部較平坦,尾部較輕薄,極端值較少。因此,高狹峰分佈的尾部最厚重。


#23
★★★
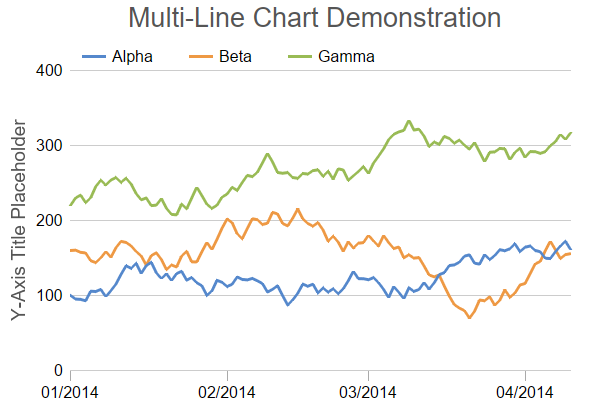
想要視覺化比較不同產品線在過去一年中每個月的銷售額變化趨勢,最適合使用哪種圖表?
答案解析
折線圖特別適合用於展示數據隨時間變化的趨勢。當需要比較多個類別(如不同產品線)在同一時間維度上的趨勢時,可以使用多線折線圖,每一條線代表一個產品線,X 軸表示時間(月份),Y
軸表示銷售額。這樣可以清晰地比較各產品線的銷售表現及其隨時間的波動情況。圓餅圖(A)適用於顯示各部分佔整體的比例。散佈圖(B)適用於觀察兩個數值變數的關係。箱型圖(D)適用於展示數據分佈的摘要。
#24
★★★
如果兩個變數的相關係數接近於 0,這表示?
答案解析
皮爾森相關係數衡量的是線性關係的強度和方向。相關係數接近 0 僅表示兩個變數之間缺乏線性關係。然而,它們之間可能存在其他類型的關係,例如二次方關係(呈現 U 型或倒 U
型)、週期性關係或其他複雜的非線性模式。因此,不能斷定它們之間沒有任何關係。觀察散佈圖是判斷是否存在非線性關係的更好方法。

#25
★★★
在製作資料摘要報告時,設計的首要原則應該是?
答案解析
儀表板的目的是將關鍵資訊和指標以易於理解和監控的方式呈現給使用者(通常是決策者)。有效的儀表板設計應遵循以下原則:(1)
明確目標受眾和目的:了解誰會使用儀表板以及他們需要回答什麼問題。(2)
聚焦關鍵指標:突出顯示最重要的 KPI 和核心洞察,避免資訊過載。(3) 選擇合適的視覺化:根據數據類型和要傳達的訊息選擇最清晰的圖表。(4) 保持簡潔和直觀:佈局清晰,易於瀏覽和理解。(5) 提供上下文:例如與目標值或歷史數據進行比較。選項 B 涵蓋了最重要的原則。選項 A 和 C
可能導致混亂和失焦。選項 D 則失去了儀表板的摘要和視覺化價值。
#26
★★
下列何者屬於類別型(Categorical)數據?
答案解析
類別型數據是將觀測值歸入不同組別或類別的數據。顧客的居住城市(如台北、台中、高雄)是將顧客歸入不同地理類別,屬於類別型數據(更具體地說是名目尺度)。顧客年齡(A)、年收入(C)和上次購買距今天數(D)都是可以進行數學運算的數值,屬於數值型(Numerical)或稱定量(Quantitative)數據(通常是等比尺度)。

#27
★★★
當數據呈現高度右偏(Positively Skewed)時,哪個集中趨勢量數通常會小於平均數?
答案解析
在高度右偏的分佈中,存在少數數值很大的極端值,這些極端值會將平均數往右邊(數值較大方向)拉。而中位數只受數據位置影響,眾數是出現次數最多的值(通常在數據密集的區域),它們受極端值的影響較小。因此,在典型的右偏分佈中,量數的關係是:平均數 > 中位數 > 眾數。所以,中位數和眾數通常都會小於平均數。

#28
★★★
全距(Range)作為離散趨勢量數的主要缺點是?
答案解析
全距的計算非常簡單(最大值 - 最小值)(A
錯誤)。然而,它只考慮了數據的兩個端點值,完全忽略了數據集中間部分的分布情況。如果數據中存在一個或兩個極端值,全距就會被這些極端值決定,無法真實反映數據整體的離散程度,因此它是一個非常不穩健(Non-robust)的離散趨勢量數(B
正確)。全距適用於數值型數據(C
錯誤),其單位與原始數據相同(D 錯誤)。

#29
★★
四分位數(Quartiles)將排序後的數據分成幾個相等的部分?
答案解析
四分位數是將排序後的數據集分成四個包含相等數量(約 25%)數據點的部分的分割點。這三個分割點分別是:
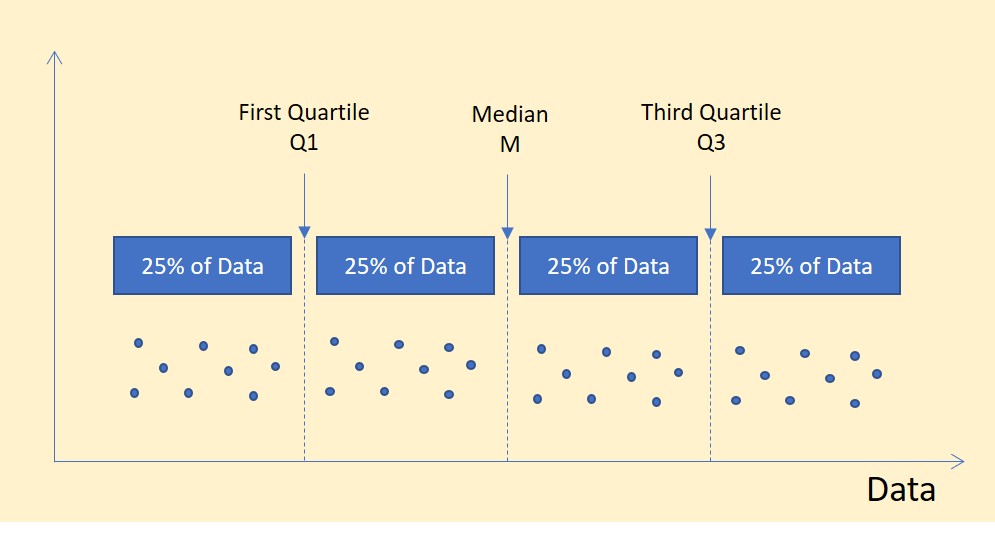
- 第一四分位數 (Q1):第 25 百分位數。
- 第二四分位數 (Q2):第 50 百分位數,也就是中位數。
- 第三四分位數 (Q3):第 75 百分位數。

#30
★★
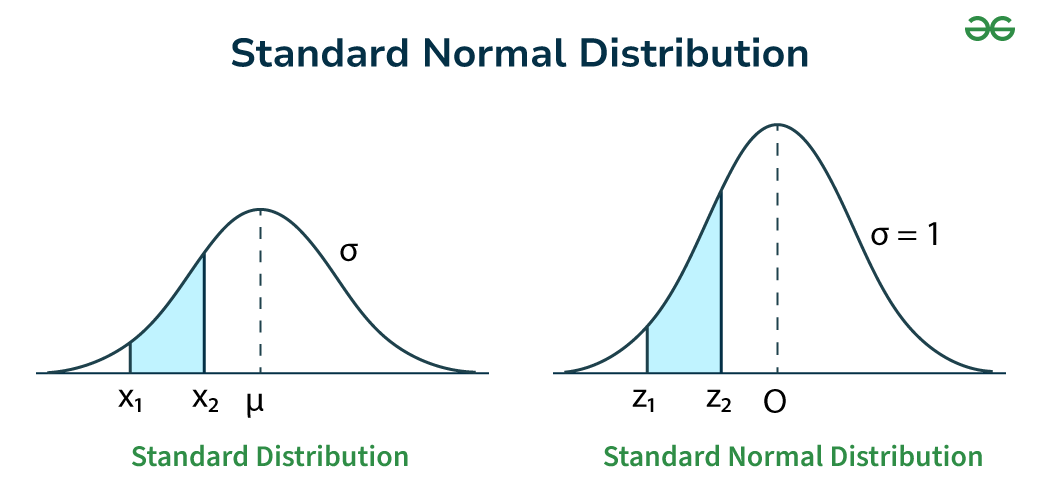
常態分佈(Normal Distribution)曲線的形狀特徵是?
答案解析
常態分佈(也稱高斯分佈 Gaussian
Distribution)是統計學中最重要的一種機率分佈。其機率密度函數曲線呈現對稱的鐘形,峰值位於平均數處。在常態分佈中,平均數、中位數和眾數三者相等。其偏態係數為
0,超額峰度係數也為 0。許多自然和社會現象中的變數分佈都近似於常態分佈。
#31
★★★
圓餅圖(Pie
Chart)最適合用來呈現哪種類型的數據資訊?
答案解析
圓餅圖將一個圓形(代表總體
100%)分割成多個扇形,每個扇形的角度(或面積)代表其對應類別佔總體的比例或百分比。它非常直觀地展示了各部分相對於整體的構成情況。然而,當類別過多或各類別比例相近時,圓餅圖可能難以準確比較各部分的大小,此時長條圖可能是更好的選擇。選項 A 適用折線圖,選項 C 適用散佈圖,選項 D 適用直方圖或箱型圖。
#32
★★★
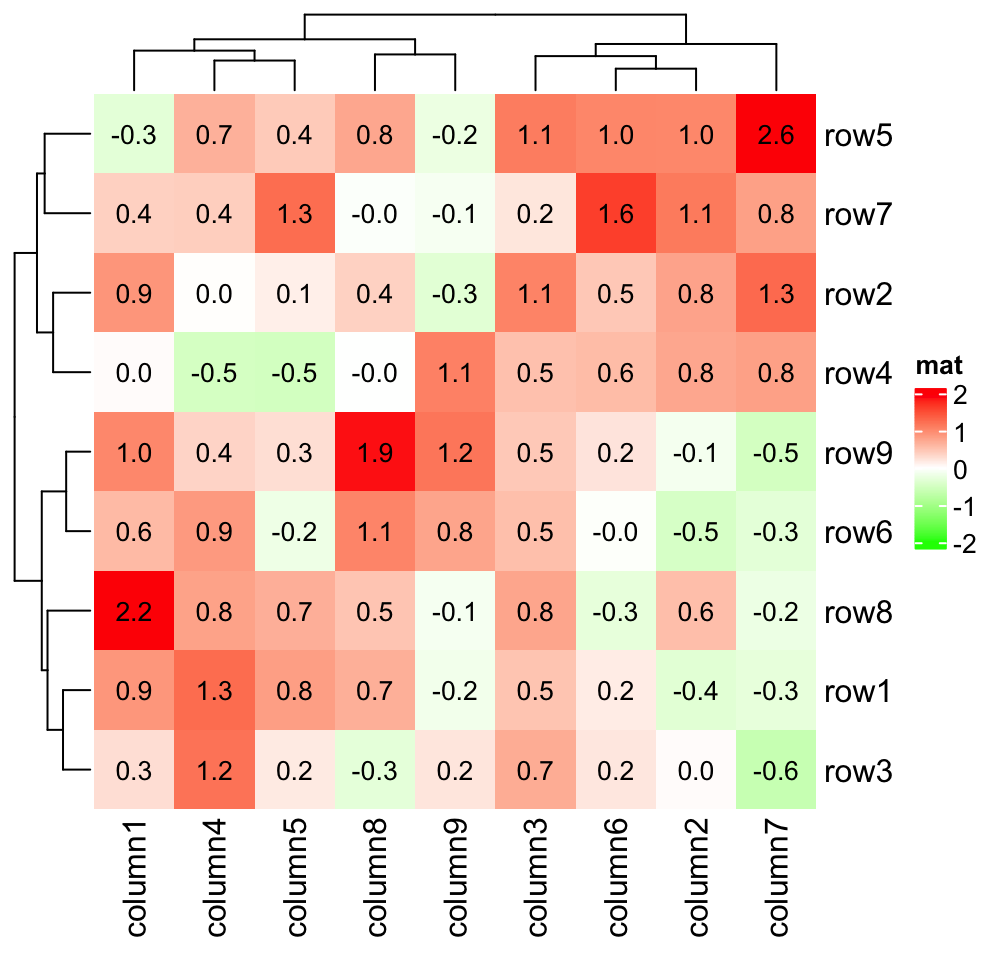
熱力圖(Heatmap)在資料分析中常用於視覺化呈現什麼資訊?
答案解析
熱力圖是一種將矩陣數據視覺化的方法。它使用不同的顏色或顏色強度來表示矩陣中每個單元格的數值大小。顏色越深(或越暖色調)通常表示數值越大,反之則越小。熱力圖常用於:(1) 視覺化相關係數矩陣:快速識別哪些變數之間存在強相關性。(2) 展示混淆矩陣:清晰顯示分類模型的預測情況。(3) 比較不同類別在多個指標上的表現。(4) 基因表達數據分析等。選項 D
地理空間數據通常用地圖視覺化呈現。
#33
★★★
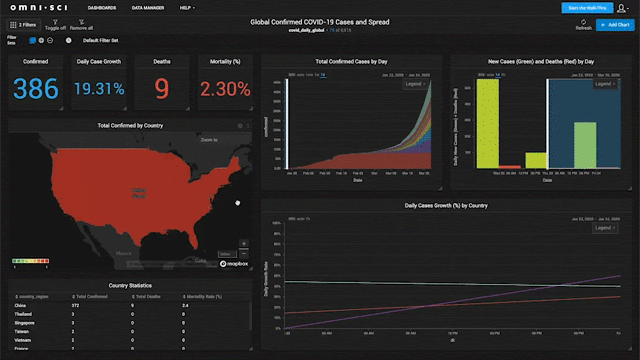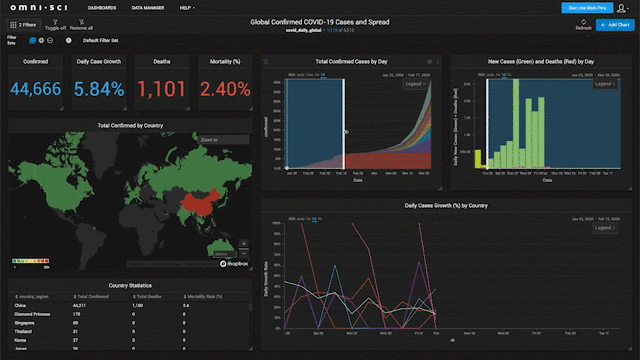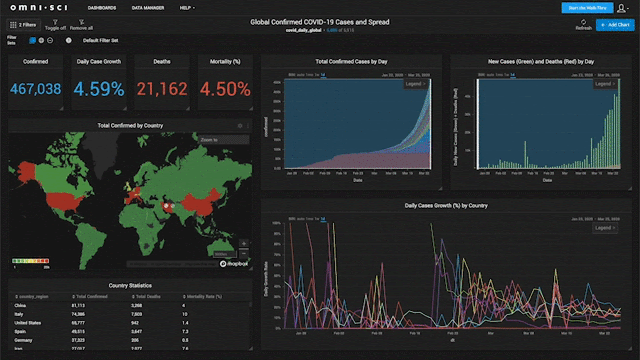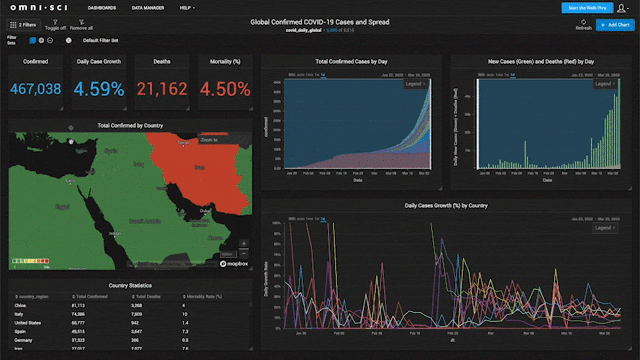
互動式資料視覺化(Interactive Data Visualization)相比於靜態圖表的主要優勢是?
答案解析
靜態圖表只能呈現固定的視圖,而互動式視覺化(常見於網頁儀表板或 BI
工具)允許使用者與圖表進行互動。例如,使用者可以:(1) 縮放(Zooming):放大感興趣的區域。(2) 篩選(Filtering):只顯示特定條件下的數據。(3) 懸停(Hovering):將滑鼠移到數據點上顯示詳細資訊。(4) 點擊(Clicking):觸發下鑽(Drill-down)或聯動其他圖表。這種互動性使得使用者能夠更主動、更深入地探索數據,發現靜態圖表可能忽略的細節和模式,從而獲得更豐富的洞察。製作成本(A)通常更高。選項
C、D 顯然不正確。
#34
★★★
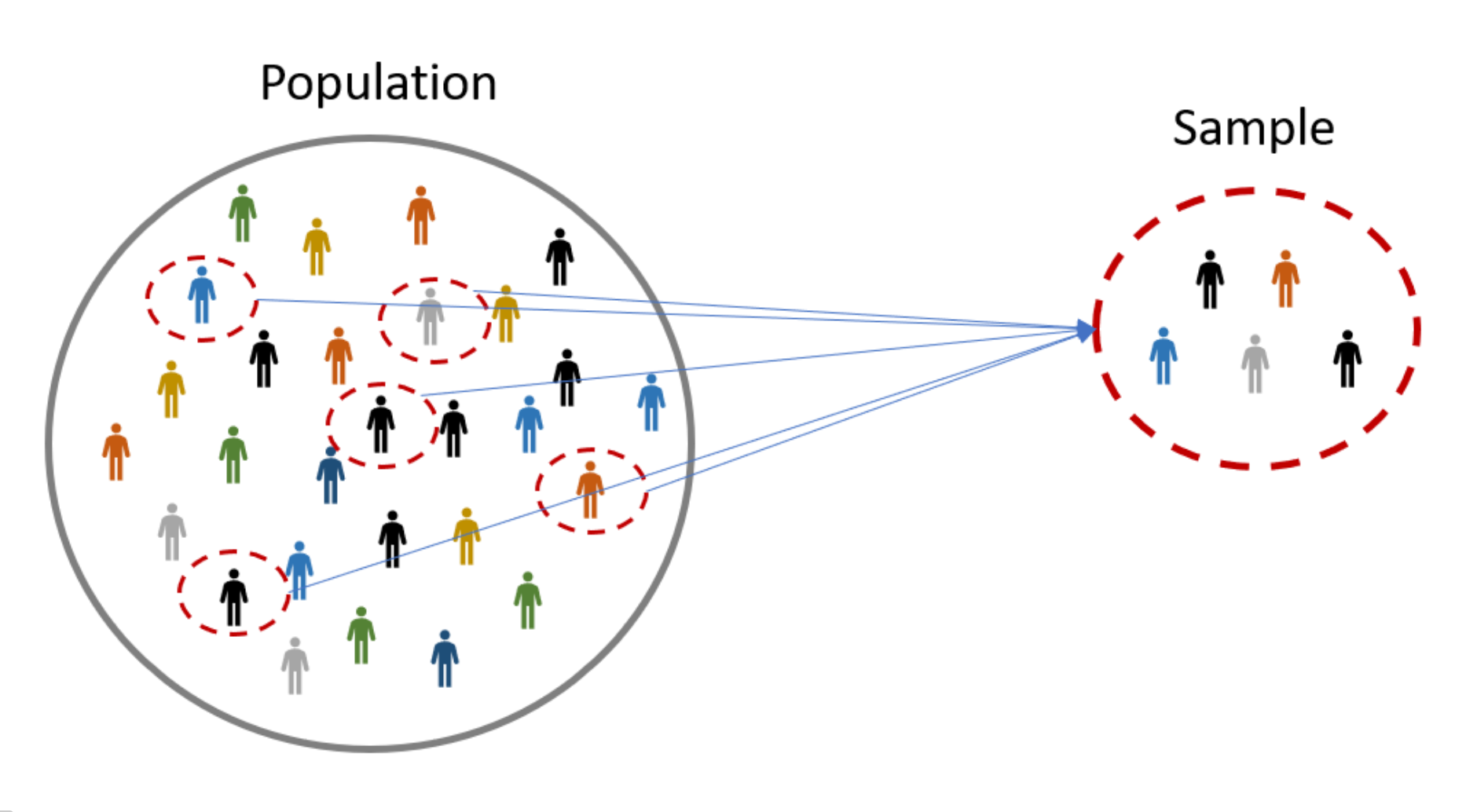
母體(Population)與樣本(Sample)的關係是?
答案解析
在統計學中,母體是指研究者感興趣的所有個體或觀測值的完整集合(例如,全台灣所有大學生的身高)。由於研究整個母體往往不切實際(成本高、耗時長),研究者通常會從母體中抽取一部分具有代表性的個體或觀測值,這個子集就稱為樣本(例如,隨機抽取 1000 名台灣大學生的身高)。敘述性統計描述的是樣本的特徵,而推論性統計則是利用樣本的資訊來推斷或估計母體的特徵(如母體平均身高)。樣本是母體的一部分,樣本量通常遠小於母體量。
#35
★★★
如果一組數據的標準差為 0,這意味著什麼?
答案解析
標準差衡量數據相對於平均數的離散程度。標準差的計算涉及每個數據點與平均數差異的平方和。只有當所有數據點都與平均數完全相等時,這些差異才會全部為 0,導致標準差為 0。因此,標準差為 0
意味著數據沒有任何變異,所有觀測值都是同一個數值。這與數據是否呈常態分佈(A)、是否存在極端值(B)或平均數是否為
0(D)沒有必然聯繫。

#36
★★★
第一四分位數(Q1)與第 25 百分位數(P25)的關係是?
答案解析
四分位數是百分位數的特殊情況。第一四分位數(Q1)定義為將數據從小到大排序後,排在第 25% 位置的數值,也就是第 25 百分位數(P25)。同理,第二四分位數(Q2)等於第 50 百分位數(P50,即中位數),第三四分位數(Q3)等於第 75
百分位數(P75)。

#37
★★★
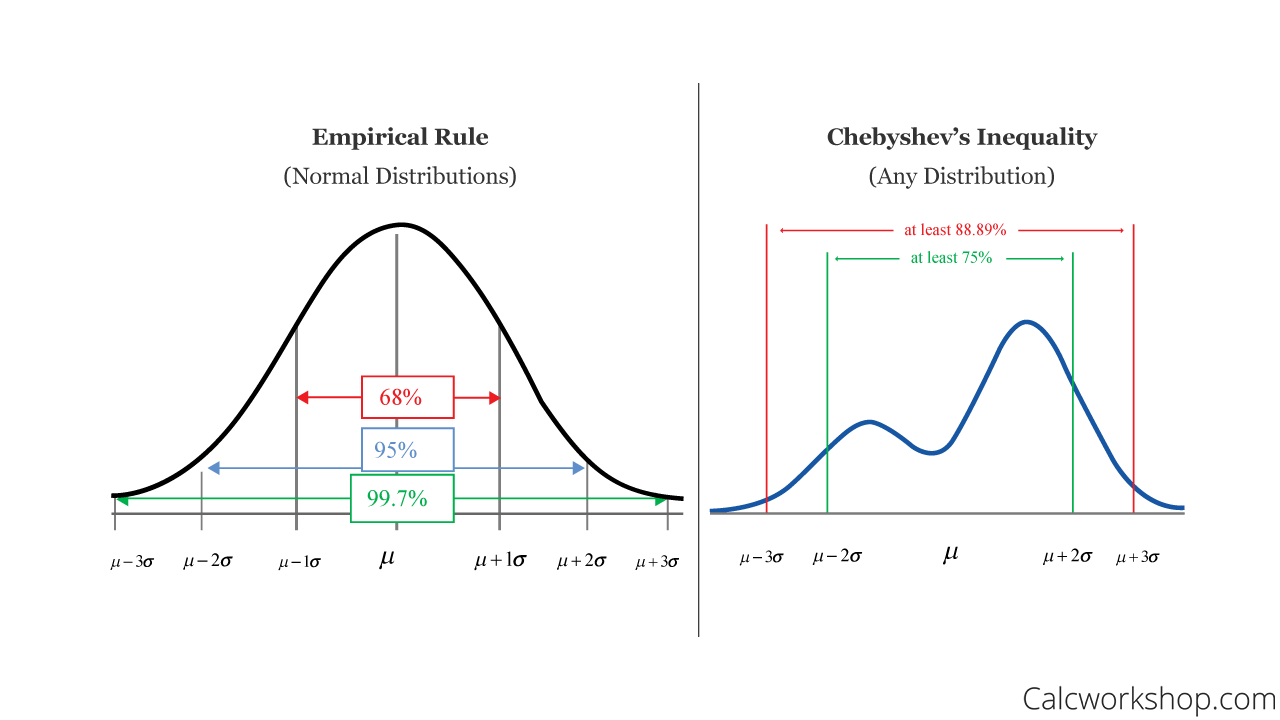
柴比雪夫不等式(Chebyshev's Inequality)提供了一個關於數據分佈的什麼樣的資訊?
答案解析
柴比雪夫不等式是一個普遍適用於任何機率分佈(無論其形狀如何)的定理。它說明,對於任何 k > 1,至少有 (1 - 1/k^2) 比例的數據會落在距離平均數 k 個標準差的範圍 [μ - kσ, μ
+ kσ] 之內。例如,當 k=2 時,至少有 (1 - 1/2^2) = 3/4 = 75% 的數據落在平均數
±2 個標準差內;當 k=3 時,至少有 (1 - 1/3^2) = 8/9 ≈ 88.9%
的數據落在平均數 ±3 個標準差內。相較於只適用於常態分佈的經驗法則(68-95-99.7 法則),柴比雪夫不等式提供了一個更保守但適用範圍更廣的下限保證。
#38
★★★
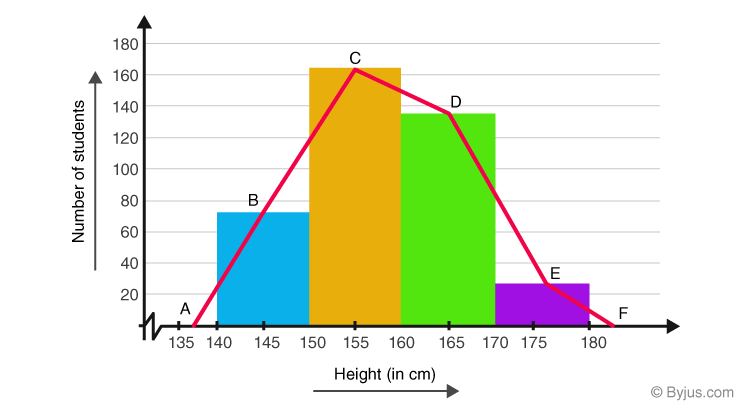
頻率多邊形圖(Frequency Polygon)通常是如何繪製的?
答案解析
頻率多邊形圖是另一種視覺化連續數值數據分佈的方法,可以看作是直方圖的一種變形。它的繪製方法是:先確定直方圖的各個組距(bins),找到每個組距的中點,然後以該中點為橫座標,以該組距的頻數(或頻率)為縱座標標出點,最後用直線依次連接這些點。通常還會在第一個組距左側和最後一個組距右側各增加一個頻數為零的點,使得多邊形圖的兩端能落到橫軸上,形成一個封閉的多邊形。它比直方圖更能清晰地展示分佈的形狀和趨勢。
#39
★★★★
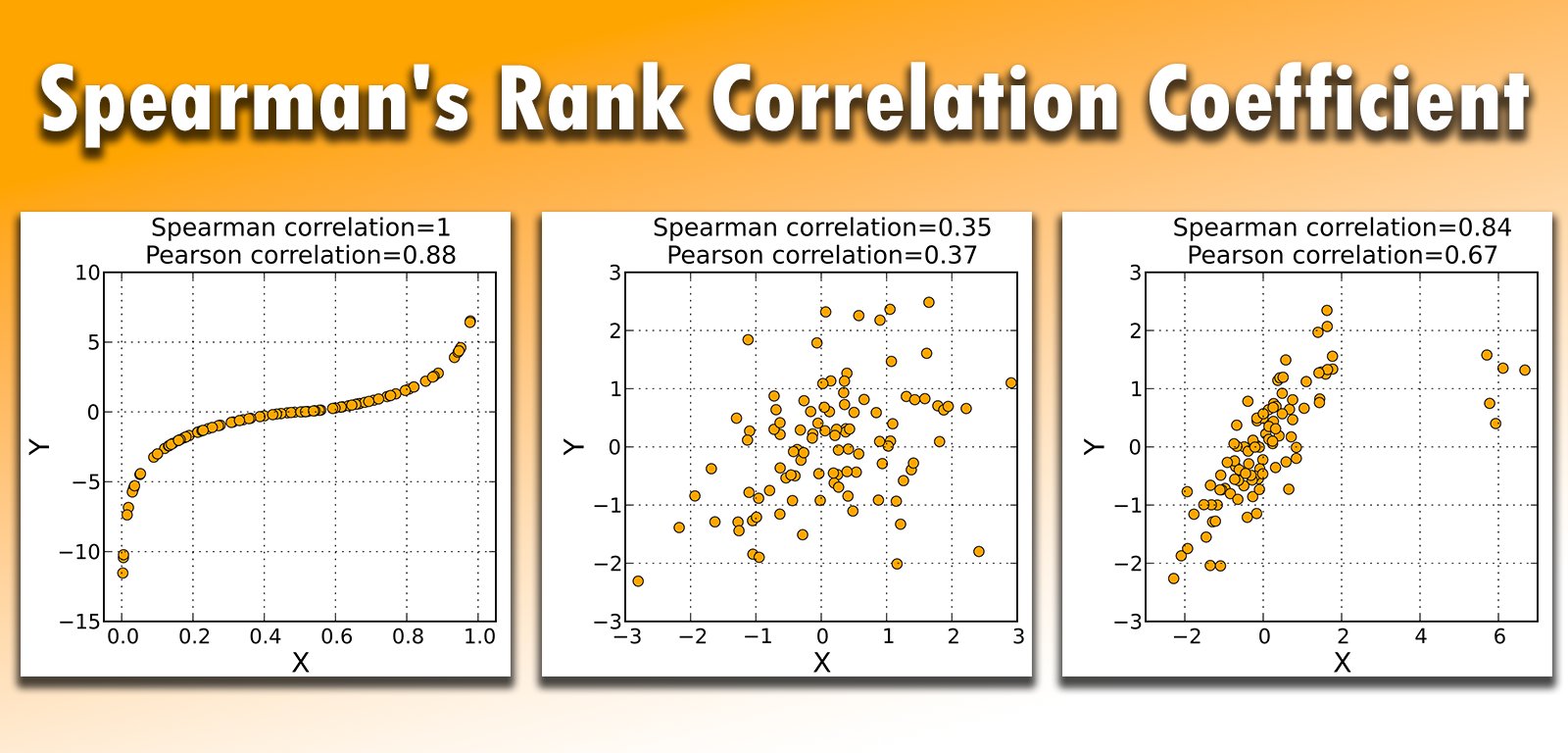
斯皮爾曼等級相關係數(Spearman Rank Correlation Coefficient)與皮爾森相關係數的主要不同之處在於?
答案解析
斯皮爾曼等級相關係數(常用符號 ρ 或
rs)是一種非參數的相關性度量。它不直接使用原始數據值,而是先將兩個變數的數據分別轉換為它們的等級(排序位置),然後計算這些等級之間的皮爾森相關係數。因此,它衡量的是兩個變數之間單調關係的強度和方向(即一個變數增加時,另一個變數是傾向於增加還是減少,而不要求其關係必須是直線)。主要優點是:(1)
適用於次序尺度數據;(2) 對異常值不敏感(因為使用的是等級);(3) 能捕捉到非線性的單調關係。其值域也是 -1 到 +1(C 錯誤)。選項 A 錯誤。選項 D
錯誤,斯皮爾曼對異常值較不敏感。
#40
★★★
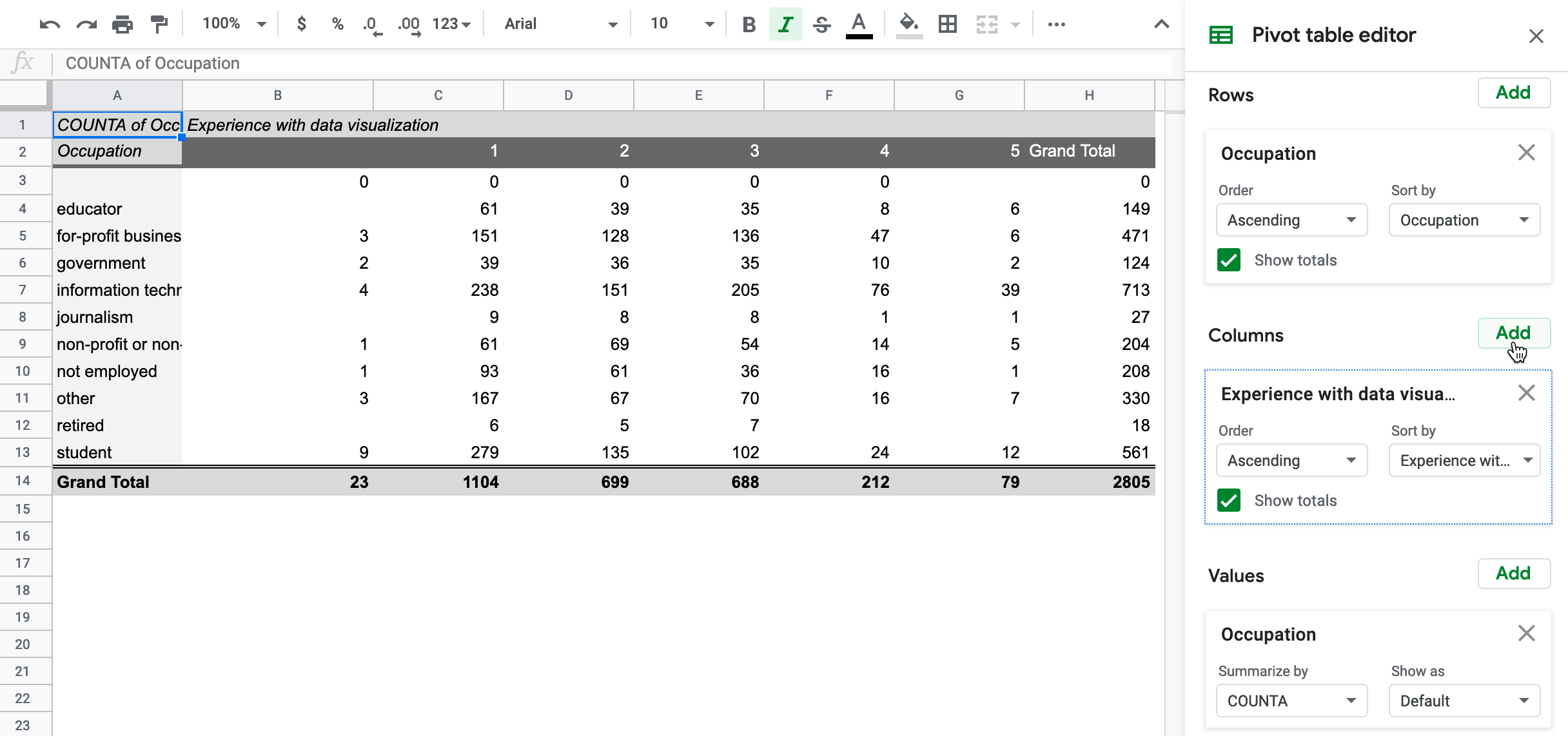
在資料摘要技術中,樞紐分析表(Pivot Table)的主要功能是?
答案解析
樞紐分析表是電子試算表軟體(如 Excel)和數據分析工具中常用的一種強大功能。它允許使用者選擇原始表格數據中的欄位,將它們拖放到不同的區域(如列、欄、值、篩選器),從而動態地、交互地對數據進行重新組織和匯總計算。使用者可以輕鬆地按不同維度進行分組、計算總計、平均值、計數等聚合指標,快速地從不同角度探索和摘要大量數據,是進行探索性分析和製作摘要報表的有效工具。
#41
★★
離散型變數(Discrete Variable)和連續型變數(Continuous
Variable)的主要區別是?
答案解析
數值型變數可以進一步分為離散型和連續型:
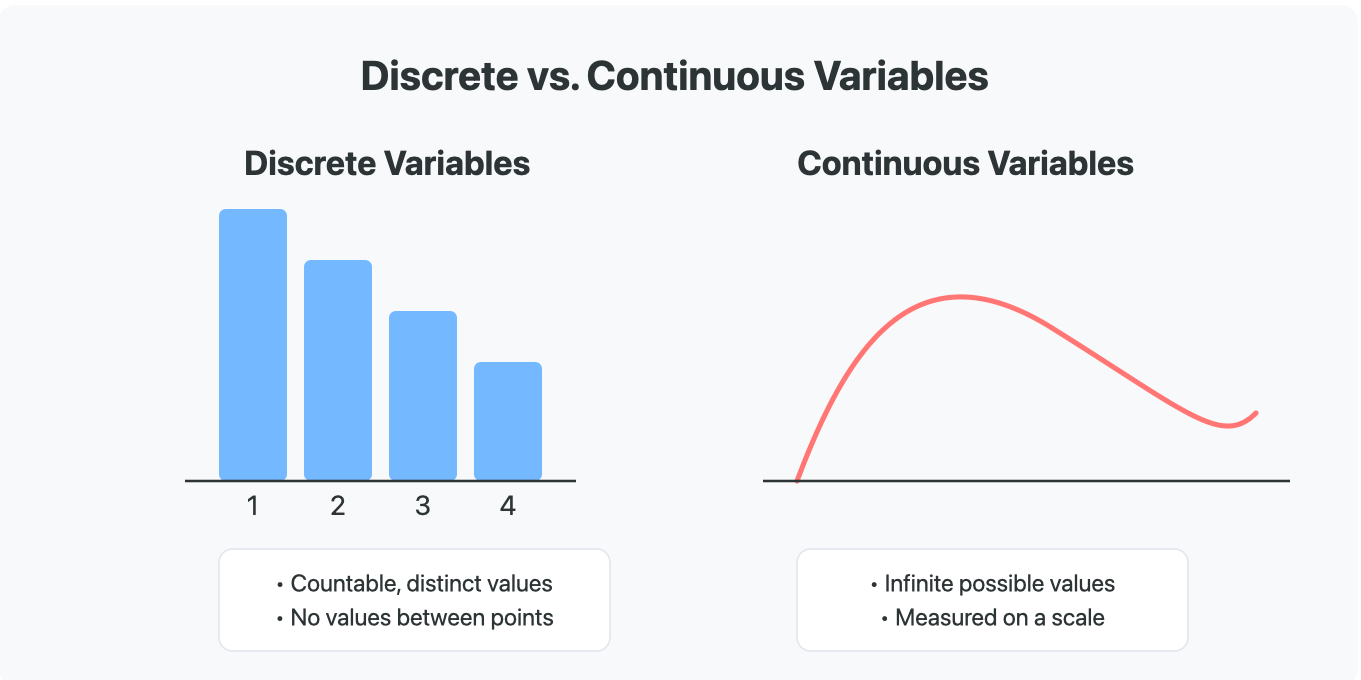
- 離散型變數:其可能取的值是孤立的、可數的點。例如,一個家庭的孩子數量(0, 1, 2, ...)、投擲骰子的點數(1, 2, 3, 4, 5, 6)、每小時通過某路口的汽車數量。即使可能取的值有無限多個(如泊松分佈),但值之間是跳躍的。
- 連續型變數:其可能取的值可以在一個給定的範圍內連續變化,任意兩個值之間都可能存在其他值。例如,身高、體重、溫度、時間。

#42
★★
下列哪個量數不是衡量數據離散程度的指標?
答案解析
離散趨勢量數用於描述數據點相互之間的分散程度或偏離中心位置的程度。常見的離散趨勢量數包括全距、變異數、標準差、四分位距、平均絕對離差等。眾數是衡量數據集中趨勢的指標,表示數據中出現次數最多的值,它不反映數據的分散情況。
#43
★★
如果數據分佈非常對稱,其偏態係數(Skewness Coefficient)應接近於多少?
答案解析
偏態係數衡量數據分佈的不對稱程度。對於完全對稱的分佈(如常態分佈),其偏態係數為 0。正值表示右偏,負值表示左偏。絕對值越大,表示偏斜程度越嚴重。

#44
★★
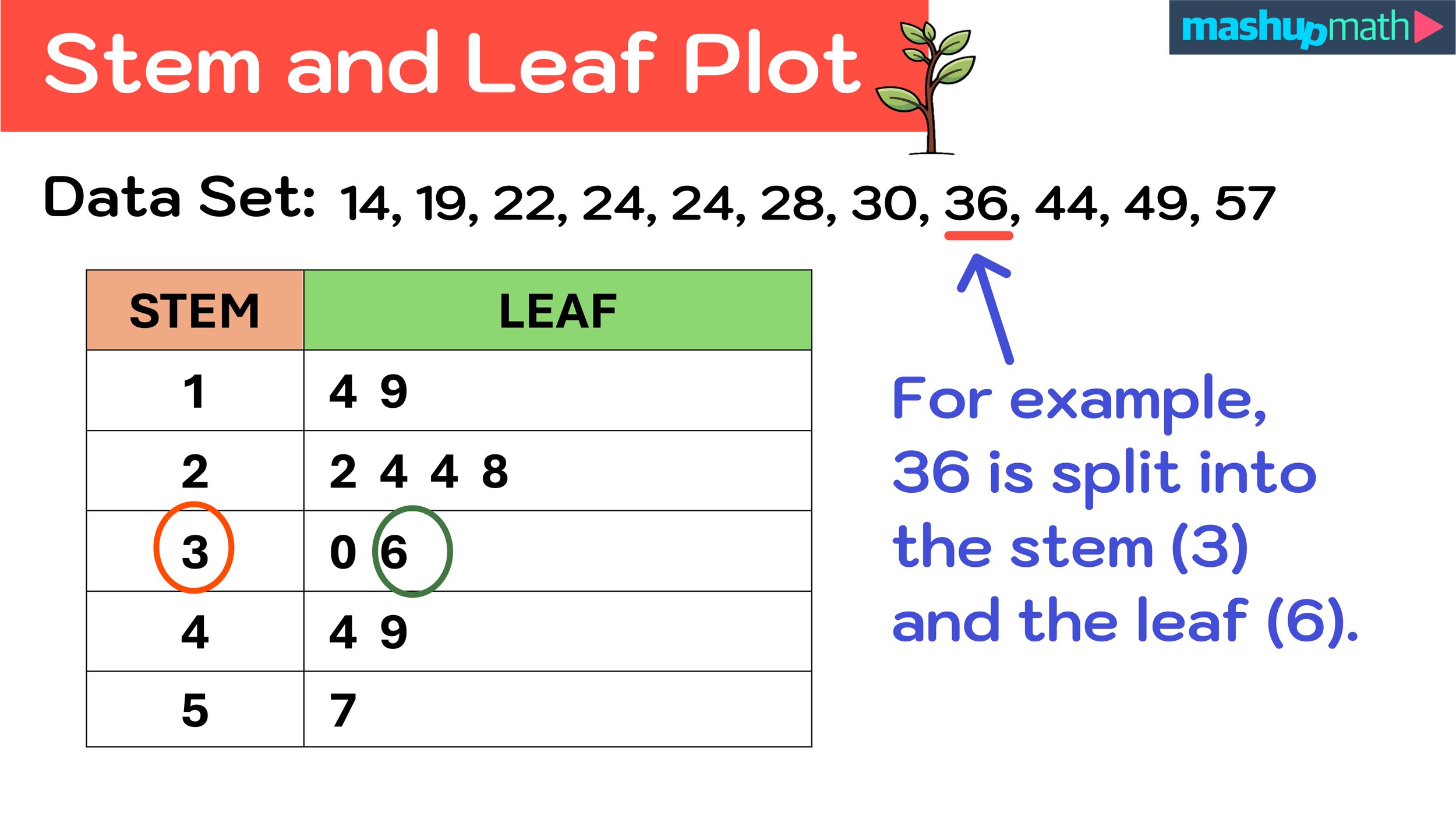
莖葉圖(Stem-and-Leaf Plot)的主要優點是可以同時做到什麼?
答案解析
莖葉圖是一種呈現定量數據分佈的簡單圖形方法,特別適用於小數據集。它將每個數值分成「莖」(通常是較高位數)和「葉」(通常是最低位數)。圖的形狀類似於旋轉
90 度的直方圖,可以展示數據的分佈、集中趨勢和對稱性。與直方圖不同的是,莖葉圖保留了原始數據的數值信息(可以從莖和葉組合還原出原始值或其近似值),而直方圖只顯示了組內的頻數。
#45
★★
列聯表(Contingency Table)或交叉表(Cross-Tabulation)主要用於分析哪種類型數據之間的關係?
答案解析
列聯表是一種以矩陣形式展示兩個(或多個)類別型變數頻率分佈的表格。表格的行代表一個變數的各個類別,列代表另一個變數的各個類別,單元格中的數值則表示同時屬於對應行類別和列類別的觀測數量(頻數)。透過分析列聯表中的頻數、百分比以及進行卡方檢定(Chi-squared
Test)等統計分析,可以判斷這兩個(或多個)類別變數之間是否存在關聯性。

#46
★★
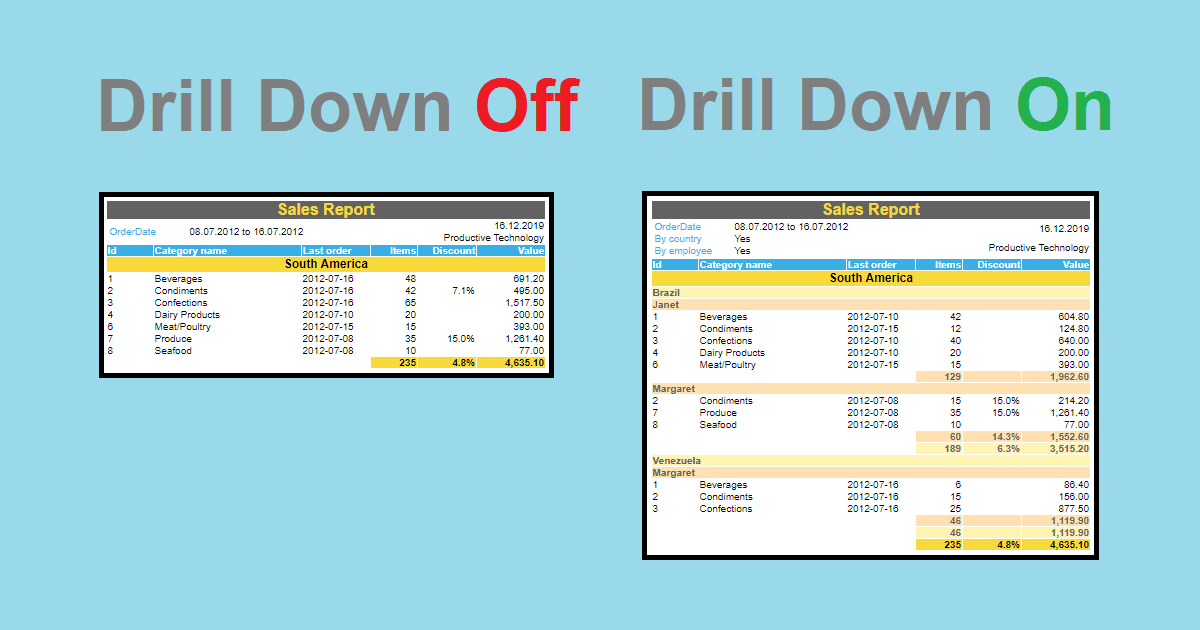
數據儀表板(Dashboard)中常用的「下鑽」(Drill-down)功能指的是?
答案解析
下鑽是互動式儀表板中常見的功能,允許使用者在查看匯總數據時,點擊某個數據點或類別,進一步查看構成該匯總數據的更細粒度的明細數據。例如,在查看全國總銷售額時,可以點擊「北部地區」下鑽查看北部各省份的銷售額,再點擊「某省份」下鑽查看該省各城市的銷售額。這種功能使得使用者可以從宏觀概覽逐步深入到微觀細節,更好地理解數據的層級結構和成因。
#47
★★★
幾何平均數(Geometric Mean)最常用於計算哪一類數據的平均值?
答案解析
幾何平均數是 n 個正數乘積的 n
次方根。它特別適用於計算具有乘法關係或複合效應的數據的平均值,例如:
- 平均增長率:計算多年投資的平均年化報酬率時,應使用幾何平均數,因為每年的報酬率是以前一年的基礎進行複合計算的。
- 平均比率:計算一系列比率數據的平均值。

#48
★
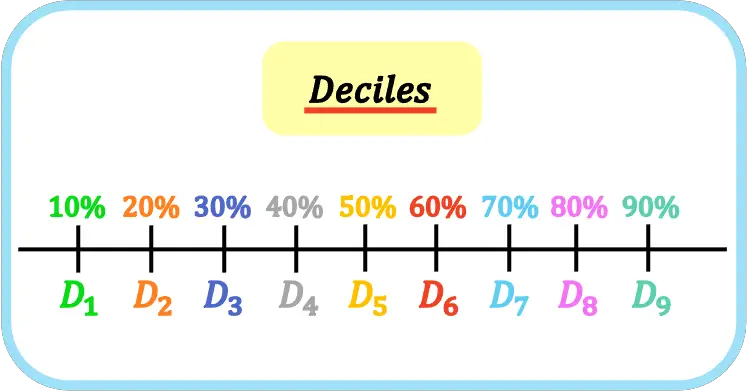
十等分位數(Deciles)將數據分成幾個相等的部分?
答案解析
與四分位數(Quartiles)將數據分成四部分、百分位數(Percentiles)將數據分成一百部分類似,十等分位數(Deciles)是將排序後的數據集分成十個包含相等數量(約 10%)數據點的部分。共有九個十等分位數,分別是 D1, D2, ...,
D9。其中 D1 = P10, D2 = P20, ..., D5 = P50 = Q2 = 中位數,
..., D9 = P90。
#49
★★
累積頻率分佈圖(Cumulative Frequency Distribution Graph 或 Ogive)的 Y 軸通常表示什麼?
答案解析
累積頻率分佈圖(常稱為 Ogive
圖)是用於視覺化數據累積情況的折線圖。其橫軸通常表示數據分組的上限(或有時是組中點),縱軸表示小於或等於該橫軸值的數據點的累積數量(累積頻數)或累積比例(累積相對頻數或累積百分比)。曲線總是呈現非遞減的趨勢,最終達到總頻數或 100%。Ogive 圖可以用來快速估計某個數值對應的百分位數,或某個百分位數對應的數值。
#50
★
在呈現敘述性統計結果時,表格(Table)相比於圖表(Chart)的主要優勢在於?
答案解析
圖表(如長條圖、折線圖、散佈圖)擅長於直觀地展示數據的模式、趨勢、關係和分佈形狀,易於快速理解。然而,它們通常犧牲了數值的精確性。表格則以行列形式組織數據,能夠清晰、準確地呈現大量的詳細數值(例如,具體的平均數、標準差、頻數、百分比到小數點後幾位)。當需要查閱或比較精確數值時,表格是更合適的選擇。通常,一個好的數據報告會結合使用圖表和表格,利用圖表進行視覺化呈現和趨勢說明,利用表格提供精確的數據支持。
沒有找到符合條件的題目。
↑