iPAS AI應用規劃師 考試重點

L22101 敘述性統計與資料摘要技術
主題分類
1
敘述統計基本概念與目的
2
資料類型與整理
3
集中趨勢量數
4
離散趨勢量數
5
資料分佈與形狀
6
資料摘要技術
7
資料視覺化
8
相關性與離群值
#1
★★★★★
敘述統計學 (Descriptive Statistics) - 定義與目的
核心概念
敘述統計學是統計學的一個分支，專注於整理、呈現和總結資料的主要特徵。其主要目的不是進行推論或預測，而是提供對資料集本身的清晰描述。
  • 目的：描述資料的基本情況、找出資料的模式或趨勢、為後續的推論統計分析奠定基礎。
  • 方法：使用圖表（如直方圖、盒鬚圖）和數值（如平均數、標準差）來呈現資料。
#2
★★★★
敘述統計 vs 推論統計
主要區別
  • 敘述統計 (Descriptive Statistics)：描述現有資料的特性（樣本或母體）。
  • 推論統計 (Inferential Statistics)：從樣本資料推斷母體的特性，進行假設檢定、估計或預測。
AI應用規劃師需要理解敘述統計來初步探索和理解數據，這是建立模型的基礎。
#3
★★★★★
資料類型 - 數值型 vs 類別型
基本分類
理解資料類型是選擇合適統計方法和視覺化的前提。
  • 數值型資料 (Numerical Data)：可測量的量化數據。可再分為：
    • 連續型 (Continuous)：可取範圍內任意值（如：身高、溫度）。
    • 離散型 (Discrete)：只能取特定整數值（如：人數、汽車數量）。
  • 類別型資料 (Categorical Data)：描述品質或特性的數據，代表不同的組別或類別。可再分為：
    • 名目型 (Nominal)：類別間無順序（如：顏色、性別）。
    • 次序型 (Ordinal)：類別間有順序關係（如：教育程度、滿意度評級）。
#4
★★★
資料整理 (Data Organization)
常用技術
整理原始資料是進行敘述統計分析的第一步。
  • 頻率分佈表 (Frequency Distribution Table)：顯示各數值或類別出現的次數。
  • 分組 (Grouping)：將連續型資料劃分成不同的區間（組別）。
  • 排序 (Sorting)：將資料依數值大小或類別排序。
#5
★★★★★
集中趨勢量數 - 平均數 (Mean)
定義與特性
平均數是最常用的集中趨勢量數，代表資料的算術平均值。
  • 計算：所有數值總和除以數值個數。
  • 優點：計算簡單，納入所有資料點的資訊。
  • 缺點：容易受到極端值（離群值）的影響。
  • 適用：主要用於對稱分佈的數值型資料。
#6
★★★★★
集中趨勢量數 - 中位數 (Median)
定義與特性
中位數是將資料排序後位於中間位置的數值。
  • 計算：奇數個數時取中間值；偶數個數時取中間兩個數的平均值。
  • 優點：不受極端值的影響，適用於偏態分佈。
  • 缺點：計算相對複雜（需排序），未利用所有數據的數值大小。
  • 適用：偏態分佈的數值型資料、次序型資料。
#7
★★★★
集中趨勢量數 - 眾數 (Mode)
定義與特性
眾數是資料集中出現次數最多的數值或類別。
  • 特性：可能沒有眾數，也可能有多個眾數（單峰、雙峰、多峰）。
  • 優點：適用於所有資料類型（數值型、類別型），不受極端值影響，易於理解。
  • 缺點：不穩定，可能不存在或不唯一，未考慮數據的數值大小。
  • 適用：類別型資料（尤其是名目型），或想找出最常見數值時。
#8
★★★
選擇集中趨勢量數的考量
適用情境
選擇哪種量數取決於資料類型和分佈形狀：
  • 對稱分佈：平均數、中位數、眾數通常很接近，平均數最常用。
  • 偏態分佈：中位數通常是比平均數更好的代表。
  • 類別型資料：通常使用眾數。
  • 有極端值：中位數比平均數更穩健。
#9
★★★★
離散趨勢量數 - 全距 (Range)
定義與特性
全距是衡量資料分散程度的最簡單方法。
  • 計算：最大值減去最小值。
  • 優點：計算非常簡單。
  • 缺點：只考慮最大和最小值，極易受極端值影響，無法反映資料內部的分散情況。
#10
★★★★★
離散趨勢量數 - 變異數 (Variance)
定義與特性
變異數衡量資料點相對於平均數的分散程度的平均值。
  • 計算：每個資料點與平均數差值的平方和，再除以資料點總數（母體變異數 σ²）或總數減一（樣本變異數 s²）。
  • 特性：單位是原始資料單位的平方，不易直觀解釋。值越大，表示資料越分散。
  • 使用樣本變異數 (n-1) 的原因：對母體變異數的不偏估計。
#11
★★★★★
離散趨勢量數 - 標準差 (Standard Deviation)
定義與特性
標準差是變異數的平方根，是最常用的離散趨勢量數。
  • 計算：√變異數 (母體: σ, 樣本: s)。
  • 優點：單位與原始資料相同，易於解釋。衡量資料點偏離平均數的典型距離。
  • 特性：值越大，表示資料越分散。對於常態分佈，有經驗法則（68-95-99.7法則）。
  • 缺點：同樣會受到極端值的影響。
#12
★★★★
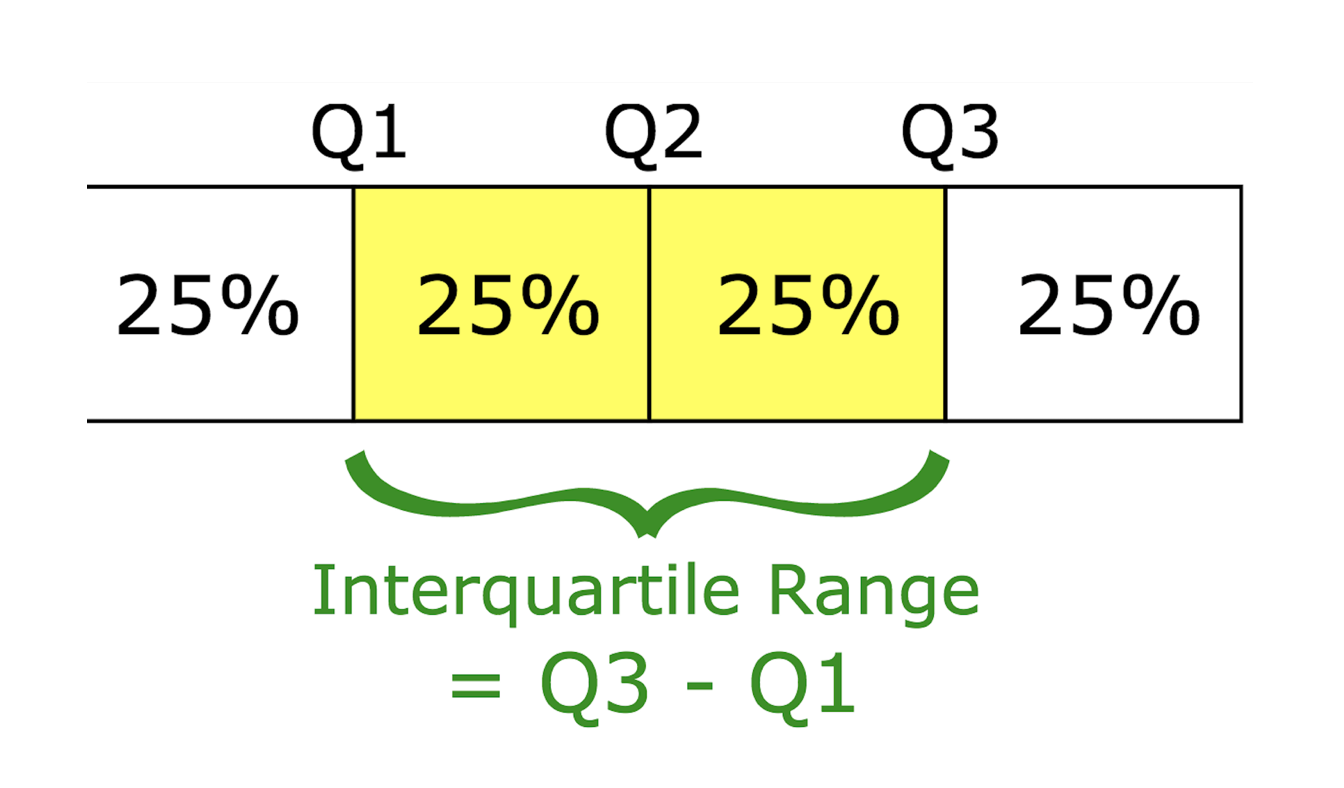
離散趨勢量數 - 四分位距 (Interquartile Range, IQR)
定義與特性
四分位距描述資料中間50%範圍的分散程度。
  • 計算：第三四分位數 (Q3) 減去 第一四分位數 (Q1)。(IQR = Q3 - Q1)
  • 四分位數 (Quartiles)：將排序後的資料分成四等份的數值點 (Q1: 25%, Q2: 50% (即中位數), Q3: 75%)。
  • 優點：不受極端值的影響，適用於偏態分佈。常用於盒鬚圖和離群值檢測。
#13
★★★
變異係數 (Coefficient of Variation, CV)
定義與目的
變異係數是標準差與平均數的比值，用來比較不同單位或不同平均數的資料集之間的相對離散程度。
  • 計算：(標準差 / 平均數) * 100%。
  • 特性：無單位，是一個相對值。
  • 適用：比較公斤和公分資料的離散程度，或比較平均銷售額差異很大的兩組產品的銷售額穩定性。
#14
★★★★
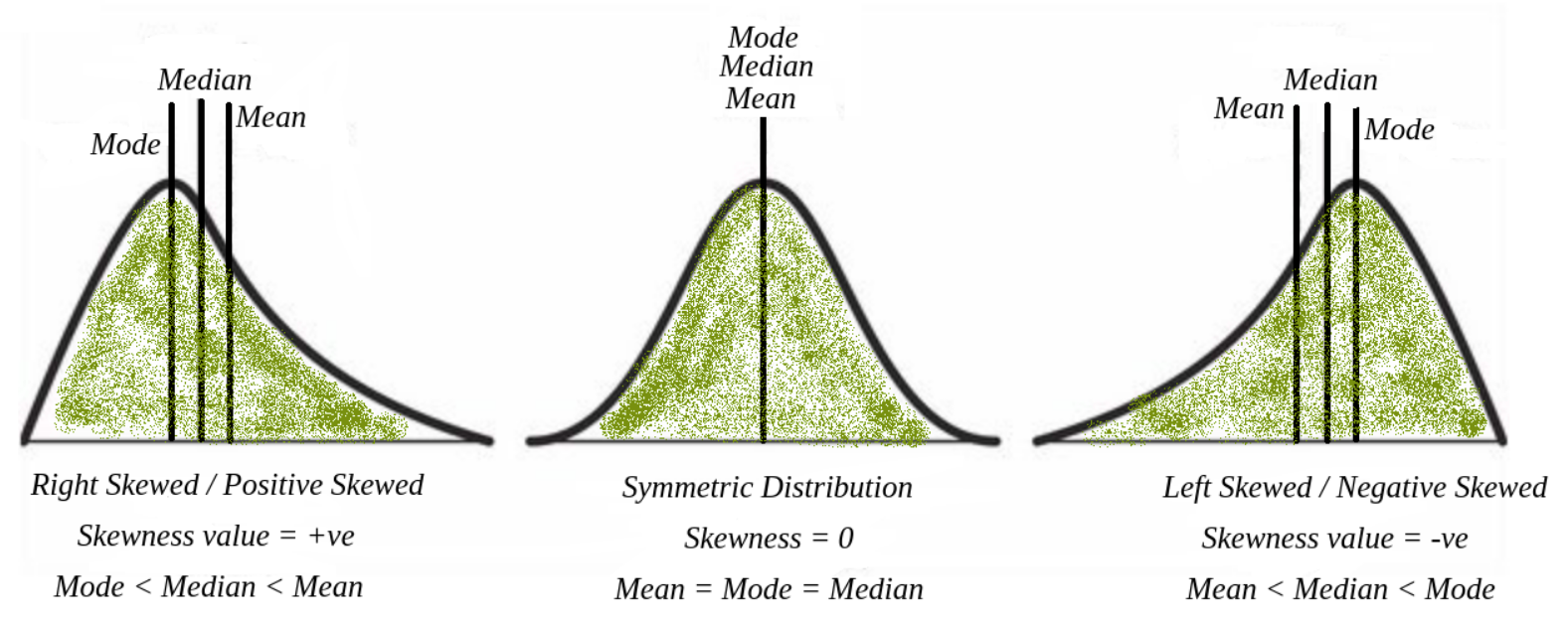
資料分佈形狀 - 偏態 (Skewness)
定義與判斷
偏態描述資料分佈的不對稱性。
  • 右偏態 (Right-skewed / Positive Skewness)：尾巴向右延伸，眾數 < 中位數 < 平均數。
  • 左偏態 (Left-skewed / Negative Skewness)：尾巴向左延伸，平均數 < 中位數 < 眾數。
  • 對稱分佈 (Symmetric Distribution)：左右對稱，平均數 ≈ 中位數 ≈ 眾數。
偏態影響集中趨勢量數的選擇（偏態時用中位數較佳）。
#15
★★★
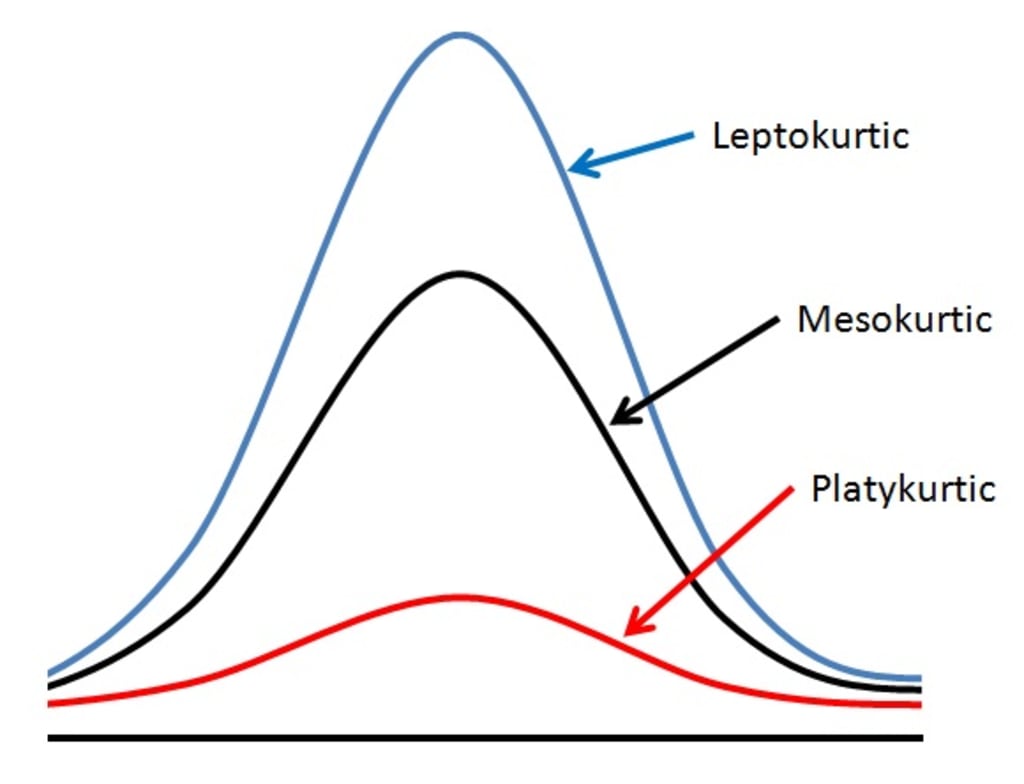
資料分佈形狀 - 峰度 (Kurtosis)
定義與類型
峰度描述資料分佈峰部的尖銳程度以及尾部的厚重程度（相對於常態分佈）。
  • 高狹峰 (Leptokurtic)：比常態分佈更尖峭，尾部更厚重（峰度 > 3 或 超額峰度 > 0）。表示離群值較多。
  • 低闊峰 (Platykurtic)：比常態分佈更平坦，尾部更輕薄（峰度 < 3 或 超額峰度 < 0）。表示離群值較少。
  • 常態峰 (Mesokurtic)：峰度接近常態分佈（峰度 ≈ 3 或 超額峰度 ≈ 0）。
超額峰度 (Excess Kurtosis) = 峰度 - 3。
#16
★★★★
資料摘要技術 - 頻率分佈 (Frequency Distribution)
應用
用於總結類別型資料或分組後的數值型資料中各個值或組別出現的次數。
  • 絕對頻率：實際出現的次數。
  • 相對頻率：次數佔總數的比例或百分比。
  • 累積頻率：小於等於某個值或組別上限的次數累加。
是製作長條圖、圓餅圖、直方圖的基礎。
#17
★★★
資料摘要技術 - 百分位數 (Percentiles)
定義與應用
百分位數（如P90, P50, P25）表示資料集中有多少百分比的數值小於該數值。
  • 例如，第90百分位數（P90）表示90%的資料小於此值。
  • 第50百分位數（P50）即為中位數。
  • 第25百分位數（P25）為第一四分位數（Q1），第75百分位數（P75）為第三四分位數（Q3）。
常用於描述資料點在整體中的相對位置（如考試成績排名）。
#18
★★★★
資料摘要技術 - 列聯表 (Contingency Table / Cross-Tabulation)
應用
用於總結兩個或多個類別型變數之間的關係。表格顯示了變數組合的頻率。
  • 例如，分析不同性別（變數1）購買不同產品類別（變數2）的人數。
  • 可以計算聯合頻率、邊際頻率和條件頻率。
是進行卡方檢定等分析的基礎。
#19
★★★★★
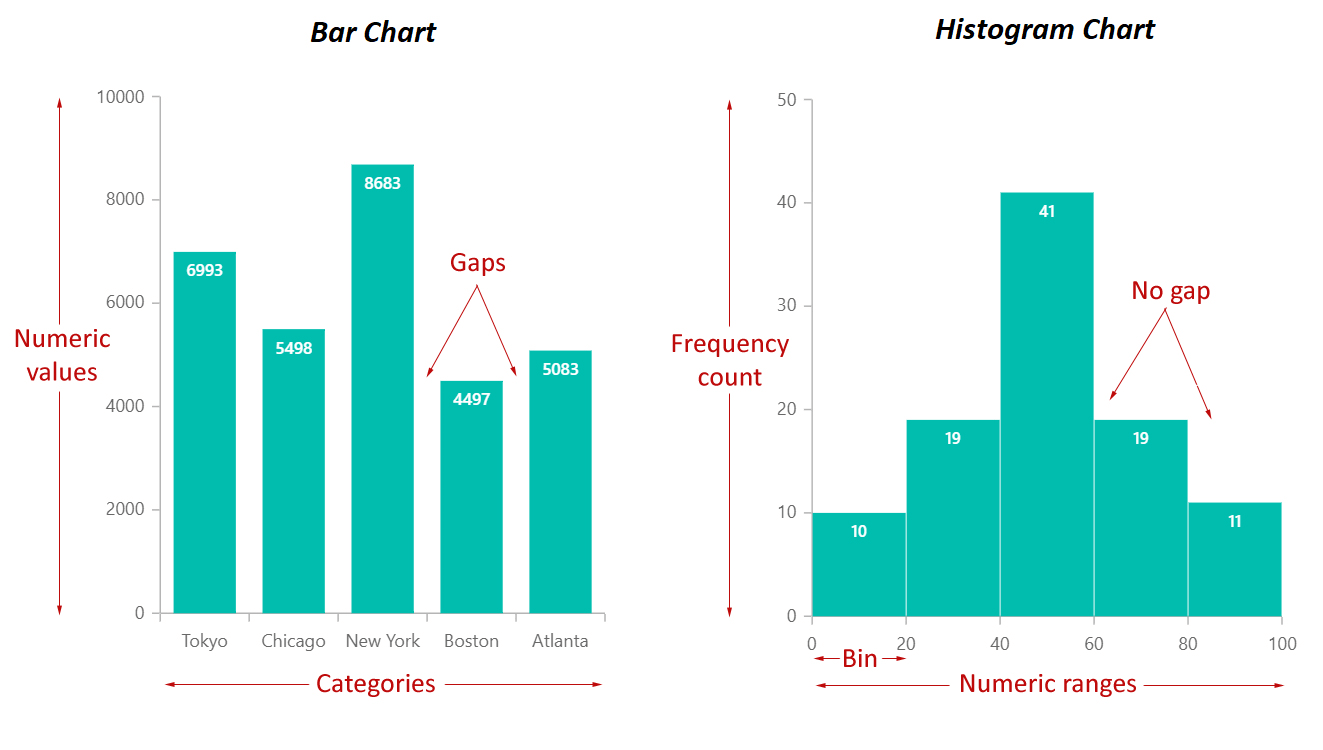
資料視覺化 - 長條圖 (Bar Chart)
適用情境與判讀
  • 用途：比較不同類別型資料的頻率或數值大小。
  • 構成：X軸代表類別，Y軸代表頻率或數值，使用分離的長條表示。
  • 判讀：比較長條的高度來判斷各類別的相對大小。
  • 注意：與直方圖不同，長條圖的長條之間有間隔。
#20
★★★★
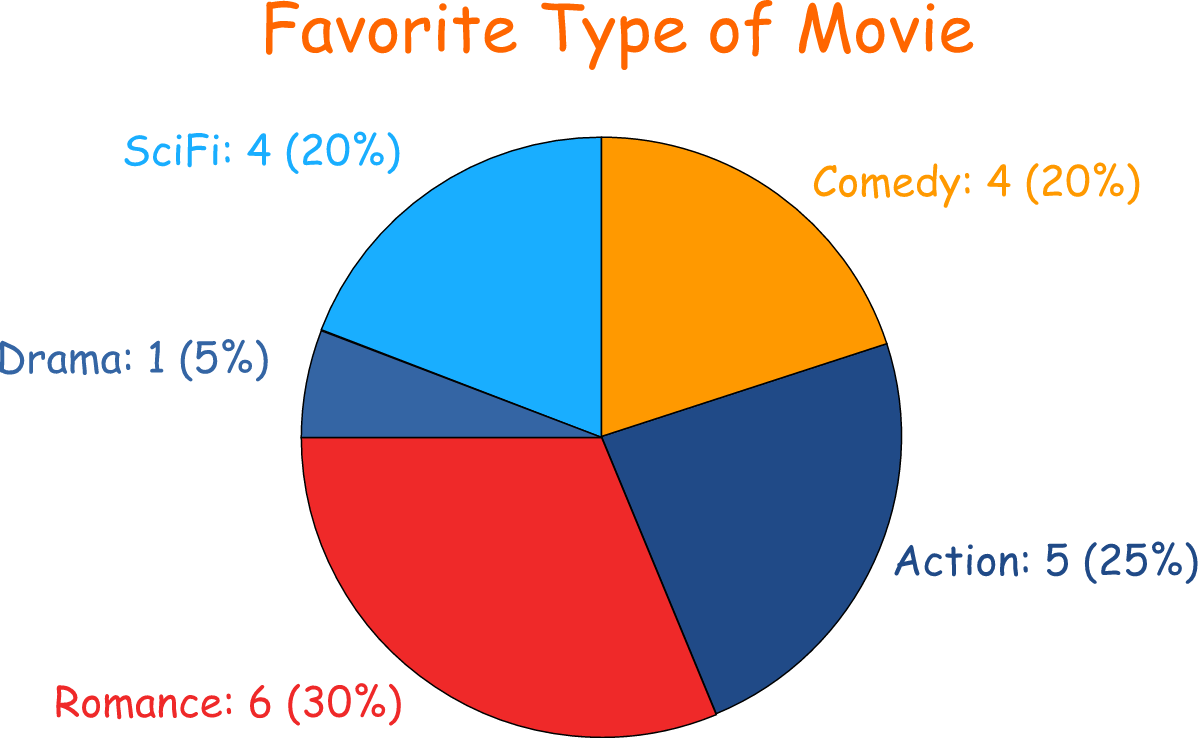
資料視覺化 - 圓餅圖 (Pie Chart)
適用情境與判讀
  • 用途：顯示類別型資料各部分佔整體的比例或百分比。
  • 構成：整個圓代表總體 (100%)，扇形面積大小代表各類別的比例。
  • 判讀：比較扇形面積來了解各部分的相對重要性。
  • 缺點：當類別過多或比例接近時，不易精確比較，長條圖通常是更好的選擇。
#21
★★★★★
資料視覺化 - 直方圖 (Histogram)
適用情境與判讀
  • 用途：顯示數值型資料（通常是連續型）的頻率分佈。
  • 構成：X軸代表數值區間（組距），Y軸代表該區間內的頻率，使用相鄰的長條表示。
  • 判讀：觀察圖形的整體形狀（對稱、偏態）、中心位置和分散程度。
  • 注意：長條之間沒有間隔（除非某區間頻率為0）。選擇合適的組距很重要。
#22
★★★★★
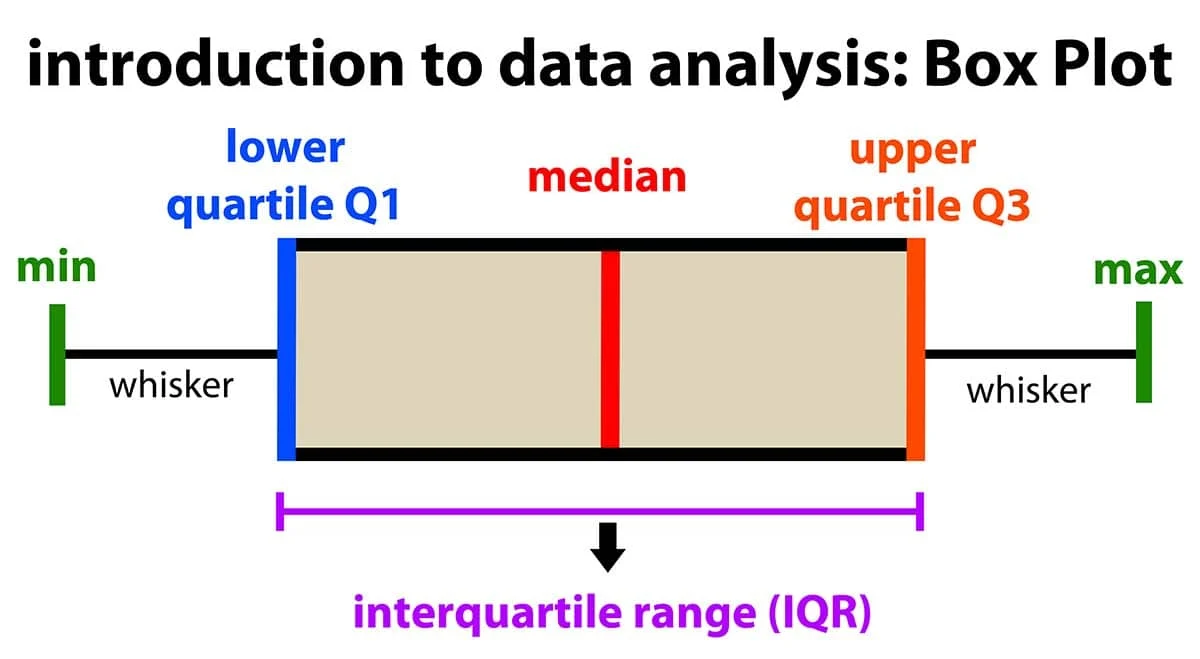
資料視覺化 - 盒鬚圖 (Box Plot / Box-and-Whisker Plot)
適用情境與判讀
  • 用途：顯示數值型資料的五數摘要（最小值、Q1、中位數(Q2)、Q3、最大值），並可用於比較不同組別的分佈。
  • 構成：
    • 盒子：包含中間50%的資料（從Q1到Q3），盒內的線代表中位數(Q2)。
    • 盒鬚 (Whiskers)：從盒子延伸出去，通常代表資料的主要範圍（如延伸到距離Q1/Q3 1.5倍IQR內的點）。
    • 離群值 (Outliers)：超出盒鬚範圍的點，通常單獨標示。
  • 判讀：觀察中位數位置、盒子長度（IQR，分散程度）、盒鬚長度、對稱性以及是否有離群值。
#23
★★★★
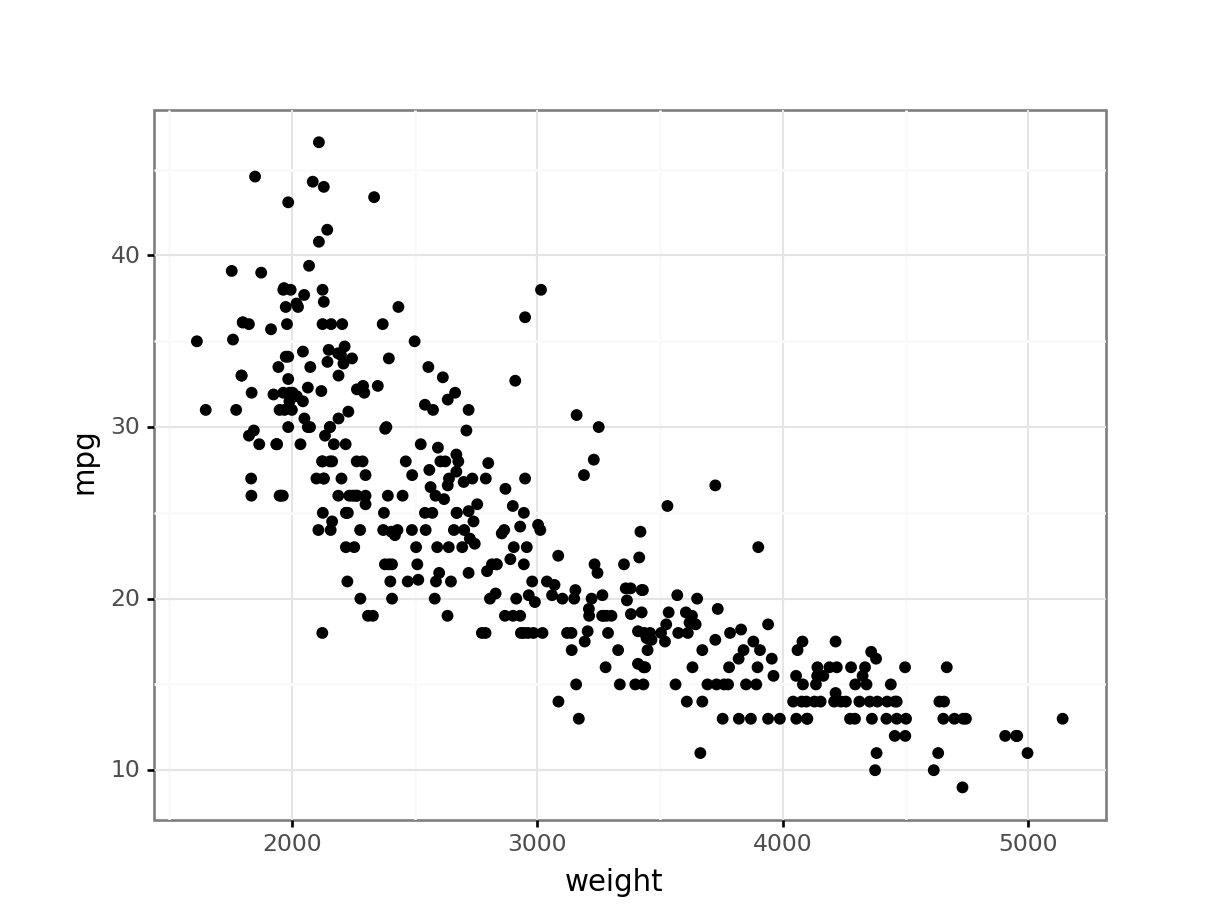
資料視覺化 - 散佈圖 (Scatter Plot)
適用情境與判讀
  • 用途：顯示兩個數值型變數之間的關係。
  • 構成：每個資料點對應一對(X, Y)值，繪製在二維座標系上。
  • 判讀：觀察點的分佈模式，判斷變數間是否存在正相關、負相關、無相關或非線性關係，以及關係的強度。
#24
★★★★
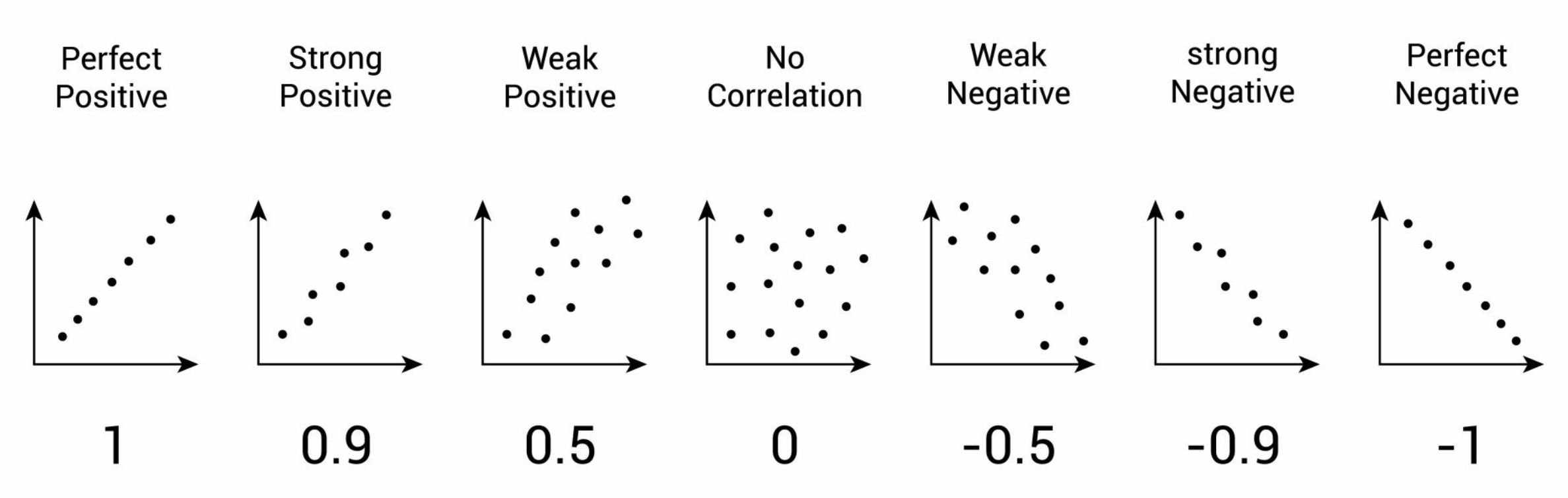
相關係數 (Correlation Coefficient) - 皮爾森相關係數 (Pearson r)
定義與判讀
  • 用途：量化兩個數值型變數之間線性關係的強度和方向。
  • 範圍：介於 -1 到 +1 之間。
    • +1：完全正相關。
    • -1：完全負相關。
    • 0：無線性相關。
  • 強度：絕對值越接近1，線性關係越強。
  • 注意：相關不等於因果關係。僅衡量線性關係，無法反映非線性關係。
#25
★★★★
離群值 (Outliers) - 偵測方法
常用技術
離群值是指顯著偏離資料集中其他觀測值的數值。
  • 視覺化方法：盒鬚圖 (Box Plot) 是最常用的方法，超出盒鬚的點被視為離群值。散佈圖也可觀察。
  • IQR 法則：常用的離群值判斷標準是小於 Q1 - 1.5 * IQR 或大於 Q3 + 1.5 * IQR 的值。
  • 標準差法 (Z-score)：將資料標準化後（計算Z分數），通常認為 Z 分數絕對值大於 2 或 3 的值為離群值。此法假設資料接近常態分佈。
#26
★★★
離群值 (Outliers) - 處理方式
應對策略
處理離群值需謹慎，應先了解其成因。
  • 識別與驗證：確認是否為輸入錯誤或測量誤差。若是，則予以修正或刪除。
  • 保留：若離群值是真實且重要的觀測值（如欺詐檢測中的異常交易），則應保留。
  • 轉換：對資料進行數學轉換（如對數轉換），可能減輕離群值的影響。
  • 設限 (Capping/Winsorizing)：將離群值替換為某個預設的最大值或最小值（如第99百分位數）。
  • 刪除：若確定為錯誤且無法修正，或對模型有極大負面影響，可考慮刪除，但需記錄原因和影響。
#27
★★★
母體 (Population) vs 樣本 (Sample)
基本定義
  • 母體：研究感興趣的所有個體的集合。
  • 樣本：從母體中抽取的一部分個體的集合。
敘述統計可以用來描述樣本資料，也可以用來描述整個母體資料（如果可得）。推論統計則是用樣本來推論母體。
#28
★★
時間序列資料 (Time Series Data)
特性
時間序列資料是按時間順序收集的觀測值（如每日股價、每月銷售額）。雖然有特定的分析方法（如移動平均），但基本的敘述統計（如計算趨勢線、描述季節性波動）也適用於初步探索。
#29
★★★
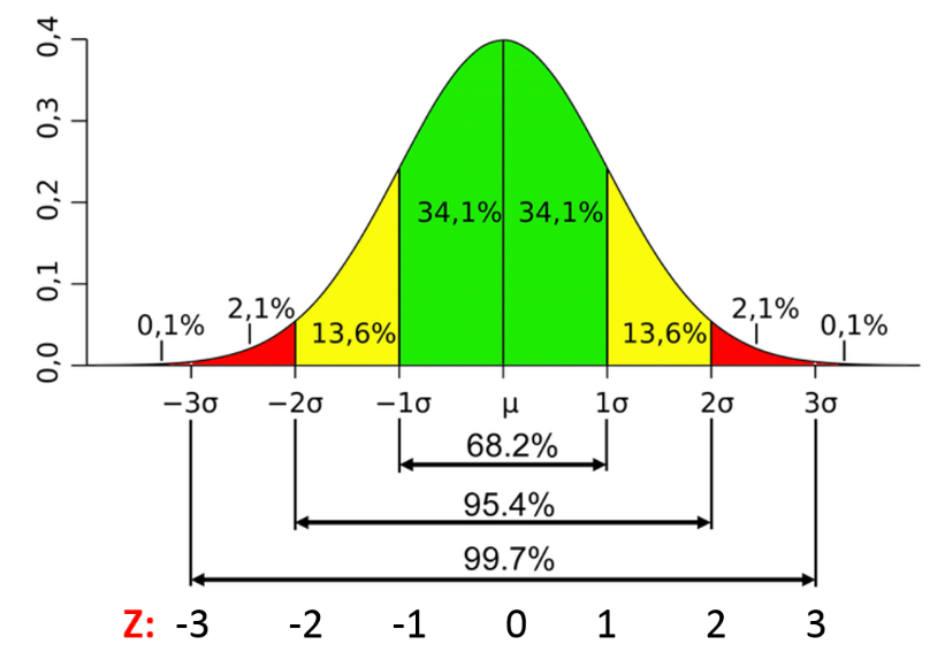
常態分佈 (Normal Distribution) 特性
關鍵特徵
常態分佈（又稱高斯分佈）是一種常見的連續機率分佈。
  • 形狀：鐘形 (Bell-shaped)、單峰 (Unimodal)、左右對稱 (Symmetric)。
  • 集中趨勢：平均數 = 中位數 = 眾數。
  • 經驗法則 (68-95-99.7 Rule)：約68%的資料落在平均數±1個標準差內；約95%落在±2個標準差內；約99.7%落在±3個標準差內。
許多統計推論方法假設資料來自常態分佈。
#30
★★★
資料視覺化 - 線圖 (Line Chart)
適用情境
  • 用途：顯示資料（通常是數值型）隨時間變化的趨勢。
  • 構成：X軸通常代表時間，Y軸代表數值，用線連接各時間點的數值。
  • 判讀：觀察線的上升、下降、波動等趨勢。
#31
★★
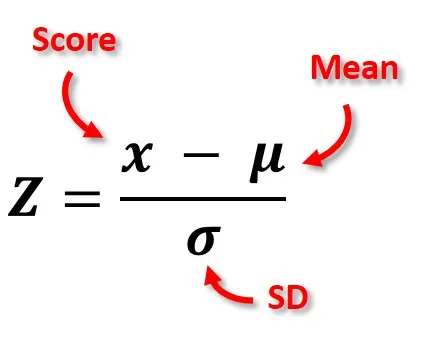
標準分數 (Standard Score / Z-score)
定義與用途
Z分數表示一個數值距離平均數有多少個標準差。
  • 計算：Z = (觀測值 - 平均數) / 標準差。
  • 用途：
    • 比較不同單位或不同分佈的數值。
    • 偵測離群值（如 |Z| > 3）。
    • 資料標準化，用於某些機器學習演算法。
  • 特性：標準化後的資料平均數為0，標準差為1。
#32
★★★
視覺化選擇原則
考量因素
選擇合適的圖表需考慮：
  • 分析目的：是比較、看分佈、看關係、還是看組成？
  • 資料類型：是數值型還是類別型？是一個變數還是多個變數？
  • 受眾：圖表是否清晰易懂？
  • 避免誤導：例如，Y軸不從0開始可能誇大差異。
#33
★★
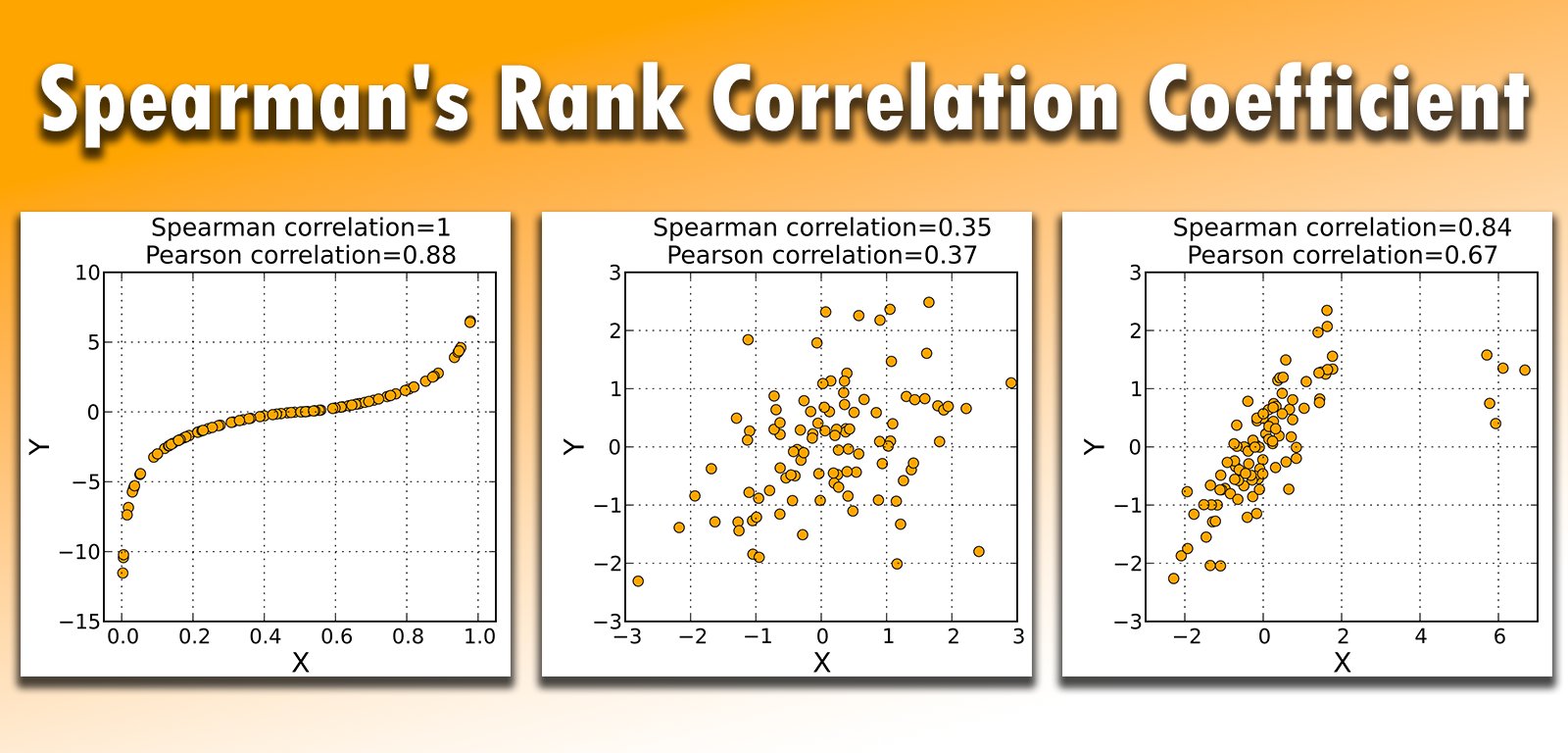
斯皮爾曼等級相關係數 (Spearman Rank Correlation)
定義與用途
斯皮爾曼相關是非參數的相關性度量，評估兩個變數等級之間單調關係的強度。
  • 計算：基於變數的排序（等級）而非原始數值。
  • 用途：
    • 當變數是次序型資料時。
    • 當數值型變數的關係是非線性但單調（即一個變數增加時，另一個變數也傾向於增加或減少，但不一定是直線）時。
    • 對離群值較不敏感。
  • 範圍與解釋：同皮爾森相關係數 (-1 到 +1)。
#34
★★
幾何平均數 (Geometric Mean)
定義與用途
幾何平均數用於計算一組數值的中心趨勢，特別適用於比率或百分比變化率的平均。
  • 計算：n個數值乘積的n次方根。
  • 用途：計算平均年增長率、投資報酬率等。
  • 特性：受極小值影響大，若有0則結果為0。數值必須為正。
#35
★
平均絕對離差 (Mean Absolute Deviation, MAD)
定義
MAD是另一種衡量資料分散程度的方法，計算每個資料點與平均數差值的絕對值的平均。
  • 相較於標準差，它對離群值的敏感度較低（因為沒有平方）。
  • 但數學性質不如標準差好，較少用於推論統計。
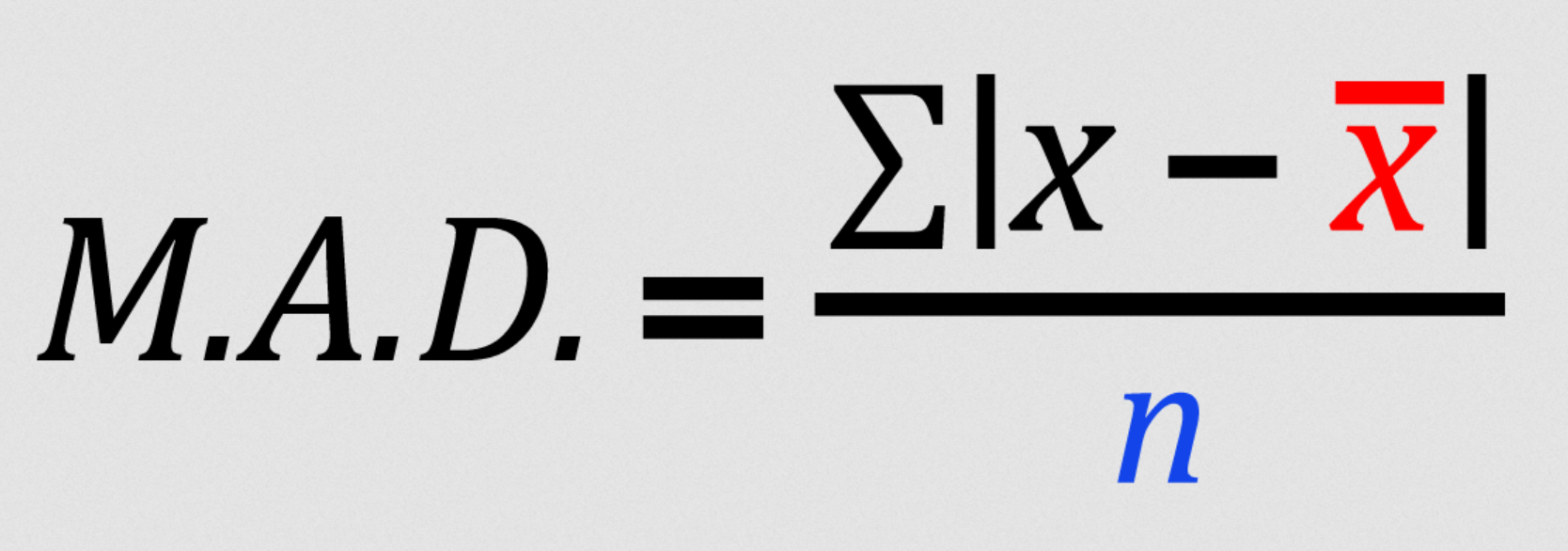
#36
★★
熱力圖 (Heatmap)
視覺化目的
熱力圖使用顏色強度來表示矩陣中數值的大小。
  • 用途：常應用於視覺化相關係數矩陣、列聯表中的數值、或地理空間資料的密度。
  • 可以快速識別矩陣中的高值和低值區域以及模式。
#37
★★★
敘述統計在AI專案中的角色
重要性
在建立AI模型前，敘述統計是探索性資料分析(Exploratory Data Analysis, EDA) 的關鍵環節。
  • 理解資料：了解變數的分佈、中心點、離散程度。
  • 資料清理：識別錯誤值、缺失值、離群值。
  • 特徵工程：提供選擇或轉換特徵的依據。
  • 溝通發現：用圖表和摘要統計向利害關係人展示資料洞見。
#38
★★
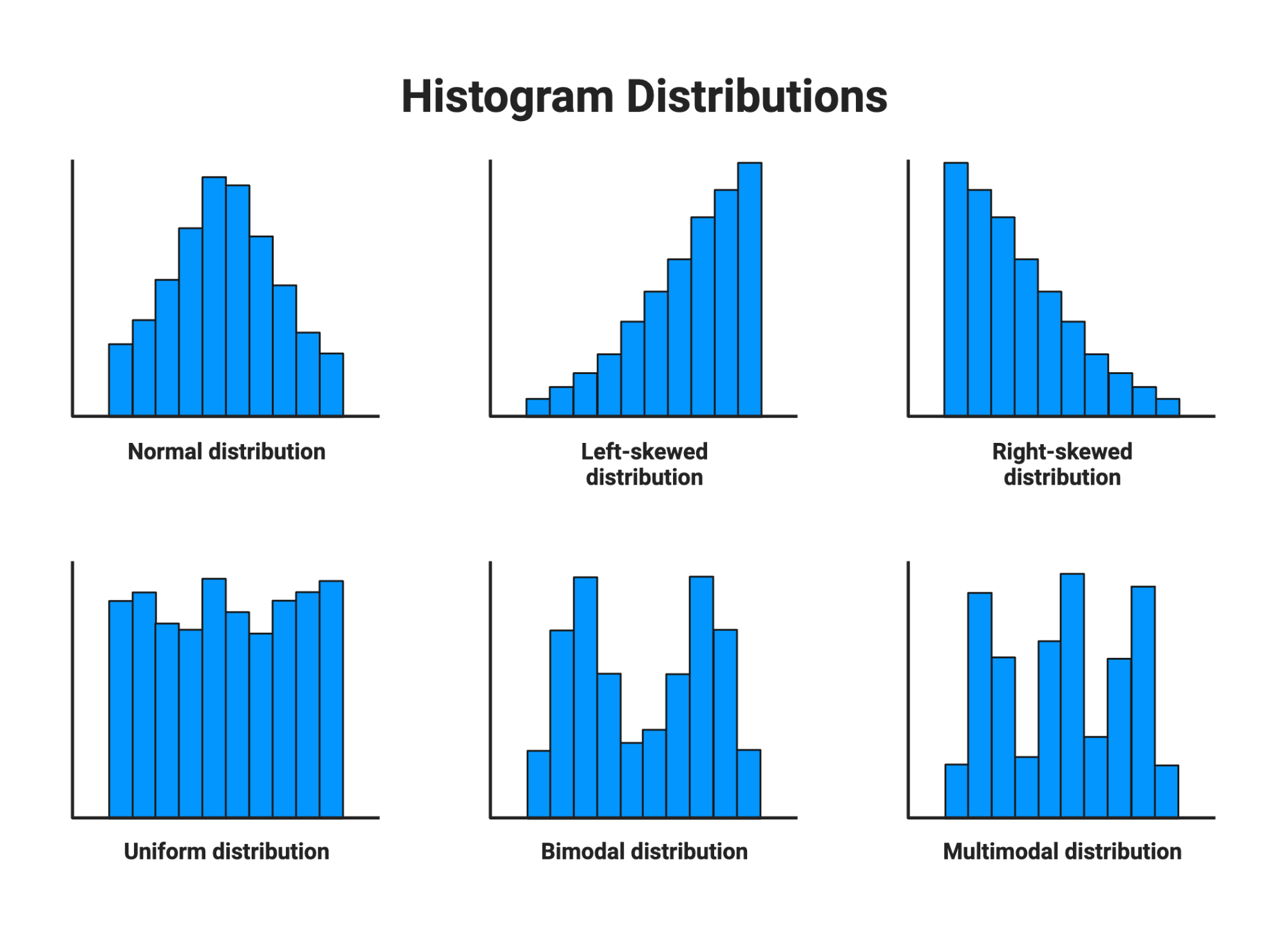
雙峰分佈 (Bimodal Distribution)
特性與意義
雙峰分佈是指資料分佈中出現兩個明顯的峰值（兩個眾數）。
  • 這通常暗示資料可能來自兩個不同的潛在群體或過程。
  • 例如，混合了男性和女性身高的資料集可能呈現雙峰。
  • 遇到雙峰分佈時，單一的集中趨勢量數（如平均數）可能不具代表性，可能需要分開分析兩個群體。
沒有找到符合條件的重點。
↑