iPAS AI應用規劃師 經典題庫

L21301 數據準備與模型選擇
出題方向
1
數據收集與理解
2
數據清洗
3
數據預處理
4
特徵工程
5
數據集劃分與驗證
6
模型選擇基礎 (偏差/變異/擬合)
7
常見模型比較與選擇
8
模型評估指標
#1
★★★★
在進行數據分析專案時，下列哪個步驟通常最先進行？
A
定義問題與收集相關數據
B
訓練機器學習模型
C
評估模型效能
D
部署模型上線
答案解析
任何數據分析或機器學習專案的首要步驟是清晰地定義要解決的問題、目標是什麼，然後根據問題定義去收集相關的數據。沒有明確的問題定義和相關數據，後續的數據處理、模型訓練和評估都無法有效進行。數據收集與理解是整個流程的基礎。
#2
★★★★★
面對數據中的缺失值（Missing Values），以下哪種處理方式最不恰當？
A
直接刪除包含缺失值的整筆記錄（列）
B
使用該欄位的平均數（Mean）或中位數（Median）進行填補
C
使用該欄位的眾數（Mode）進行填補（適用於類別特徵）
D
直接將缺失值當作一個特殊的類別或數值（例如填補 -999）而不告知模型
答案解析
A、B、C 都是常見處理缺失值的方法，各有適用場景和優缺點。刪除記錄（A）簡單但可能損失大量資訊，特別是當缺失值比例高或缺失模式非隨機時。用平均數/中位數（B）或眾數（C）填補能保留樣本，但可能扭曲數據分佈或引入偏差。選項 D 的做法，雖然有時會將缺失本身視為一種資訊（例如建立一個 "IsMissing" 的特徵），但若直接用一個特殊數值（如-999）填補數值型特徵，且模型不知道這個值的特殊含義，模型可能會錯誤地將其當作一個極端但有效的數值來處理，嚴重影響模型效能，因此通常是不恰當的，除非模型本身能處理或有特殊標記告知。
#3
★★★★★
對於數值型特徵進行「標準化」（Standardization）的主要目的是？
A
將所有數值轉換到 [0, 1] 的區間內
B
將特徵數值轉換為平均數為 0，標準差為 1 的分佈，使不同尺度的特徵具有可比性
C
將數值型特徵轉換為類別型特徵
D
處理數據中的離群值（Outliers）
答案解析
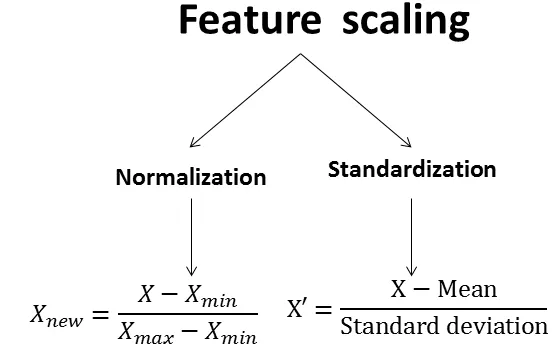
標準化（通常指 Z-score standardization）是常用的數據預處理步驟，計算公式為 (X - μ) / σ，其中 μ 是特徵的平均數，σ 是標準差。標準化的主要目的是消除不同特徵之間因尺度（單位或數值範圍）不同而帶來的影響。許多機器學習演算法（如基於距離的演算法 SVM、KNN，或需要梯度下降優化的模型如線性回歸、神經網路）對特徵的尺度敏感，標準化可以使不同特徵具有相似的尺度和重要性，有助於模型更快收斂且表現更好。選項A描述的是「最小最大縮放」（Min-Max Scaling）或稱為正規化（Normalization）。
#4
★★★★★
處理具有多個類別（例如：紅、黃、藍）的類別型特徵時，以下哪種編碼方式最常用且能避免引入序數關係？
A
標籤編碼（Label Encoding）
B
獨熱編碼（One-Hot Encoding）
C
二進制編碼（Binary Encoding）
D
頻率編碼（Frequency Encoding）
答案解析
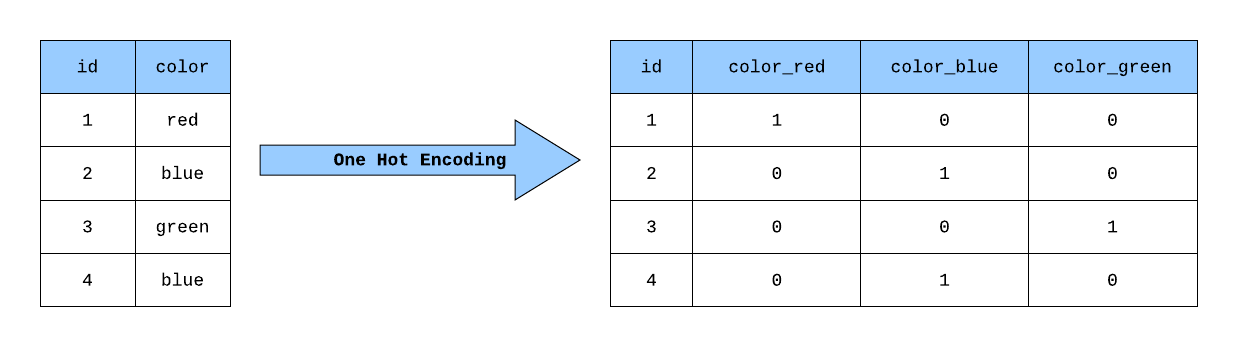
標籤編碼（Label Encoding）會將類別（紅、黃、藍）直接映射為數值（如 0, 1, 2）。對於沒有內在順序關係的名目變數（Nominal Variable），這會錯誤地引入序數關係（例如模型可能認為 2 > 1 > 0），影響模型學習。獨熱編碼（One-Hot Encoding）則為每個類別創建一個新的二元（0 或 1）特徵欄位，如果樣本屬於某個類別，則對應欄位為 1，其餘為 0（例如：紅 -> [1, 0, 0], 黃 -> [0, 1, 0], 藍 -> [0, 0, 1]）。這種方式消除了序數關係，讓每個類別平等，是處理名目變數最常用的方法，但缺點是當類別數量很多時會導致維度大幅增加。
#5
★★★★
特徵工程（Feature Engineering）在機器學習流程中的主要目標是？
A
增加數據集的樣本數量
B
選擇最複雜的機器學習模型
C
從原始數據中創建、選擇或轉換出更能有效表徵問題、提升模型效能的特徵
D
直接將原始數據輸入模型進行訓練
答案解析
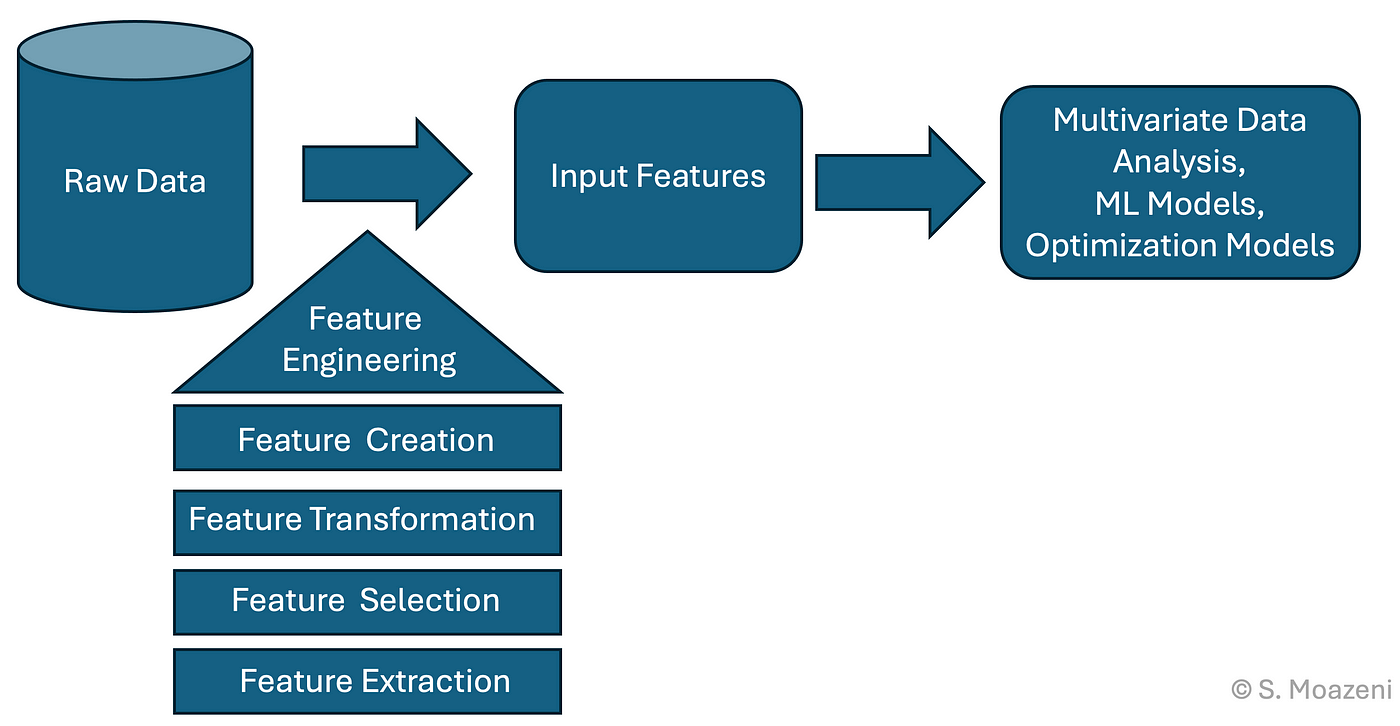
特徵工程是利用領域知識和數據分析技巧，對原始數據進行加工處理，以提取或構建出對預測目標更有幫助的特徵變數的過程。好的特徵能夠更清晰地反映數據中的模式和關係，使得相對簡單的模型也能達到良好的效果。它包括特徵創建（如從日期中提取星期幾、從地址中提取區域）、特徵選擇（移除冗餘或不相關特徵）、特徵轉換（如對數轉換、多項式特徵）、特徵提取（如PCA降維）等步驟。特徵工程的品質往往對最終模型效能有決定性影響。
#6
★★★★★
在機器學習中，將數據集劃分為訓練集（Training Set）、 驗證集（Validation Set）和 測試集（Test Set）的主要目的是？
A
加快模型訓練速度
B
訓練模型、調整模型超參數、評估模型最終泛化能力
C
增加數據的多樣性
D
減少所需的數據量
答案解析
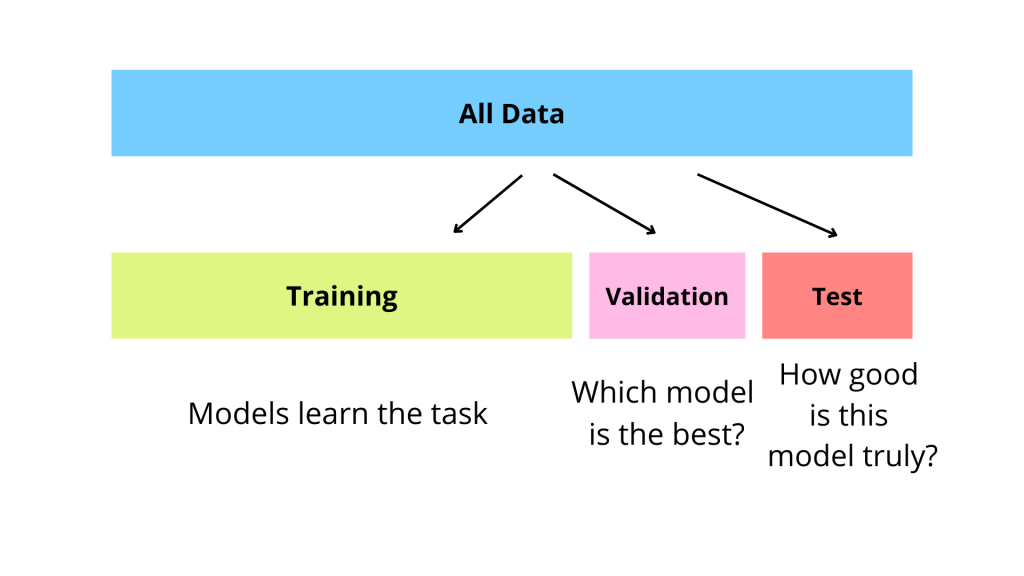
這種劃分是為了可靠地評估和選擇模型。
  • 訓練集（Training Set）：用於訓練模型，調整模型的內部參數（權重）。
  • 驗證集（Validation Set）：用於在訓練過程中監控模型效能，並用來調整模型的超參數（Hyperparameters，如學習率、樹的深度、正規化強度等），或者進行模型選擇（比較不同模型的效能）。
  • 測試集（Test Set）：在模型訓練和超參數調整完成後，用於評估最終選定模型的泛化能力（在從未見過的數據上的表現）。測試集的效能是模型最終效能的無偏估計，它不應參與任何訓練或調參過程，以避免資訊洩漏。
#7
★★★★
K-摺交叉驗證（K-Fold Cross-Validation）是一種常用的模型驗證技術，其主要優點是？
A
訓練速度非常快
B
更充分地利用數據，得到更穩健的模型效能評估，減少因單次劃分帶來的偶然性
C
完全不需要測試集
D
可以自動選擇最佳特徵
答案解析
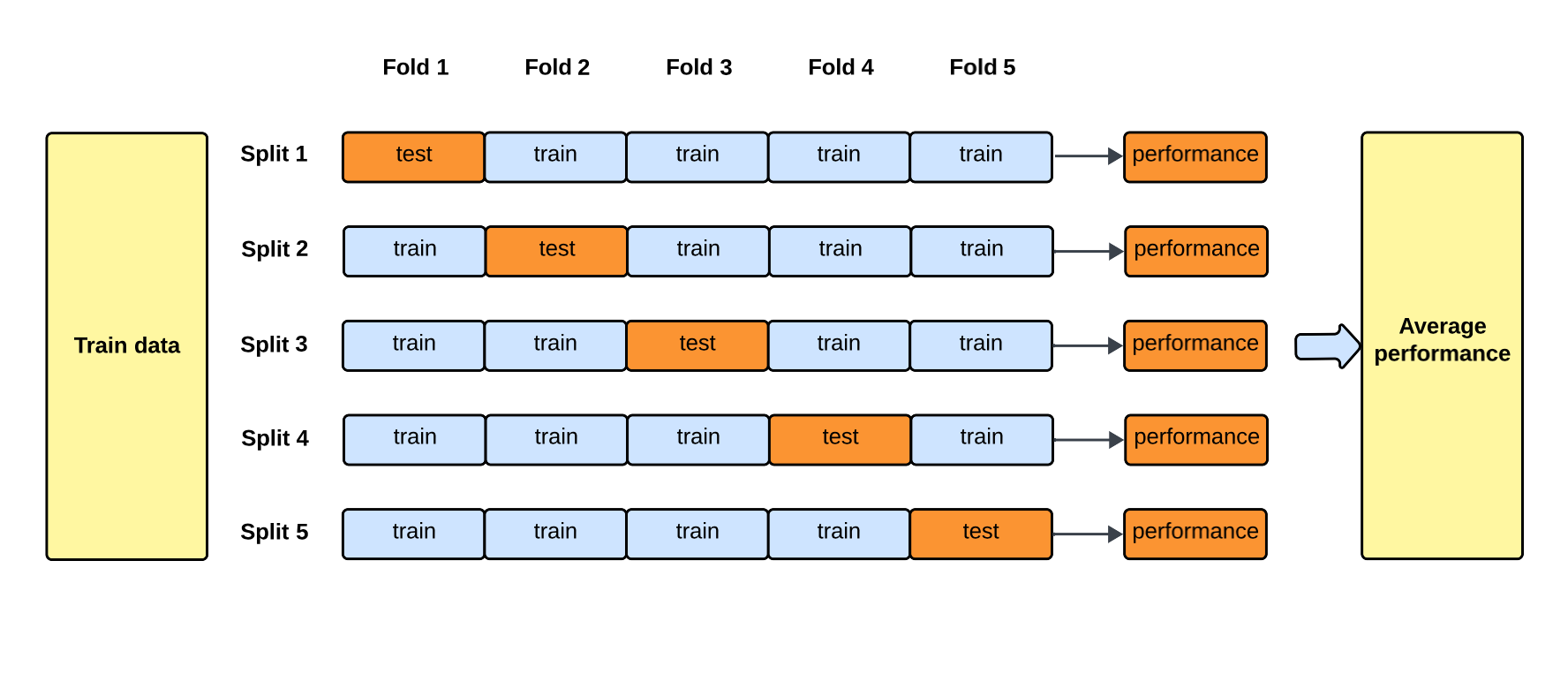
K-摺交叉驗證將原始訓練數據隨機分成 K 個大小相似的互斥子集（摺）。然後進行 K 次訓練和驗證：每次選擇其中 K-1 摺作為訓練集，剩下 1 摺作為驗證集。最終將 K 次驗證結果的平均值作為模型效能的評估。這種方法讓每個樣本都有機會被用作訓練數據和驗證數據，更充分地利用了數據，得到的效能評估結果比單次劃分（如簡單的 Hold-out 法）更穩定、更可靠，減少了因數據劃分隨機性帶來的偏差。但其計算成本相對較高（需要訓練 K 次模型）。注意，交叉驗證通常用於在訓練/驗證階段選擇超參數或比較模型，最終模型仍需在獨立的測試集上評估泛化能力。
#8
★★★★★
當一個機器學習模型在訓練集上表現極好，但在新的、未見過的數據（如測試集）上表現很差時，這種現象稱為？
A
欠擬合（Underfitting）
B
過擬合（Overfitting）
C
高偏差（High Bias）
D
低變異（Low Variance）
答案解析
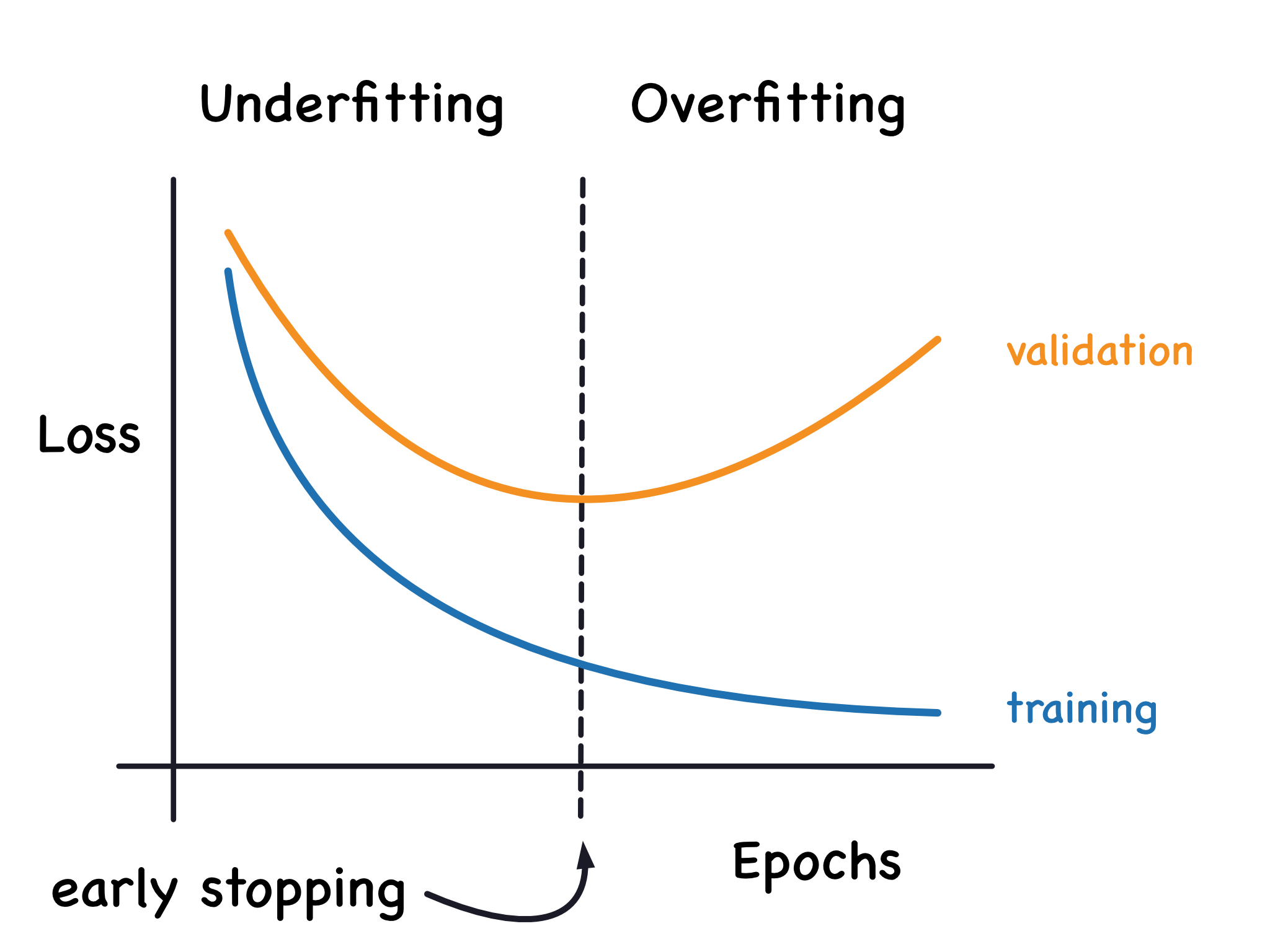
過擬合是指模型過度學習了訓練數據中的細節和雜訊，以至於失去了對數據普遍規律的捕捉能力，導致其泛化能力下降。表現為模型在訓練集上誤差很小，但在驗證集或測試集上誤差很大。這通常發生在模型過於複雜（相對於數據量或問題複雜度）或訓練時間過長時。相對地，欠擬合（Underfitting）是指模型過於簡單，未能充分學習訓練數據中的模式，導致在訓練集和測試集上表現都不好，通常對應高偏差（High Bias）。過擬合通常對應高變異（High Variance）。
#9
★★★★
以下哪種方法通常有助於緩解模型的過擬合（Overfitting）問題？
A
增加模型複雜度（例如增加神經網路層數或決策樹深度）
B
減少訓練數據量
C
使用正規化（Regularization）技術，如 L1 或 L2 正規化
D
訓練更長的時間
答案解析
緩解過擬合的方法主要有：
  1. 增加訓練數據量：讓模型看到更多樣例，減少對特定雜訊的記憶。
  2. 降低模型複雜度：使用更簡單的模型結構（如減少層數、節點數、特徵數）。
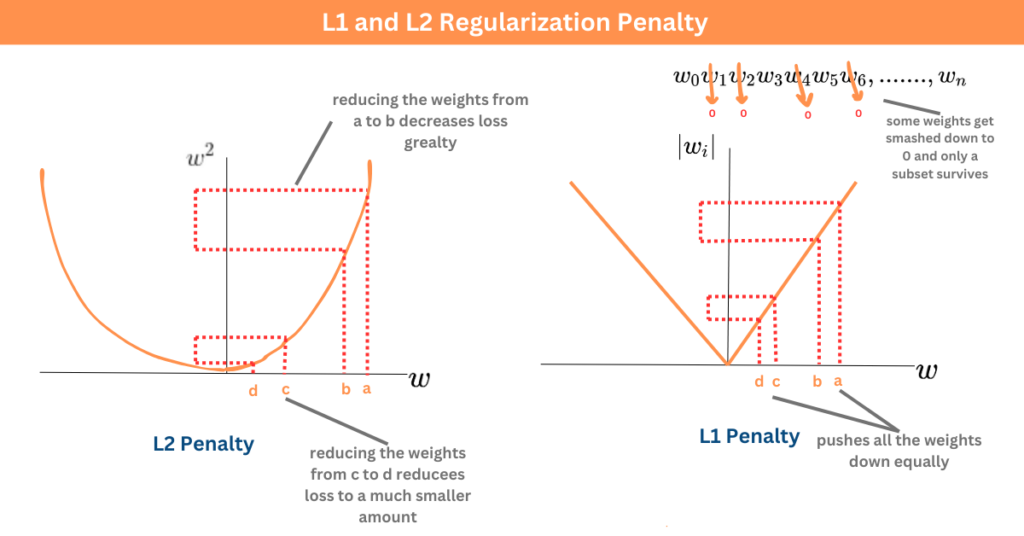
  3. 正規化（Regularization）：在損失函數中加入對模型參數的懲罰項（如 L1/L2 範數），限制模型參數的大小，使其更平滑，降低複雜度。
  4. Dropout：在神經網路訓練中隨機停用一部分神經元，減少神經元之間的協同適應。
  5. 早期停止（Early Stopping）：在驗證集效能不再提升時停止訓練。
選項 A 和 D 通常會加劇過擬合。選項 B 會使過擬合更容易發生。選項 C（正規化）是常用的防止過擬合的技術。
#10
★★★★
對於特徵維度非常高（例如文本數據的 TF-IDF 特徵）且數據線性可分或近似線性可分的問題，哪種模型通常表現較好且計算效率較高？
A
K-近鄰（K-Nearest Neighbors, KNN）
B
線性支持向量機（Linear Support Vector Machine, Linear SVM）或邏輯回歸（Logistic Regression）
C
決策樹（Decision Tree）
D
帶有非線性核函數的支持向量機（Non-linear SVM with Kernels）
答案解析
在高維稀疏數據（如文本 TF-IDF 特徵）且問題本身線性可分性較好的情況下，線性模型（如線性 SVM、邏輯回歸）通常表現良好且訓練速度快。KNN 在高維空間中計算距離成本高且效果易受維度災難影響。決策樹容易過擬合高維數據，且對線性關係捕捉不直接。非線性 SVM 雖然能處理非線性問題，但在特徵維度已經非常高的情況下，其計算複雜度（尤其涉及核函數計算）可能很高，且如果數據本身線性可分性好，則不一定比線性模型更有優勢。
#11
★★★★
隨機森林（Random Forest）相比於單個決策樹（Decision Tree）的主要優勢是？
A
模型解釋性更強
B
通常具有更好的泛化能力，不易過擬合
C
訓練速度更快
D
只需要更少的記憶體
答案解析
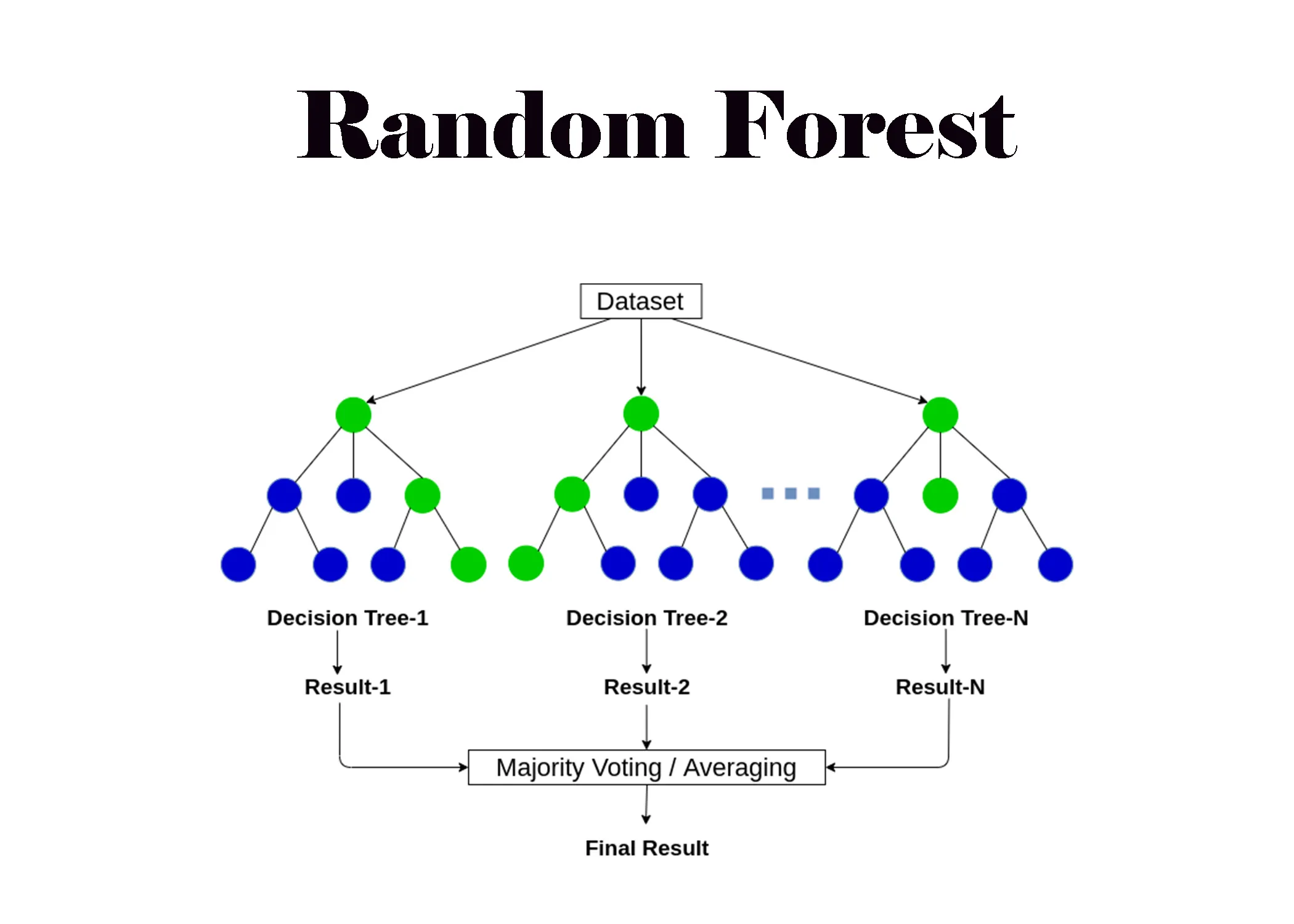
隨機森林是一種集成學習（Ensemble Learning）方法，它透過構建多個決策樹並將它們的預測結果進行整合（分類問題用投票，回歸問題用平均）來做出最終預測。其核心思想是「隨機化」：1. 透過自助採樣（Bootstrap Sampling）為每棵樹隨機抽取訓練樣本；2. 在每個節點分裂時，只從隨機抽取的部分特徵中選擇最佳分裂點。這兩個隨機性使得每棵樹之間具有差異性，降低了模型整體的變異（Variance），從而有效減少了單個決策樹容易過擬合的問題，提高了模型的穩定性和泛化能力。缺點是模型解釋性不如單棵樹，且訓練和預測通常比單棵樹慢。
#12
★★★★★
在二元分類問題中，當我們更關心「所有被模型預測為正類的樣本中，實際為正類的比例」時，應該關注哪個評估指標？
A
準確率（Accuracy）
B
精確率（Precision）
C
召回率（Recall）/ 敏感度（Sensitivity）
D
F1 分數（F1 Score）
答案解析
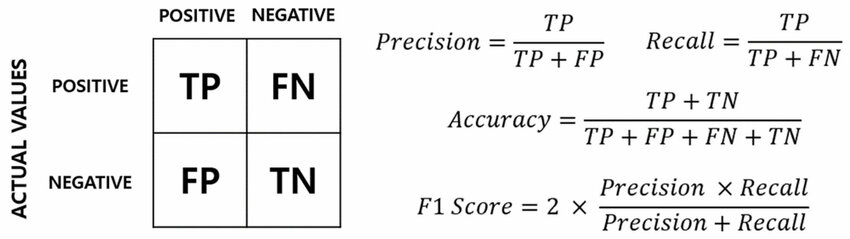
精確率（Precision）的定義是 TP / (TP + FP)，其中 TP (True Positive) 是真正例，FP (False Positive) 是假正例。它衡量的是在所有被模型預測為正類（TP + FP）的樣本中，有多少是真正為正類（TP）的。換句話說，它關注預測結果的「準確性」，即模型預測為正類的可信度有多高。例如，在垃圾郵件檢測中，高精確率意味著被標記為垃圾郵件的郵件中，很少有正常郵件被誤判。召回率（Recall）= TP / (TP + FN)，關注的是所有實際為正類的樣本中，有多少被模型成功找出來了。準確率是整體預測正確的比例。F1分數是精確率和召回率的調和平均數。
#13
★★★★★
在二元分類問題中，當我們更關心「所有實際為正類的樣本中，有多少被模型成功預測出來」時，應該關注哪個評估指標？
A
準確率（Accuracy）
B
精確率（Precision）
C
召回率（Recall）/ 敏感度（Sensitivity）
D
F1 分數（F1 Score）
答案解析
召回率（Recall），也稱為敏感度（Sensitivity）或真正例率（True Positive Rate, TPR），其定義是 TP / (TP + FN)，其中 TP 是真正例，FN (False Negative) 是假負例。它衡量的是在所有實際為正類（TP + FN）的樣本中，有多少被模型成功地預測為正類（TP）。換句話說，它關注預測結果的「完整性」或「查全率」，即模型找出所有正類樣本的能力。例如，在疾病篩檢中，高召回率意味著能夠找出絕大多數真正患病的病人，減少漏診。
#14
★★★
主成分分析（Principal Component Analysis, PCA）是一種常用的特徵工程技術，其主要目的是？
A
選擇與目標變數最相關的特徵子集
B
將原始高維特徵轉換為一組線性不相關的低維特徵（主成分），同時盡可能保留原始數據的變異性
C
將類別特徵轉換為數值特徵
D
填補數據中的缺失值
答案解析
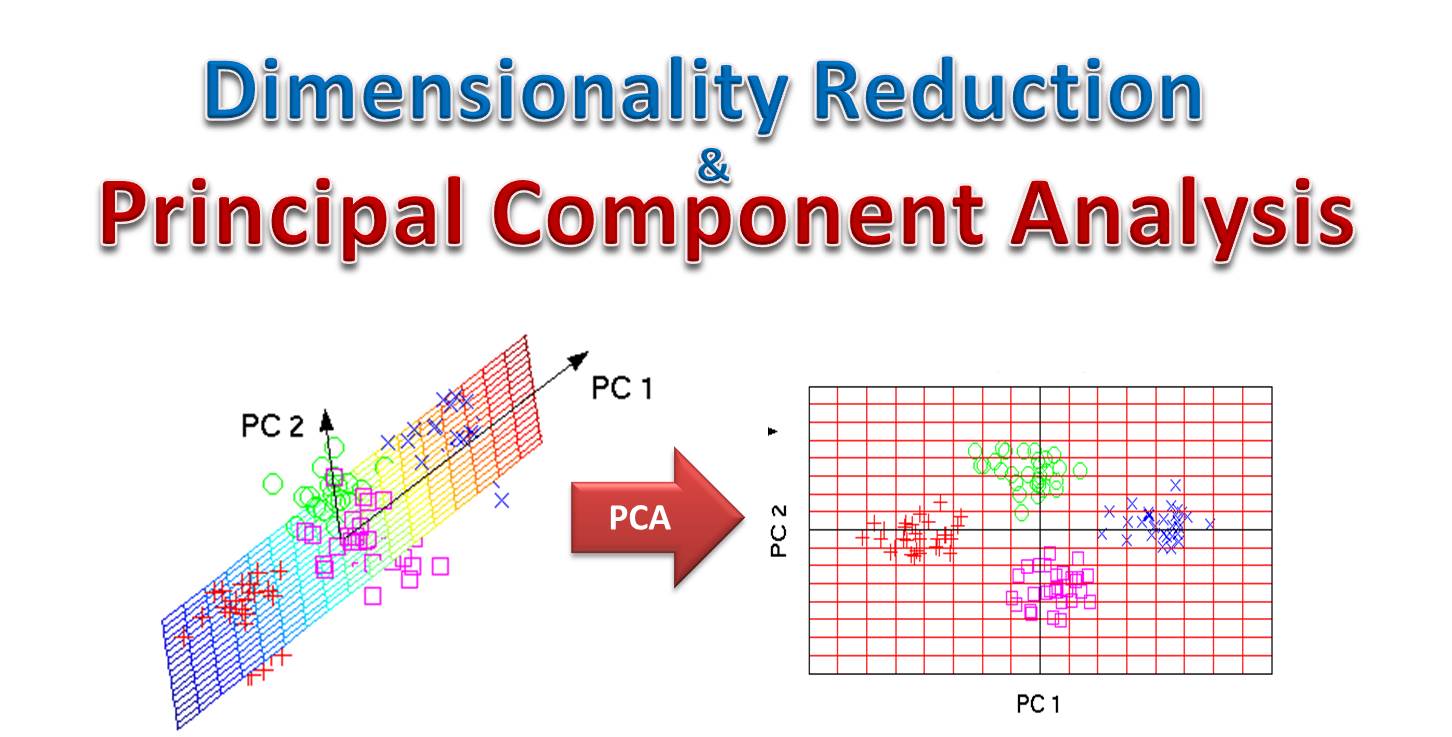
PCA 是一種無監督的降維技術。它透過線性變換，將原始的 P 個可能相關的特徵轉換為 K 個（K <= P）稱為主成分的新特徵。這些主成分是按照它們能夠解釋原始數據變異量的大小來排序的，並且彼此之間線性不相關（正交）。透過選擇變異量最大的前 K 個主成分，可以在降低數據維度的同時，最大程度地保留原始數據的主要資訊。PCA常用於數據視覺化、去除冗餘特徵、降低計算複雜度等。它不考慮目標變數（選項A描述的是特徵選擇方法）。
#15
★★★
處理數據中的離群值（Outliers）時，以下哪種方法比較穩健（Robust），不易受極端值影響？
A
使用平均數（Mean）進行統計分析或填補
B
使用中位數（Median）或四分位距（Interquartile Range, IQR）進行分析或檢測
C
直接刪除所有看起來異常的數值
D
使用標準差（Standard Deviation）進行檢測（如 3σ 法則）
答案解析
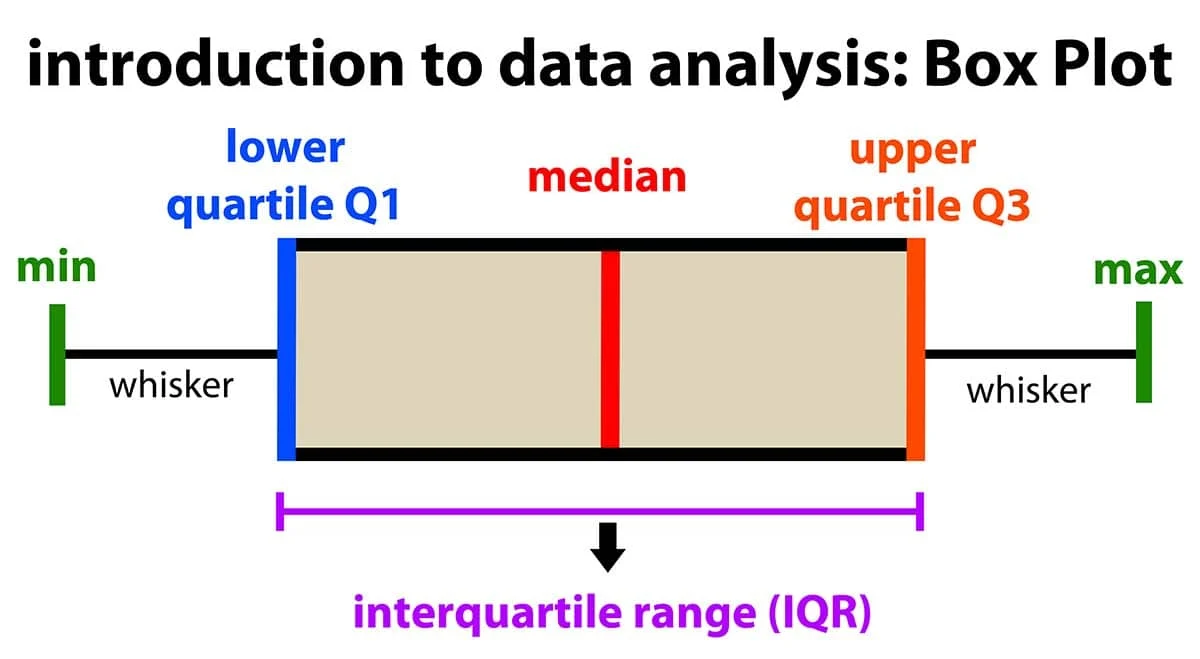
離群值是數據中遠離大部分數據點的數值。平均數和標準差都容易受到極端值的影響而發生劇烈變化。相比之下，中位數（排序後位於中間的值）和四分位距（IQR = Q3 - Q1，即第75百分位數與第25百分位數之差）對極端值的敏感度較低，是更穩健的統計量。因此，在存在離群值時，使用中位數進行填補或使用基於IQR的方法（如檢測超出 Q1 - 1.5*IQR 或 Q3 + 1.5*IQR 範圍的值）來識別離群值通常更可靠。直接刪除異常值（C）可能丟失重要資訊，需謹慎。
#16
★★★
模型的「偏差」（Bias）指的是什麼？
A
模型預測結果對於訓練數據變化的敏感度
B
模型預測值與真實值之間的系統性差異，通常源於模型假設過於簡化
C
訓練數據中的雜訊量
D
模型在測試集上的錯誤率
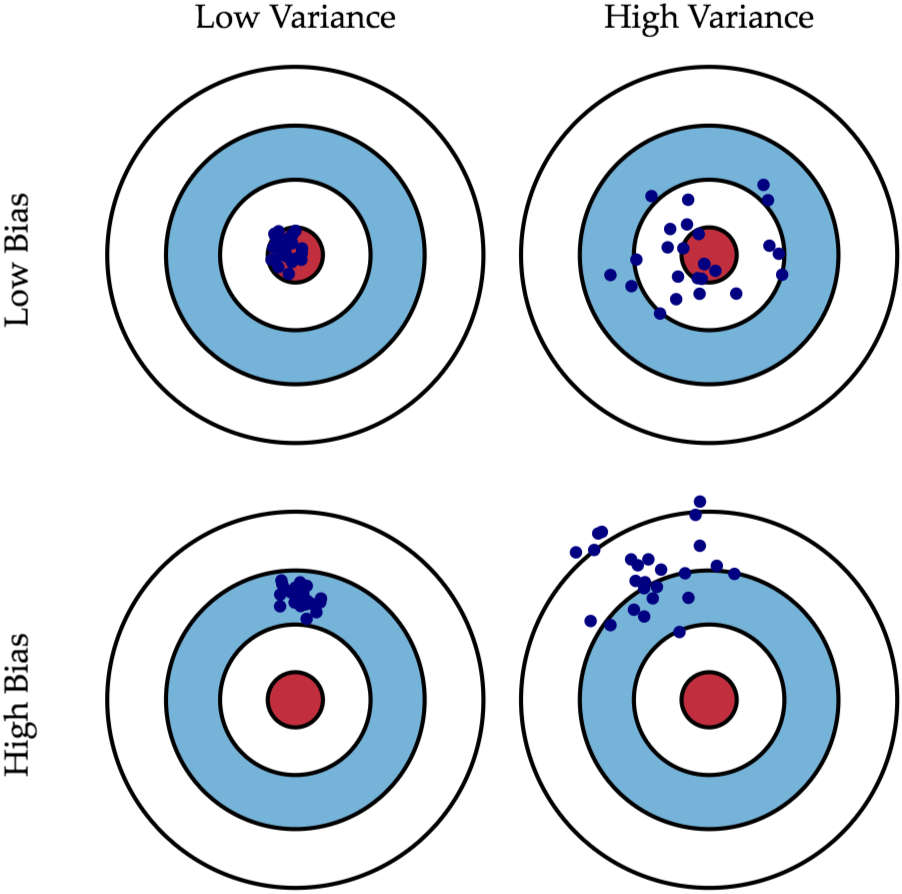
答案解析
偏差衡量的是模型的預測結果與真實結果之間的期望差距，反映了模型本身的擬合能力。高偏差通常意味著模型過於簡單，未能捕捉到數據中的複雜模式（欠擬合），導致其預測系統性地偏離真實值。例如，試圖用線性模型去擬合非線性數據。選項A描述的是模型的「變異」（Variance）。
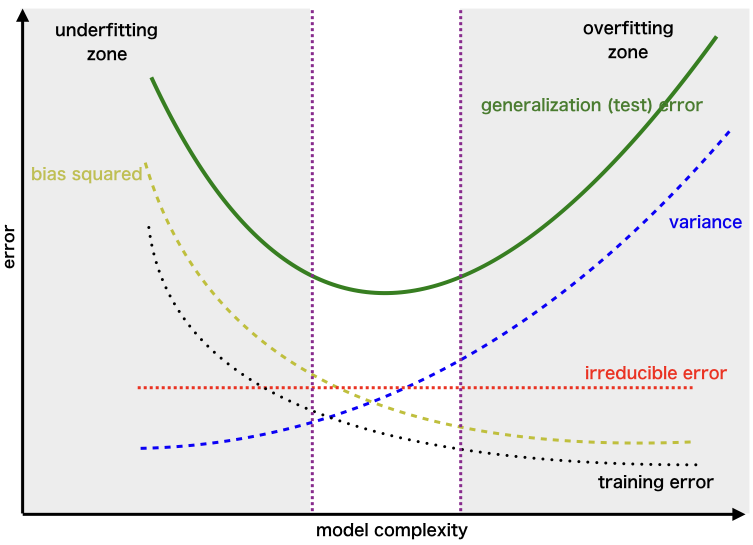
#17
★★★
模型的「變異」（Variance）指的是什麼？
A
模型預測結果對於訓練數據集微小變化的敏感度
B
模型預測值與真實值之間的系統性差異
C
模型所需的訓練時間
D
模型參數的數量
答案解析
變異衡量的是如果使用不同的訓練數據集來訓練模型，模型預測結果會有多大的波動。高變異通常意味著模型過於複雜，對訓練數據中的雜訊或特定模式過度敏感（過擬合）。這樣的模型在不同的訓練數據集上可能產生差異很大的預測結果，泛化能力差。例如，一個非常深的決策樹或高度擬合的多項式回歸。選項B描述的是模型的「偏差」（Bias）。
#18
★★★
梯度提升決策樹（Gradient Boosting Decision Tree, GBDT）與隨機森林（Random Forest）的主要區別在於？
A
隨機森林是線性模型，GBDT是非線性模型
B
隨機森林中的樹是獨立、平行構建的；GBDT中的樹是依次、串行構建的，後面的樹旨在修正前面樹的錯誤
C
隨機森林只能用於分類，GBDT只能用於回歸
D
GBDT比隨機森林更不容易過擬合
答案解析
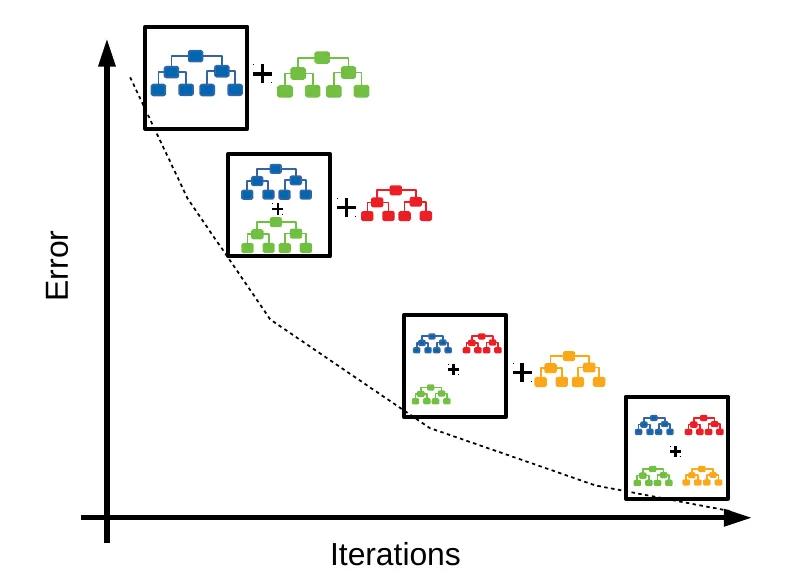
兩者都是基於決策樹的集成學習方法，但構建方式不同。隨機森林採用 Bagging 思想，透過自助採樣和隨機特徵選擇構建多個獨立的樹，然後平行地訓練這些樹，最後透過投票或平均來整合結果，主要目標是降低變異。GBDT 採用 Boosting 思想，它依次、串行地構建樹，每一棵新樹都試圖擬合前面所有樹組合起來的殘差（Residual）或梯度，逐步修正模型的預測誤差，主要目標是降低偏差。因此，GBDT 的樹之間是有依賴關係的。兩者都可以用於分類和回歸。GBDT 對超參數更敏感，更容易過擬合，但調整得當時通常能達到比隨機森林更高的精度。
#19
★★★★
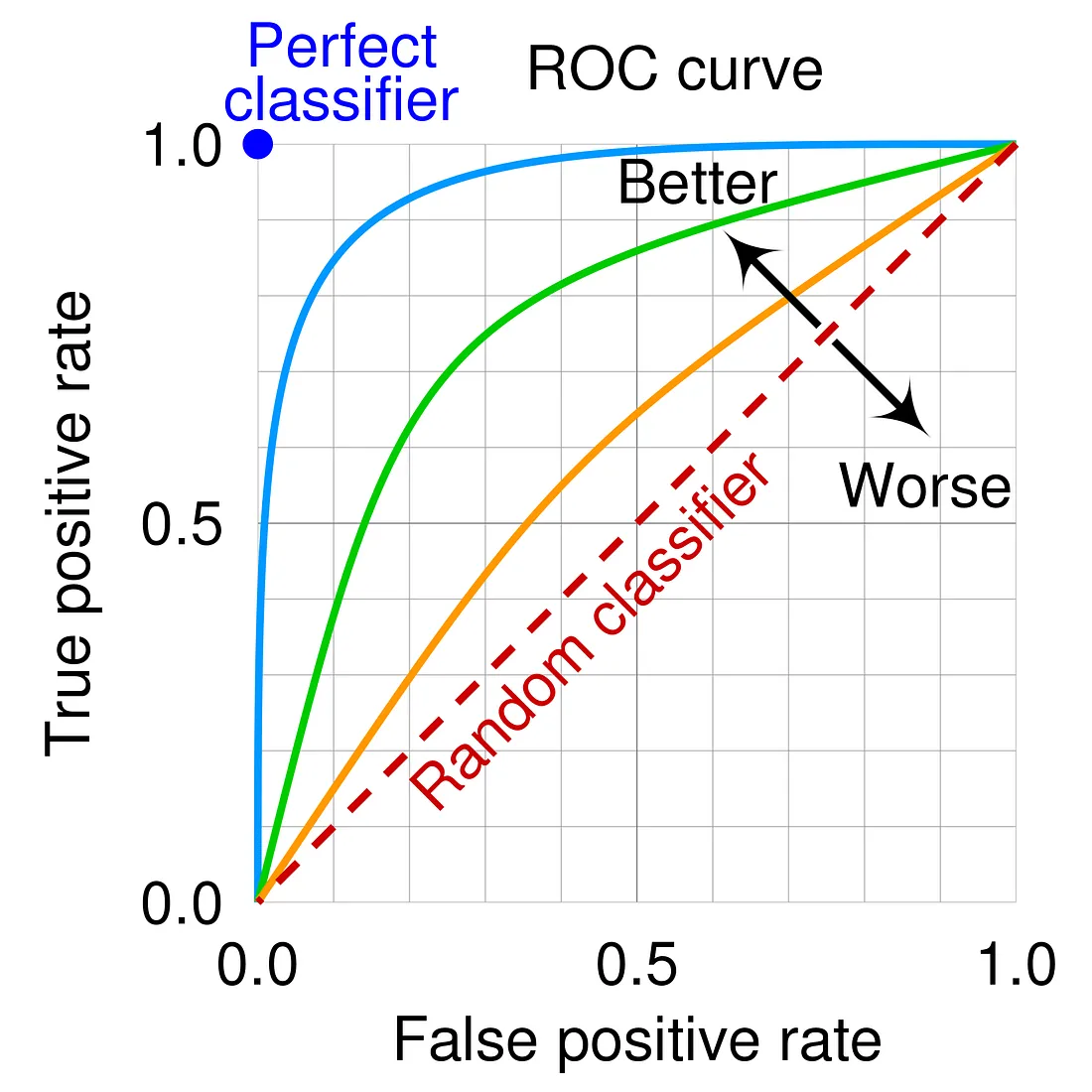
ROC 曲線（Receiver Operating Characteristic Curve）是以哪兩個指標為座標軸繪製的？
A
精確率（Precision） vs. 召回率（Recall）
B
真正例率（True Positive Rate, TPR） vs. 假正例率（False Positive Rate, FPR）
C
準確率（Accuracy） vs. 模型複雜度
D
訓練誤差 vs. 驗證誤差
答案解析
ROC 曲線是評估二元分類模型效能的重要工具，特別是在不同分類閾值（Threshold）下的表現。它的橫座標是假正例率（False Positive Rate, FPR），計算公式為 FP / (FP + TN)，表示實際為負類的樣本中被錯誤預測為正類的比例。縱座標是真正例率（True Positive Rate, TPR），即召回率（Recall）或敏感度（Sensitivity），計算公式為 TP / (TP + FN)，表示實際為正類的樣本中被正確預測為正類的比例。ROC 曲線下的面積（Area Under the Curve, AUC）是一個常用的匯總指標，AUC 越接近 1，表示模型區分正負類的能力越強。選項A描述的是 Precision-Recall 曲線。
#20
★★★
對於具有時間序列特性的數據（例如股票價格、感測器讀數），在劃分訓練集和測試集時，最應避免的做法是？
A
按照時間順序，將較早的數據作為訓練集，較晚的數據作為測試集
B
完全隨機地從所有數據中抽取樣本作為訓練集和測試集
C
使用滾動窗口（Rolling Window）或擴展窗口（Expanding Window）的方式進行驗證
D
確保測試集的時間點都在訓練集之後
答案解析
時間序列數據具有時間依賴性，即當前的數值可能與過去的數值相關。在現實應用中，我們通常是利用過去的數據來預測未來。如果在劃分數據集時進行完全隨機抽樣（B），會導致訓練集中包含未來的數據，而測試集中包含過去的數據，這違反了時間順序，使得模型在訓練時「看到」了未來資訊，導致評估結果過於樂觀，無法真實反映模型在預測未來時的表現（產生數據洩漏）。正確的做法是保持時間順序，例如將早期數據用於訓練，晚期數據用於測試（A、D），或者使用更複雜的時間序列交叉驗證方法如滾動/擴展窗口（C）。
#21
★★★
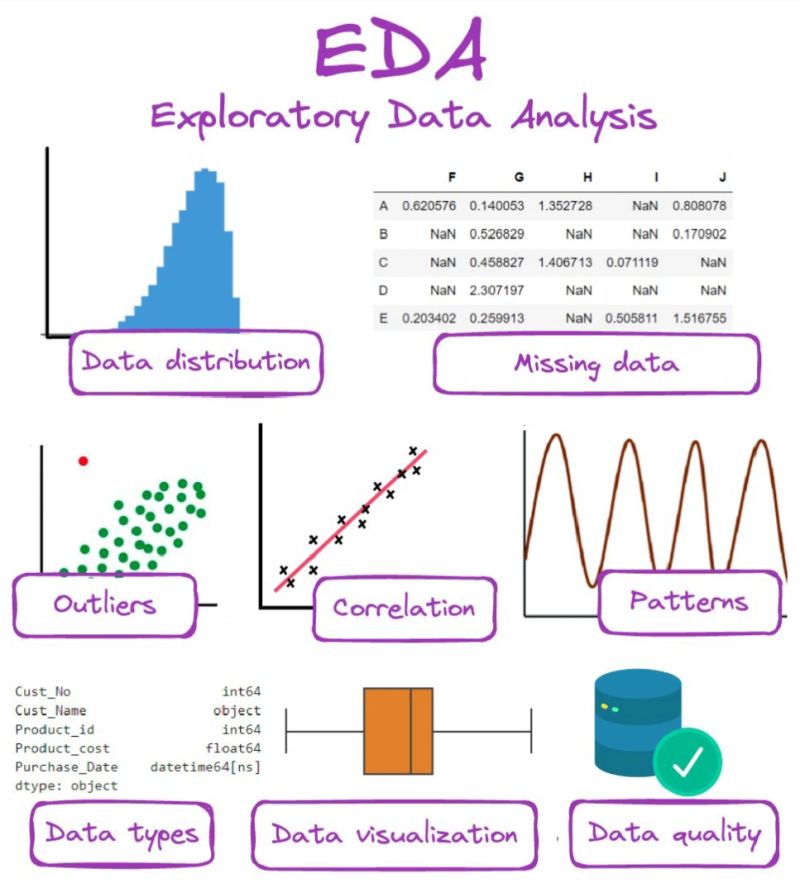
探索性數據分析（Exploratory Data Analysis, EDA）的主要目的是什麼？
A
直接訓練出最終模型
B
透過視覺化和統計摘要來理解數據的主要特徵、分佈、關係和潛在問題
C
評估模型的預測準確率
D
將模型部署到生產環境
答案解析
EDA 是在進行正式的建模之前，對數據進行初步探索和理解的過程。它通常涉及使用各種視覺化工具（如直方圖、散點圖、箱形圖）和描述性統計量（如平均數、中位數、標準差、相關係數）來檢查數據的分佈情況、變數之間的關係、是否存在異常值或缺失值、數據的整體結構等。EDA 的目的是獲得對數據的直觀感受，發現潛在的模式和問題，為後續的數據清理、特徵工程和模型選擇提供依據和方向。
#22
★★★
假設你有一個「客戶流失預測」的數據集，其中包含「上次購買日期」這個欄位，為了讓模型能更好地利用這個資訊，可以進行哪種特徵工程？
A
直接將日期作為字串輸入模型
B
計算「距離現在的天數」（Recency）、提取「星期幾」、「月份」等衍生特徵
C
將日期轉換為獨熱編碼
D
刪除這個欄位
答案解析
日期或時間戳欄位通常不能直接作為數值或類別特徵輸入模型。需要進行特徵工程，提取其中有意義的資訊。對於「上次購買日期」，可以計算與當前日期（或數據收集截止日期）的時間差，得到「最近一次購買間隔」（Recency），這通常與客戶流失風險密切相關。此外，還可以提取日期中的周期性成分，如購買發生在星期幾、月份、是否為假日等，這些可能也與客戶行為模式有關。這些衍生出來的新特徵更能被模型所理解和利用。直接使用字串（A）或獨熱編碼（C，會導致維度爆炸）通常效果不佳。刪除欄位（D）則會丟失重要資訊。
#23
★★★
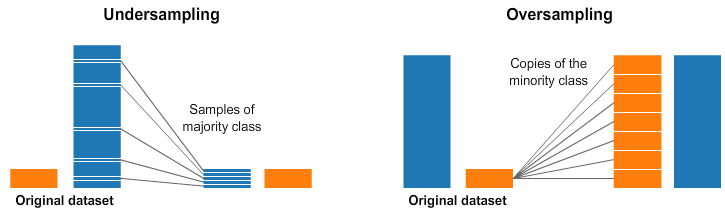
在處理類別不平衡（Class Imbalance）的數據集時（例如，欺詐檢測中欺詐樣本遠少於正常樣本），下列哪種做法可能會有幫助？
A
只使用準確率（Accuracy）作為評估指標
B
採用過採樣（Oversampling）少數類別或欠採樣（Undersampling）多數類別，或使用如 SMOTE 等合成數據生成技術
C
忽略類別不平衡問題，直接訓練標準模型
D
將所有少數類別樣本從數據集中移除
答案解析
類別不平衡會導致模型傾向於預測多數類別，使得在少數類別上的效能很差。只看準確率（Accuracy）會產生誤導，因為即使模型將所有樣本都預測為多數類別，準確率仍然可能很高。處理方法包括：
  1. 數據層面：透過過採樣（複製少數類別樣本）、欠採樣（刪除多數類別樣本）或 SMOTE（Synthetic Minority Over-sampling Technique，合成新的少數類別樣本）等方法來平衡數據集。
  2. 演算法層面：選擇對不平衡數據不敏感的模型，或在模型訓練時調整類別權重（給予少數類別更高的錯誤懲罰）。
  3. 評估指標：使用 Precision, Recall, F1-score, AUC, PR曲線 等對不平衡更敏感的指標來評估模型。
選項 B 描述了數據層面的常用處理方法。
#24
★★★
理想的機器學習模型應該具有什麼樣的偏差（Bias）和變異（Variance）？
A
高偏差，高變異
B
高偏差，低變異
C
低偏差，高變異
D
低偏差，低變異
答案解析
偏差和變異是模型泛化誤差的兩個主要來源，通常存在一種權衡（Trade-off）關係。
  • 低偏差意味著模型能夠很好地擬合數據，預測值接近真實值。
  • 低變異意味著模型對訓練數據的變化不敏感，表現穩定。
理想的模型是能夠同時達到低偏差和低變異，即既能準確捕捉數據模式，又具有良好的穩定性和泛化能力。高偏差低變異對應欠擬合。低偏差高變異對應過擬合。高偏差高變異則表示模型既沒學好也對數據敏感，是最差情況。
#25
★★★
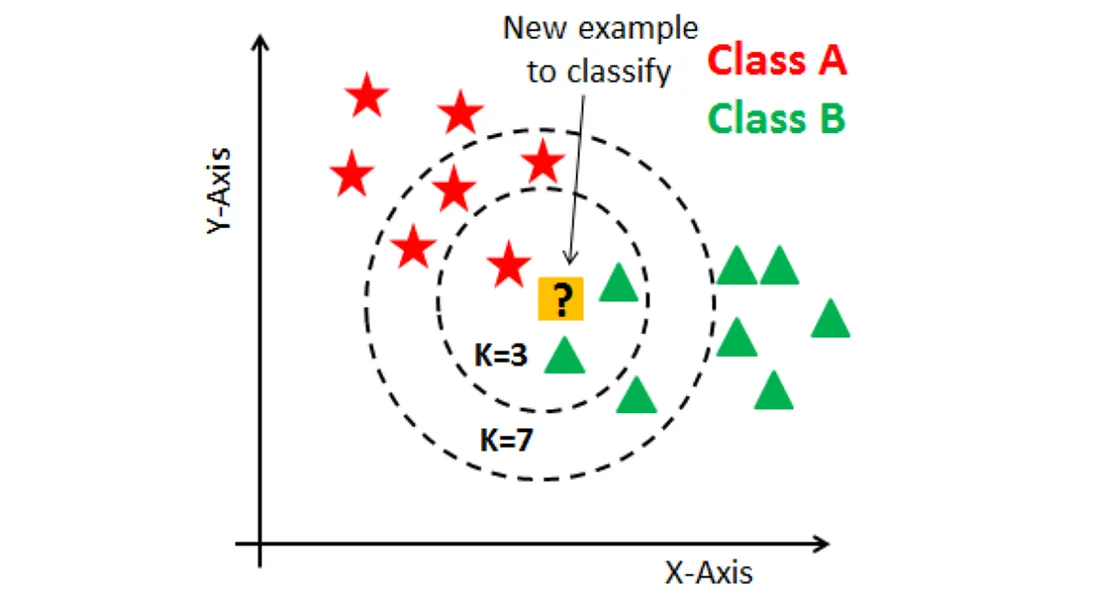
K-近鄰（K-Nearest Neighbors, KNN）演算法的主要缺點之一是？
A
模型訓練階段非常耗時
B
預測階段計算成本高，對數據量和特徵維度敏感
C
只能處理線性可分問題
D
模型解釋性差
答案解析
KNN 是一種基於實例的學習（Instance-based Learning）或懶惰學習（Lazy Learning）演算法。它在訓練階段幾乎不做任何事情，只是將訓練數據儲存起來。主要的計算發生在預測階段：對於一個新的輸入樣本，它需要計算該樣本與所有訓練樣本之間的距離，找出距離最近的 K 個鄰居，然後根據這些鄰居的標籤進行投票（分類）或平均（回歸）來得到預測結果。因此，當訓練數據量很大或特徵維度很高時，預測階段的計算成本會非常高，效率低下。這也使得 KNN 對特徵尺度敏感，且在高維空間中效果可能下降（維度災難）。
#26
★★★
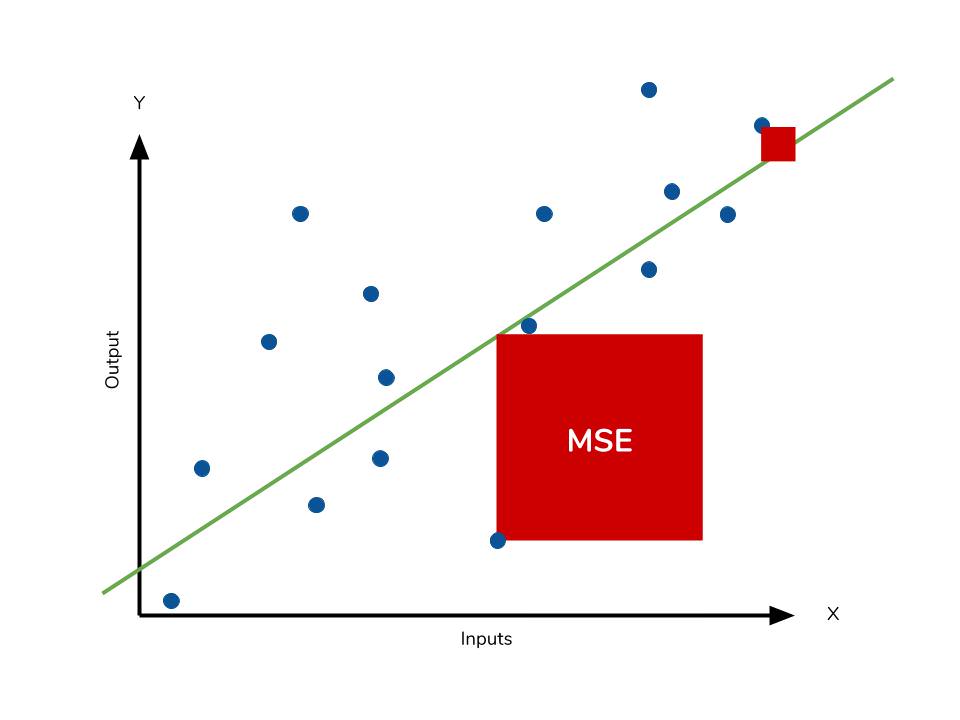
在回歸問題中，均方誤差（Mean Squared Error, MSE）衡量的是什麼？
A
模型預測正確的樣本比例
B
預測值與真實值之差的平方的平均值
C
預測值與真實值之差的絕對值的平均值
D
模型能夠解釋的目標變數變異量的比例
答案解析
MSE 是評估回歸模型效能最常用的指標之一。它計算的是每個樣本的預測值 (ŷ) 與真實值 (y) 之差的平方，然後再對所有樣本取平均值。公式為 MSE = (1/n) * Σ(yᵢ - ŷᵢ)²。MSE 對較大的誤差給予更高的權重（因為是平方），其單位是目標變數單位的平方。數值越小表示模型預測越準確。選項A是準確率（分類指標）。選項C是平均絕對誤差（Mean Absolute Error, MAE）。選項D是決定係數（R-squared）。
#27
★★
數據清洗中，處理重複記錄（Duplicate Records）的常見做法是？
A
保留所有重複記錄
B
識別並移除重複的記錄，只保留一份
C
將重複記錄的數值取平均
D
為重複記錄創建新的標籤
答案解析
重複記錄是指數據集中存在內容完全相同或幾乎相同的多筆記錄。它們可能是由於數據收集錯誤、系統故障或數據合併不當等原因產生的。保留重複記錄會導致模型在訓練時對這些記錄過度加權，可能引入偏差並影響模型效能評估的準確性。因此，常見的做法是在數據清洗階段識別出這些重複記錄，並根據業務邏輯決定如何處理，最常見的是直接移除多餘的重複項，只保留其中一份記錄。
#28
★★★
最小最大縮放（Min-Max Scaling）將特徵數值轉換到哪個範圍？
A
平均數為 0，標準差為 1
B
通常是 [0, 1] 或 [-1, 1]
C
任意範圍，取決於原始數據
D
只包含整數
答案解析
最小最大縮放，也常被稱為正規化（Normalization），是一種將數值特徵線性地縮放到一個特定範圍的預處理技術。最常見的目標範圍是 [0, 1]。其計算公式為 (X - X_min) / (X_max - X_min)，其中 X_min 和 X_max 分別是該特徵的最小值和最大值。這種方法可以保留原始數據的相對關係，但對離群值非常敏感（離群值會決定最大或最小值，壓縮其他數據的範圍）。選項A描述的是標準化（Standardization）。
#29
★★
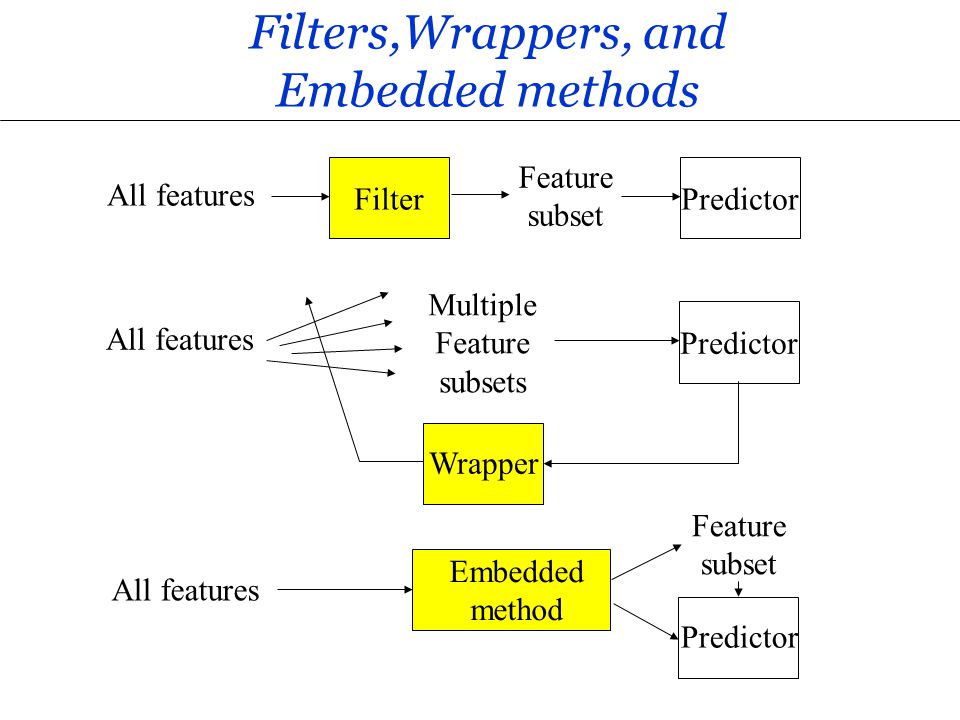
在特徵選擇（Feature Selection）中，過濾法（Filter Methods）的主要特點是？
A
使用特定機器學習模型的效能來評估特徵子集
B
獨立於任何機器學習演算法，僅根據特徵本身的統計特性（如相關性、變異數）來進行評分和排序
C
將特徵選擇過程嵌入到模型訓練過程中
D
總是能選出最佳的特徵組合
答案解析
特徵選擇旨在從原始特徵集中選出一個子集，以提高模型效能、降低複雜度或改善可解釋性。過濾法是最簡單的一類方法，它在模型訓練之前進行，獨立於後續使用的學習演算法。它通常計算每個特徵與目標變數之間的某種統計指標（如相關係數、卡方檢定、資訊增益等）或特徵本身的屬性（如低變異數），然後根據這些指標對特徵進行排序或設定閾值來選擇特徵。優點是計算速度快，不易過擬合；缺點是沒有考慮特徵之間的組合效應以及與特定模型的交互作用。選項A描述的是封裝法（Wrapper Methods）。選項C描述的是嵌入法（Embedded Methods）。
#30
★★
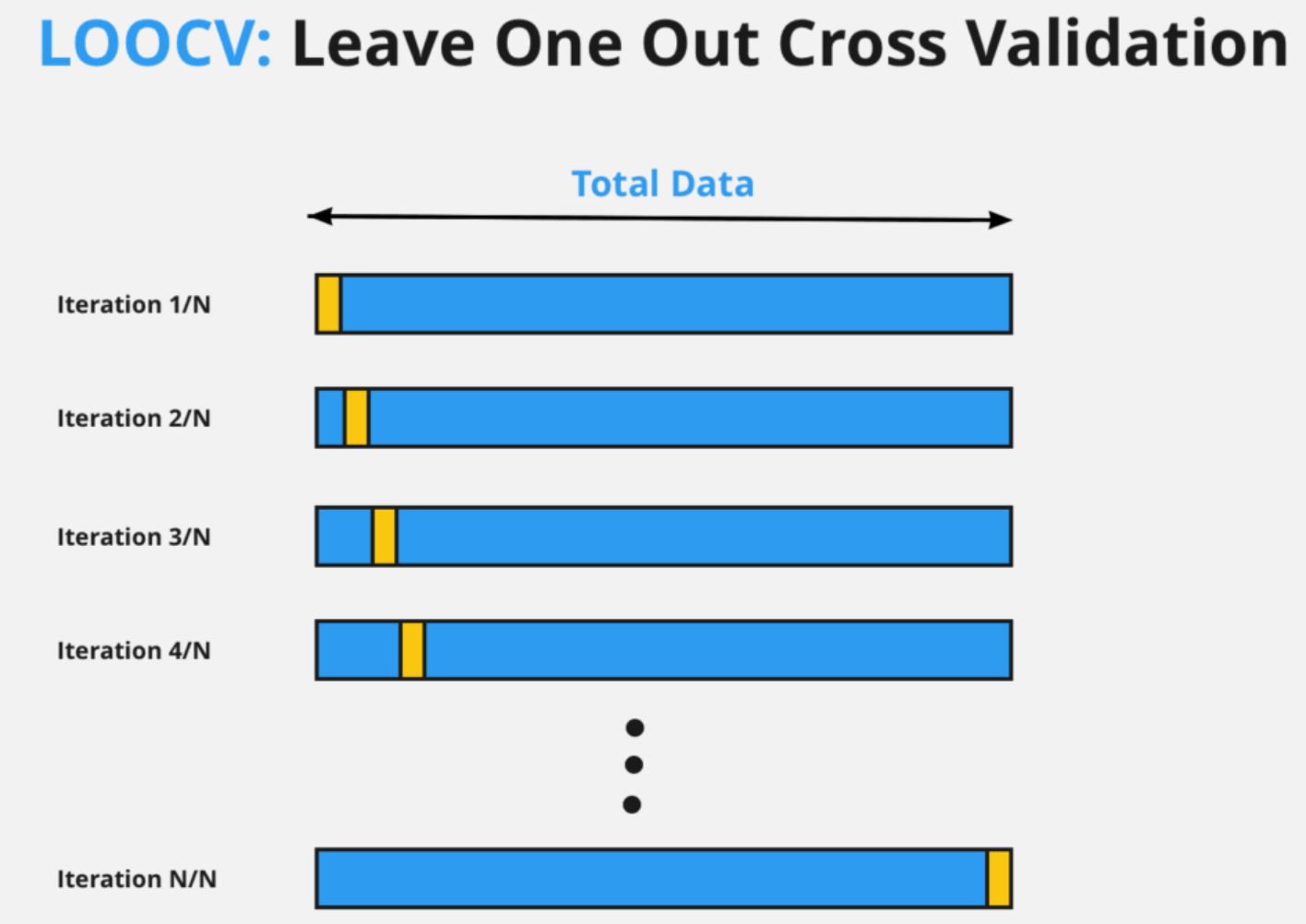
當數據量非常有限時，哪種交叉驗證方法可以最大程度地利用數據進行訓練和驗證？
A
簡單的 Hold-out 法（劃分一次訓練集和驗證集）
B
留一交叉驗證（Leave-One-Out Cross-Validation, LOOCV）
C
3-摺交叉驗證（3-Fold Cross-Validation）
D
重複隨機子抽樣驗證（Repeated Random Sub-sampling Validation）
答案解析
LOOCV 是 K-摺交叉驗證的一個特例，其中 K 等於樣本總數 N。也就是說，每次迭代時，只留下一個樣本作為驗證集，其餘 N-1 個樣本全部用於訓練。這個過程重複 N 次，每個樣本都被用作驗證集一次。這種方法最大限度地利用了數據進行訓練（每次訓練集大小為 N-1），因此在數據量非常少時，可以得到偏差較小的效能估計。但其缺點是計算成本非常高（需要訓練 N 次模型），且由於每次的訓練集都非常相似，估計結果的變異可能較大。
#31
★★★
欠擬合（Underfitting）通常發生在什麼情況下？
A
模型過於複雜
B
模型過於簡單，無法捕捉數據中的基本模式
C
訓練數據量過大
D
驗證集效能持續提升
答案解析
欠擬合是指模型未能充分學習訓練數據的結構和模式，導致模型在訓練集和測試集（或驗證集）上的表現都不佳。這通常是因為模型本身的假設過於簡化，其容量不足以擬合數據的複雜性。例如，試圖用線性模型去擬合高度非線性的數據。欠擬合對應著高偏差（High Bias）。
#32
★★★
決策樹（Decision Tree）模型的一個主要缺點是？
A
難以理解和解釋
B
容易對訓練數據產生過擬合，對數據的微小變動敏感
C
無法處理類別型特徵
D
訓練速度通常比深度學習模型慢
答案解析
單個決策樹模型，特別是未經剪枝（Pruning）的深度決策樹，非常容易過擬合訓練數據。它可以不斷地分裂節點，直到完美地劃分訓練集中的每個樣本，但這樣產生的複雜樹結構往往無法很好地泛化到新數據上。此外，決策樹的結構對訓練數據的微小變動（如增刪少量樣本）比較敏感，可能導致生成完全不同的樹。隨機森林等集成方法正是為了解決這個問題。決策樹的優點是模型直觀、易於解釋（A錯），且可以處理類別和數值特徵（C錯），訓練速度相對較快（D錯）。
#33
★★★★
F1 分數（F1 Score）的計算方式是？
A
精確率（Precision）和召回率（Recall）的算術平均數
B
精確率（Precision）和召回率（Recall）的調和平均數
C
精確率（Precision）和召回率（Recall）的幾何平均數
D
ROC 曲線下的面積（AUC）
答案解析
F1 分數是綜合考慮精確率（Precision）和召回率（Recall）的常用指標，特別是在類別不平衡或兩者都重要時。它是精確率和召回率的調和平均數（Harmonic Mean）。計算公式為 F1 = 2 * (Precision * Recall) / (Precision + Recall)。調和平均數的一個特性是，它更傾向於給予兩者中較小的值更大的影響力，只有當 Precision 和 Recall 都較高時，F1 分數才會高。這使得 F1 分數比簡單的算術平均數更能反映模型在兩方面的綜合表現。
#34
★★
結構化數據（Structured Data）通常指的是？
A
圖像、音訊、影片等非結構化內容
B
具有固定格式、易於組織和查詢的數據，通常存儲在資料庫表格中
C
自然語言文本
D
社交媒體貼文
答案解析
結構化數據是指具有預定義的數據模型或架構的數據，通常以表格形式組織，包含行和列，每列有明確定義的數據類型（如數值、字串、日期）。例如，關係型資料庫中的表格、Excel 試算表、CSV 文件等都屬於結構化數據。這種數據易於儲存、查詢和分析。相對地，非結構化數據（如圖像、音訊、影片、自由文本）沒有固定的格式。半結構化數據（如 JSON、XML）則介於兩者之間，具有一定的結構但不如表格數據嚴謹。
#35
★★★
在處理缺失值時，若缺失的模式並非完全隨機（例如，收入越高的人越不願意填寫收入），直接刪除缺失記錄或使用簡單填補（如平均數）可能會導致什麼問題？
A
完全解決缺失值問題
B
引入偏差（Bias），使得數據分析或模型訓練結果失真
C
增加數據的變異性
D
提高模型的泛化能力
答案解析
缺失值的模式主要有三種：完全隨機缺失（MCAR）、隨機缺失（MAR）和非隨機缺失（MNAR）。如果缺失是非隨機的（MNAR），即缺失本身與未觀察到的值有關（如收入越高越不填），那麼直接刪除缺失記錄會導致樣本選擇偏差，留下的樣本不再能代表整體。使用簡單填補（如平均數）則會忽略這種系統性的缺失模式，可能扭曲數據分佈和變數間的關係。這些都可能導致數據分析結果或模型訓練產生偏差，得出錯誤的結論。處理非隨機缺失通常需要更複雜的方法，如多重插補（Multiple Imputation）或建立模型來預測缺失值。
英文全名 機制 描述 範例 適用處理方法
MCAR
Missing Completely at Random		 完全隨機缺失 缺失與任何觀察到的或未觀察到的數據無關。 因技術故障導致調查回覆遺失。 列表刪除或平均數填補。
MAR
Missing at Random		 隨機缺失 缺失與觀察到的數據有關，但與缺失值本身無關。 男人披露收入的可能性較低，而女性的收入已被觀察到。 多重插補或模型基於填補。
MNAR
Missing Not at Random		 非隨機缺失 缺失與未觀察到的數據有關。 高膽固醇水平的人較不可能報告膽固醇。 進階方法如聯合建模或選擇建模。
#36
★★
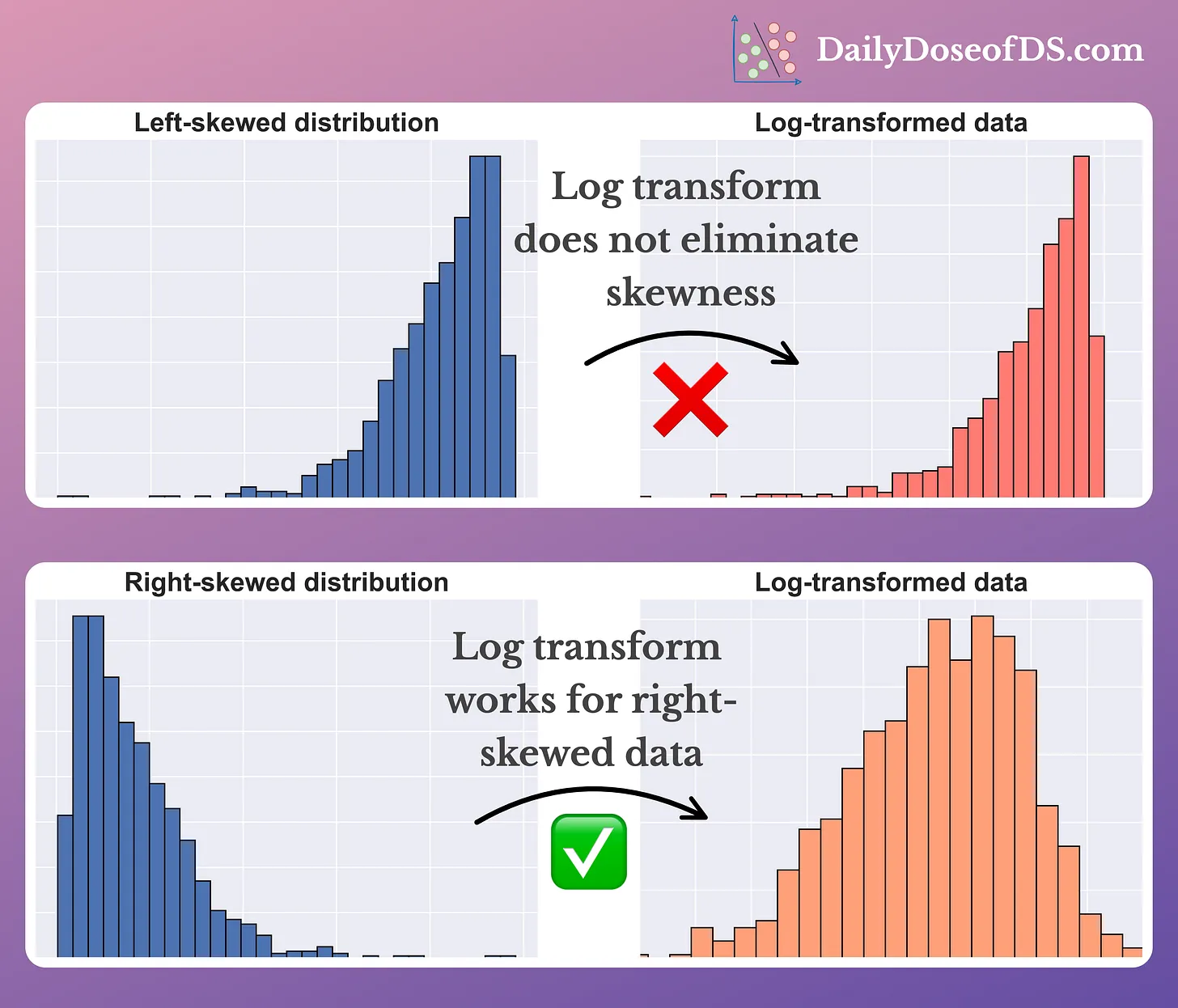
對於取值範圍非常廣且呈現偏態分佈（Skewed Distribution）的數值特徵（如收入、網站點擊次數），在輸入模型前，常進行哪種轉換來使其分佈更接近常態分佈？
A
獨熱編碼（One-Hot Encoding）
B
對數轉換（Log Transformation）
C
標準化（Standardization）
D
主成分分析（PCA）
答案解析
許多機器學習模型（特別是線性模型）假設特徵服從或接近常態分佈時表現更好。對於呈現右偏態（Right-skewed）分佈（長尾在右側，如收入）的數據，取其對數（通常是自然對數 log(x) 或 log(x+1) 以處理0值）可以有效地壓縮較大值的範圍，拉近數據點，使得轉換後的數據分佈更對稱，更接近常態分佈。這有助於穩定變異數，改善模型的擬合效果。其他可能的轉換還有平方根轉換等。標準化（C）只改變均值和標準差，不改變分佈形狀。
#37
★★★
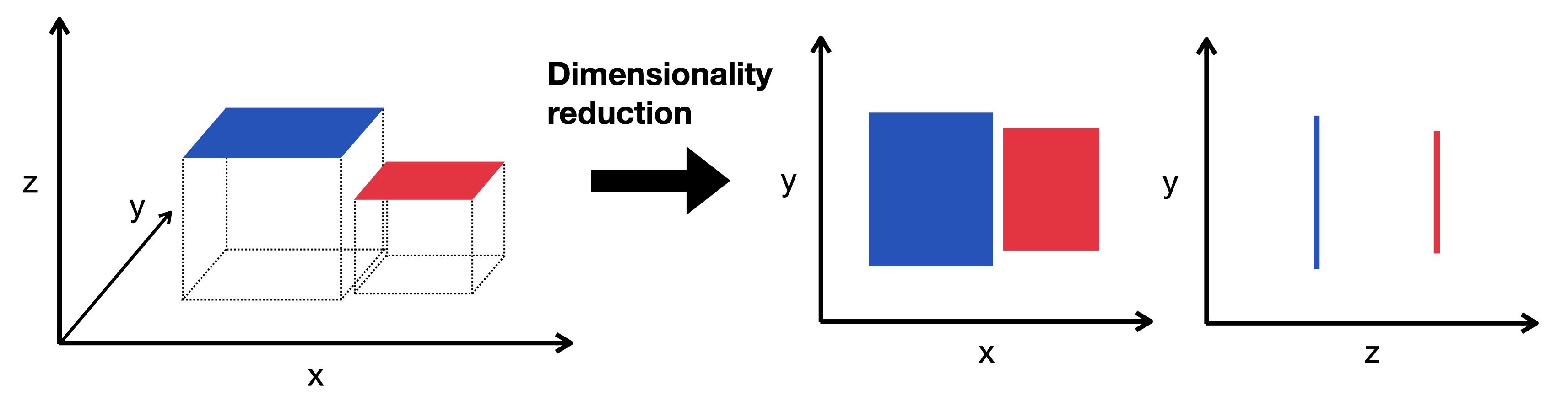
降維（Dimensionality Reduction）技術的主要好處不包含以下哪項？
A
降低儲存空間和計算成本
B
緩解維度災難（Curse of Dimensionality），可能提升模型效能
C
有助於數據視覺化（降到2維或3維）
D
總是能保留原始數據的所有資訊
答案解析
降維是將高維數據映射到低維空間的過程。其好處包括：減少儲存需求和後續模型的計算時間（A）；在高維空間中，數據點變得稀疏，距離度量失去意義，模型容易過擬合，降維有助於緩解這些問題（B）；將數據降至2維或3維可以方便地進行視覺化探索（C）。然而，降維過程（無論是特徵選擇還是特徵提取如PCA）通常會伴隨著資訊損失。雖然目標是盡可能保留重要資訊，但完全保留所有原始資訊通常是不可能的，除非原始數據本身存在完全的線性依賴關係。因此，D 是錯誤的。
#38
★★★
為什麼在模型訓練完成後，評估模型泛化能力時必須使用獨立的測試集，而不是訓練集或驗證集？
A
測試集數據品質通常最高
B
避免資訊洩漏，確保評估結果能客觀反映模型在未見數據上的表現
C
測試集包含的樣本數量最多
D
使用測試集可以加快評估速度
答案解析
模型在訓練過程中直接學習了訓練集的模式，因此在訓練集上的效能通常會偏高。驗證集雖然沒有直接用於訓練模型參數，但它被用於調整超參數和選擇模型結構，模型間接地適應了驗證集的特性。如果在訓練或調參過程中使用的數據上評估最終效能，會導致評估結果過於樂觀（因為模型已經「看過」或「適應」了這些數據），無法代表模型在未來遇到全新數據時的真實表現。獨立的、從未參與任何訓練或調參過程的測試集，才能提供對模型泛化能力的無偏估計。
#39
★★★
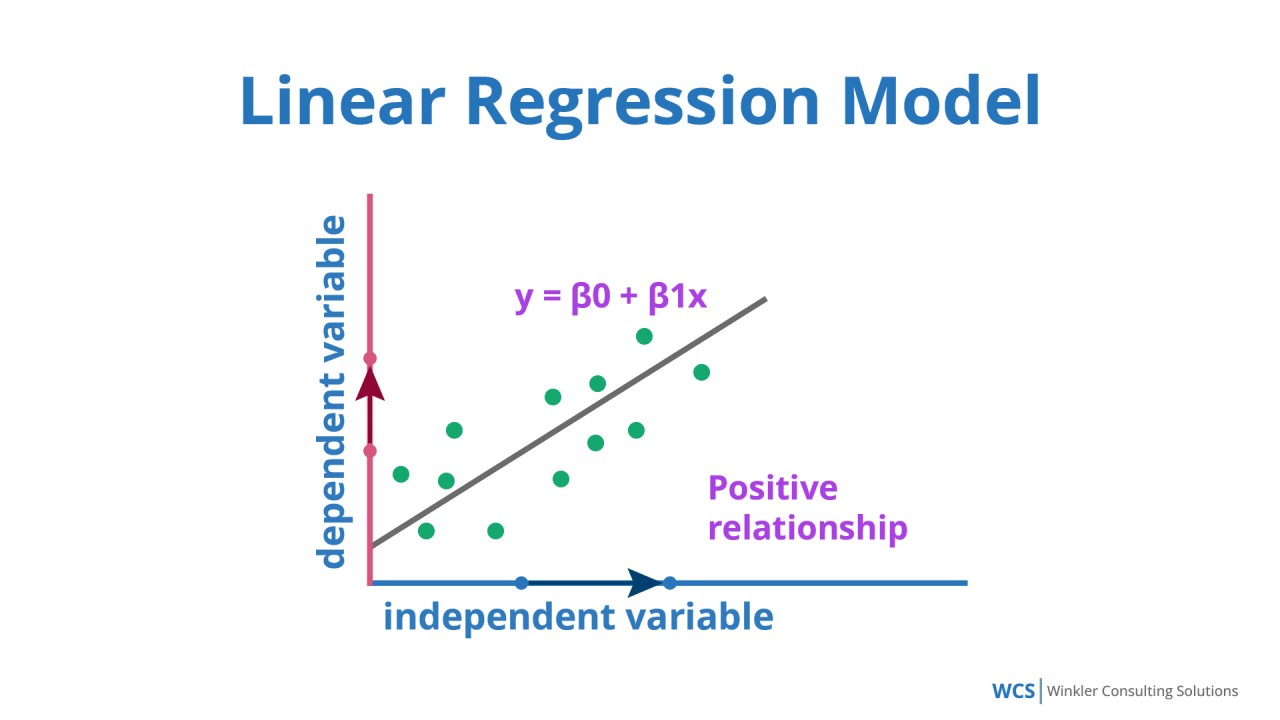
線性回歸（Linear Regression）模型的基本假設不包括？
A
自變數（特徵）與應變數（目標）之間存在線性關係
B
誤差項（Residuals）之間相互獨立
C
誤差項服從常態分佈，且具有相同的變異數（同質性 Homoscedasticity）
D
所有自變數（特徵）之間必須完全不相關
答案解析
線性回歸模型有一些基本假設，違反這些假設可能影響模型的有效性和結果解釋。主要假設包括：線性關係（A）、誤差項獨立性（B）、誤差項常態性與同質性（C）。此外，還假設自變數之間不存在完全共線性（Perfect Multicollinearity），即一個自變數不能是其他自變數的精確線性組合。但它不要求自變數之間必須完全不相關（D），只是高度相關（Multicollinearity）可能導致係數估計不穩定、解釋困難。
#40
★★
在需要同時考慮精確率（Precision）和召回率（Recall）時，除了 F1 分數，還可以參考哪個視覺化工具？
A
直方圖（Histogram）
B
Precision-Recall 曲線（PR 曲線）
C
箱形圖（Box Plot）
D
散點圖（Scatter Plot）
答案解析
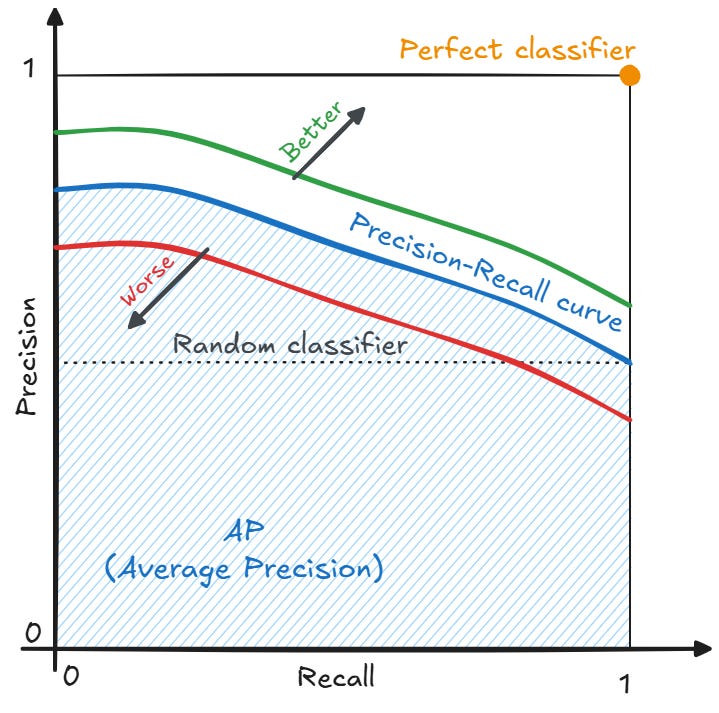
Precision-Recall (PR) 曲線與 ROC 曲線類似，也是透過改變分類閾值來繪製的。不同的是，PR 曲線的橫座標是召回率（Recall），縱座標是精確率（Precision）。PR 曲線對於評估在類別不平衡數據集上的模型效能尤其有用，因為它關注的是正類的預測情況，不像 ROC 曲線會受到大量真負例（True Negatives）的影響。曲線下的面積（Area Under the PR Curve, AUC-PR）也可以作為一個匯總指標。
#41
★★
數據收集過程中，若透過網路爬蟲（Web Scraping）獲取數據，需要特別注意哪個問題？
A
數據量太少
B
網站的 robots.txt 協議、服務條款、以及潛在的法律和版權問題
C
數據格式過於統一
D
數據更新速度太慢
答案解析
網路爬蟲是自動獲取網頁數據的常用技術，但在使用時必須遵守相關規範和法律。網站通常會透過 robots.txt 文件告知爬蟲哪些頁面可以或不可以爬取。此外，網站的服務條款（Terms of Service）可能明確禁止自動爬取。未經授權爬取受版權保護的內容也可能觸法。因此，在進行網路爬取前，務必檢查並遵守這些規則，尊重網站的權利和限制，避免法律風險。
#42
★★
處理數據中的拼寫錯誤或不一致的標籤（例如 "Taipei", "TPE", "台北市"），屬於數據清洗的哪個環節？
A
處理缺失值
B
處理不一致或格式錯誤的數據
C
處理離群值
D
處理重複記錄
答案解析
數據不一致是指同一個實體或概念在數據中以不同的方式表示，或者數據格式不符合預期。例如，同一個城市名稱有多種寫法、日期格式混亂、數值單位不統一等。數據清洗需要識別這些不一致性，並將其標準化為統一的格式或表示方式，以確保數據的準確性和可用性。這通常需要定義轉換規則、使用字典或模糊匹配等技術。
#43
★★
封裝法（Wrapper Methods）進行特徵選擇的主要缺點是？
A
忽略了特徵與模型之間的交互作用
B
計算成本非常高，因為需要反覆訓練模型來評估不同特徵子集
C
只能應用於線性模型
D
無法處理類別型特徵
答案解析
封裝法將特徵選擇看作一個搜索問題。它使用一個特定的機器學習模型作為「黑盒子」，反覆地訓練和評估該模型在不同特徵子集上的效能（如準確率、AUC），並根據評估結果來指導搜索過程（如前向選擇、後向剔除、遞迴特徵消除 RFE），以找到最佳的特徵子集。由於需要為每個候選的特徵子集都訓練和評估一次模型，其計算成本通常遠高於過濾法，特別是在特徵數量較多時。優點是考慮了特徵與特定模型的交互作用，可能找到比過濾法更好的特徵子集。
#44
★★
分層抽樣（Stratified Sampling）在劃分數據集時的主要目的是？
A
確保每個子集（訓練/驗證/測試）的樣本數量完全相等
B
確保每個子集中目標變數（或其他重要變數）的類別比例與原始數據集大致相同
C
完全隨機地抽取樣本
D
加快數據劃分的速度
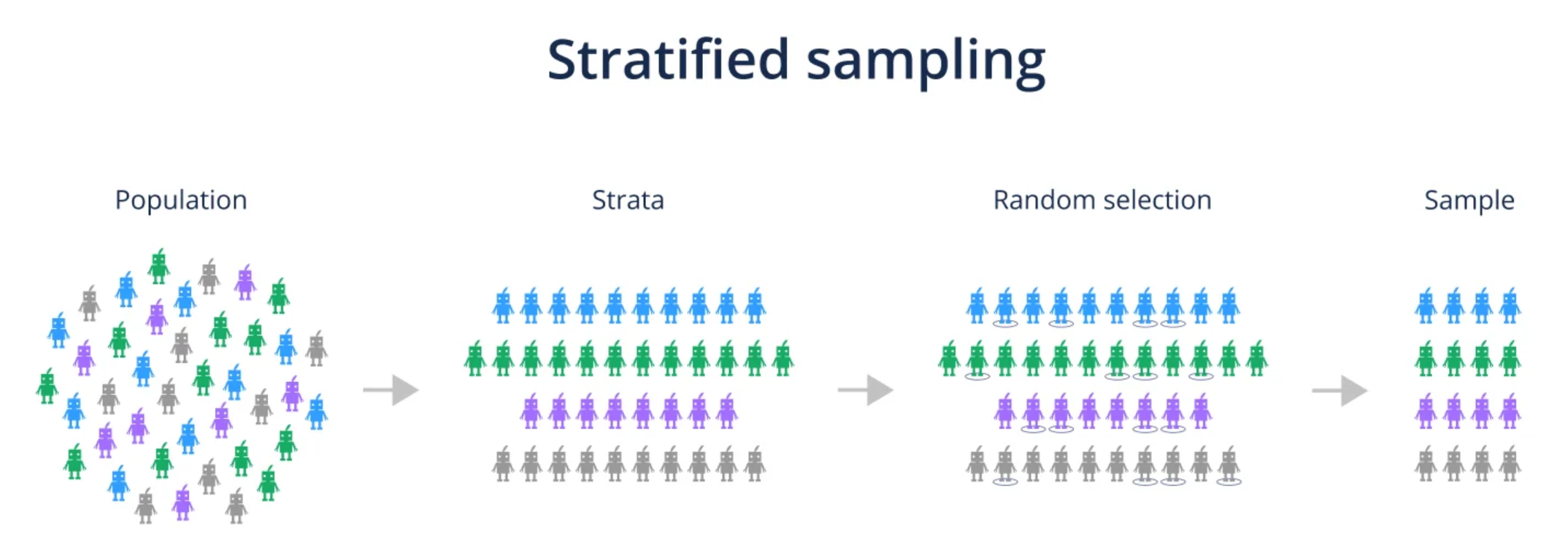
答案解析
在進行隨機劃分時，如果原始數據集中存在類別不平衡或其他重要的分層結構，簡單隨機抽樣可能導致劃分出的子集（特別是較小的驗證集或測試集）中各類別的比例與原始數據相差很大，從而影響模型訓練和評估的代表性。分層抽樣則是在抽樣前先將數據按照目標變數的類別（或其他需要保持比例的變數）分成不同的層（Strata），然後在每個層內部分別按比例進行隨機抽樣。這樣可以確保最終劃分出的訓練集、驗證集和測試集都保持與原始數據相似的類別分佈，使得評估結果更可靠。
#45
★★
支持向量機（SVM）中的「核技巧」（Kernel Trick）主要是用來解決什麼問題？
A
處理缺失值
B
將原始空間中線性不可分的數據映射到更高維的空間，使其可能變得線性可分
C
降低模型的變異（Variance）
D
加速模型的訓練過程
答案解析
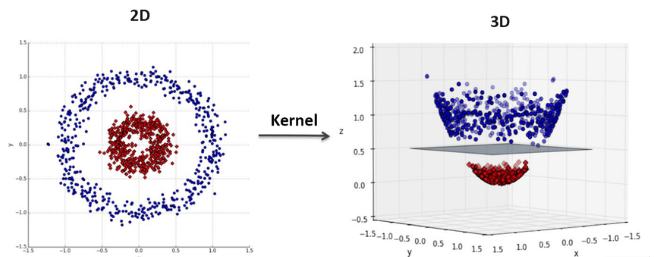
線性 SVM 只能處理線性可分的問題。對於線性不可分的數據，SVM 透過核技巧來實現非線性分類。核技巧的核心思想是：不直接進行高維映射，而是定義一個核函數（Kernel Function，如高斯核 RBF、多項式核），這個函數可以直接計算原始空間中兩個數據點映射到高維特徵空間後的內積（Inner Product），而無需顯式地計算高維空間中的座標。由於 SVM 的優化問題主要依賴於樣本點之間的內積，核技巧使得 SVM 可以在高維甚至無限維的特徵空間中有效地尋找分隔超平面，而計算複雜度僅取決於原始數據的維度和樣本數。
#46
★★
混淆矩陣（Confusion Matrix）可以用來計算哪些分類評估指標？
A
均方誤差（MSE）、平均絕對誤差（MAE）
B
準確率（Accuracy）、精確率（Precision）、召回率（Recall）、F1 分數
C
決定係數（R-squared）
D
模型的訓練時間
答案解析
混淆矩陣是視覺化和總結分類模型預測結果的表格。對於二元分類，它包含四個值：真正例（TP）、假正例（FP）、真負例（TN）和假負例（FN）。基於這四個值，可以計算出多種常用的分類評估指標：
  • 準確率 Accuracy = (TP + TN) / (TP + FP + TN + FN)
  • 精確率 Precision = TP / (TP + FP)
  • 召回率 Recall = TP / (TP + FN)
  • F1 Score = 2 * (Precision * Recall) / (Precision + Recall)
  • 假正例率 FPR = FP / (FP + TN)
等。選項A和C是回歸指標。
#47
★★
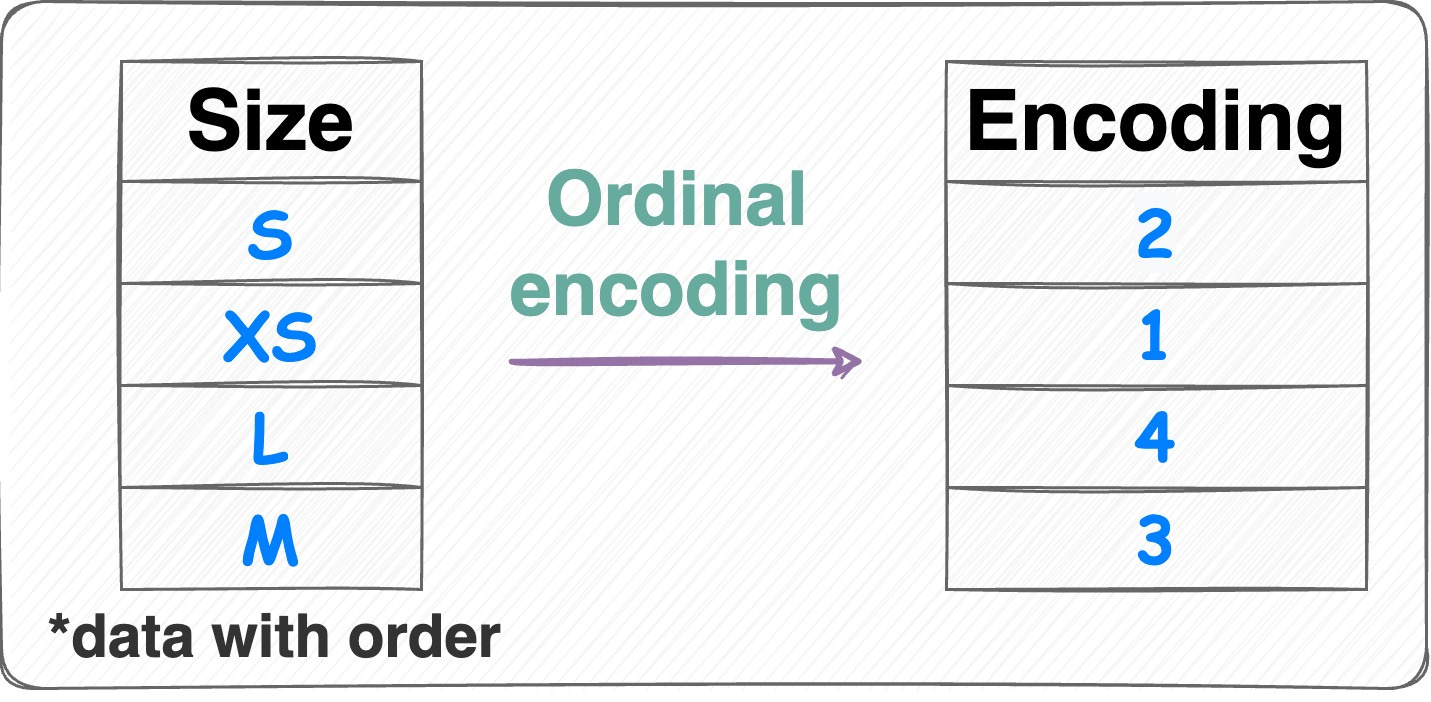
對於順序類別變數（Ordinal Variable），例如「學歷」（國小、國中、高中、大學），使用哪種編碼方式可能比獨熱編碼更合適，因為它能保留順序資訊？
A
獨熱編碼（One-Hot Encoding）
B
標籤編碼（Label Encoding）或序數編碼（Ordinal Encoding）
C
目標編碼（Target Encoding）
D
雜湊編碼（Hashing Encoding）
答案解析
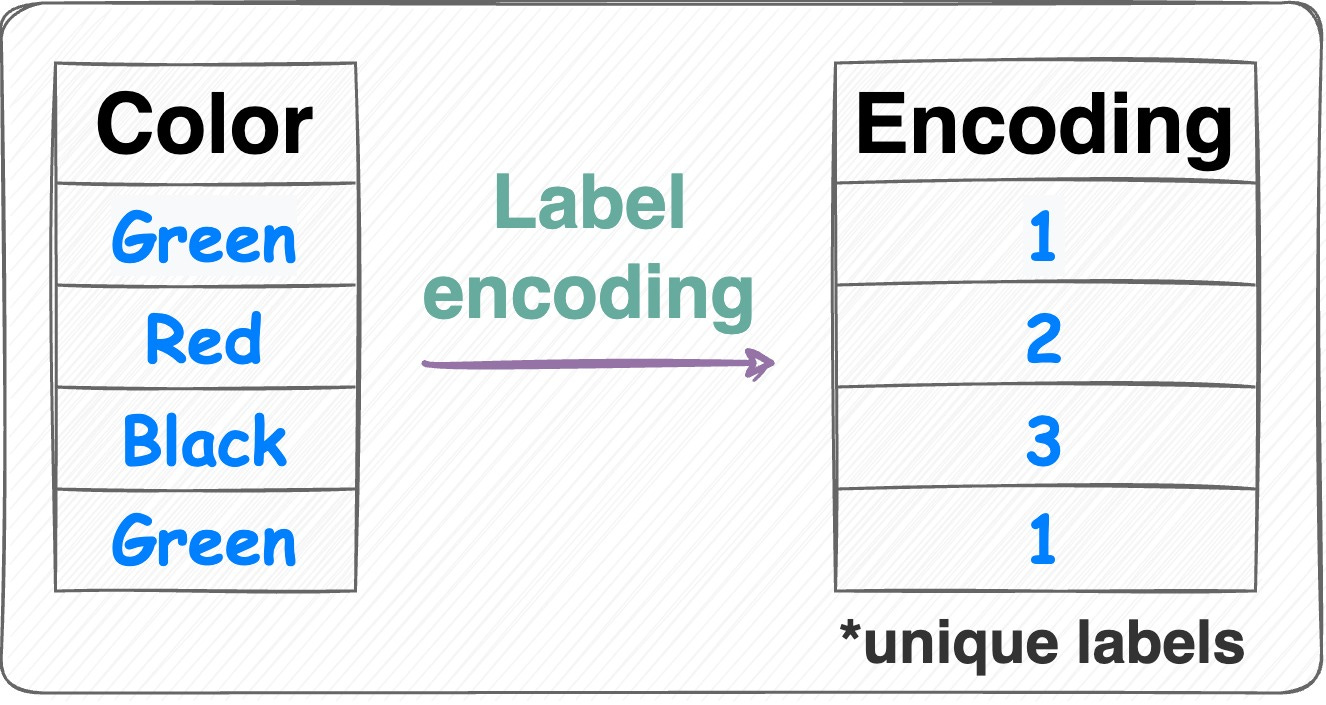
順序類別變數的類別之間存在明確的順序關係（大學 > 高中 > 國中 > 國小）。獨熱編碼會丟失這種順序資訊。標籤編碼（直接將類別映射為 0, 1, 2, 3...）或更明確的序數編碼（Ordinal Encoding，確保映射的數值反映順序）可以保留這種內在的順序關係，對於某些模型（如樹模型）可能更有效。但需要注意，這種數值映射引入了等距假設（例如，大學(3)和高中(2)的差距等於高中(2)和國中(1)的差距），這不一定成立。選擇哪種編碼取決於具體數據和模型。
#48
★★
偏差-變異權衡（Bias-Variance Tradeoff）描述了模型複雜度與哪兩者之間的關係？
A
訓練時間與預測時間
B
模型的偏差（欠擬合風險）與模型的變異（過擬合風險）
C
精確率與召回率
D
數據量與特徵數量
答案解析
偏差-變異權衡是監督學習中的一個核心概念。它指出模型的預期泛化誤差可以分解為偏差的平方、變異以及不可避免的雜訊。通常情況下：
  • 增加模型複雜度會降低偏差（模型擬合能力增強），但會增加變異（模型對訓練數據更敏感，易過擬合）。
  • 降低模型複雜度會增加偏差（模型擬合能力減弱），但會降低變異（模型更穩定）。
目標是找到一個平衡點，使總誤差最小化，即選擇一個複雜度適中的模型，使得偏差和變異都相對較低。
#49
★★
哪種類型的模型通常對數據的縮放（Scaling）最不敏感？
A
K-近鄰（KNN）
B
基於樹的模型（如決策樹、隨機森林、GBDT）
C
支持向量機（SVM）
D
線性回歸 / 邏輯回歸
答案解析
基於樹的模型（如決策樹及其集成模型）在進行節點分裂時，通常是基於單個特徵的閾值來進行的，它關心的是特徵值的相對順序和分割點，而不是特徵的絕對數值大小或尺度。因此，對特徵進行單調變換（如縮放、取對數）通常不會改變樹的結構和預測結果。相比之下，基於距離的模型（KNN、SVM）、基於梯度下降優化的模型（線性回歸、邏輯回歸、神經網路）以及使用正規化項的模型，其效能或收斂速度通常會受到特徵尺度的影響，因此在應用這些模型前進行數據縮放（如標準化）是很重要的預處理步驟。
#50
★★
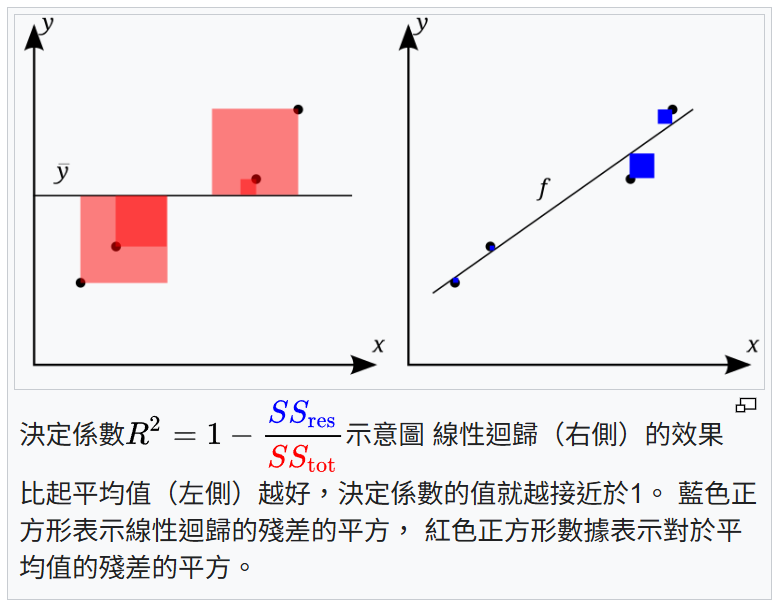
決定係數（Coefficient of Determination, R-squared）在回歸分析中代表什麼？
A
模型預測誤差的平均絕對值
B
模型能夠解釋的應變數（目標變數）總變異量的比例
C
自變數與應變數之間的線性相關程度
D
模型參數估計值的標準誤
答案解析
R-squared 是衡量回歸模型擬合優度的常用指標。它的值介於 0 和 1 之間（理論上可能為負，表示模型比直接預測平均值還差）。R-squared 表示模型所解釋的應變數 y 的總變異量佔應變數本身總變異量的比例。例如，R-squared 為 0.7 表示模型能夠解釋目標變數 70% 的變異性。值越接近 1，表示模型對數據的擬合程度越好。但需要注意，R-squared 會隨著模型中自變數數量的增加而增加（即使增加的變數不相關），因此在比較不同變數數量的模型時，調整後的 R-squared（Adjusted R-squared）可能是更好的指標。選項C描述的是相關係數（Correlation Coefficient）。
沒有找到符合條件的題目。
↑